
- •Геометрия на плоскости и в пространстве.
- •Скалярное произведение.
- •Векторное и смешанное произведение.
- •Уравнение прямой и плоскости в пространстве
- •Евклидово пространство. Скалярное произведение.
- •Изменение матрицы Грама при изменении базиса.
- •Ортогональность.
- •Процесс ортогонализации.
- •Ортогональное дополнение. Ортогональная проекция и составляющая.
- •Геометрический смысл определителя матрицы Грама. Неравенство Адамара.
- •. Расстояния. Псевдорешения. Нормальные решения. Нормальные псевдорешения.
- •Псевдорешения. Метод наименьших квадратов.
- •Нормальное решение
- •Нормальное псевдорешение.
- •Унитарное пространство.
- •Билинейные функции, квадратичные формы.
- •Билинейные формы. Квадратичные формы.
- •Полуторалинейные формы. Эрмитовы формы.
- •Изменение матрицы билинейной (полуторалинейной) формы при изменении базиса.
- •Приведение квадратичных форм (симметричных билинейных форм, эрмитовых форм) к простейшему виду.
- •Метод выделения квадратов (Лагранжа).
- •Приведение квадратичных форм к нормальному виду элементарными преобразованиями
- •Закон инерции квадратичных форм.
- •Теорема Якоби
- •Критерий Сильвестра.
- •Квадрики.
- •Алгебраическая поверхность
- •Уравнение квадрики.
- •Изменение квадрики при аффинном преобразовании
- •Приведение уравнения квадрики к простейшему виду
- •Аффинная классификация кривых второго порядка.
- •Аффинная классификация поверхностей второго порядка
- •Линейный оператор
- •Линейный оператор. Матрица линейного оператора.
- •Примеры линейных операторов.
- •Матрица линейного оператора.
- •Изменение матрицы линейного оператора при изменении базиса.
- •Алгебра линейных операторов.
- •Простейший вид матрицы линейного оператора.
- •Эквивалентность матриц
- •Ранг, дефект линейного оператора.
- •Линейное преобразование
- •Линейное преобразование. Его матрица
- •Изменение матрицы линейного преобразования при изменении базиса.
- •Алгебра линейных преобразований.
- •Инвариантные пространства
- •Собственные векторы и собственные числа. Характеристическое уравнение.
- •Коэффициенты характеристического уравнения. След матрицы.
- •Диагонализируемые преобразования
- •Теорема Шура
- •Сопряженные преобразования.
- •Линейное преобразование и билинейные функции
- •Сопряженное преобразование. Свойства.
- •Нормальное преобразование и его свойства.
- •Ортогональные преобразования
- •Самосопряженное преобразование.
- •Полярное разложение
- •Приведение квадратичных форм
- •Приведение квадратичных форм к главным осям.
- •Приведение пары квадратичных форм
- •Первый способ
- •Пучок матриц
- •Приведение квадрики ортогональным преобразованием. Ортогональные инварианты и полуинварианты.
- •Ортогональная классификация кривых второго порядка
- •Ортогональная классификация поверхностей второго порядка.
- •Аннулирующий многочлен
- •Аннулирующий многочлен вектора.
- •Аннулирующий многочлен подпространства
- •Функции от матриц
- •Вычисление линейных рекуррентных последовательностей
Псевдорешения. Метод наименьших квадратов.
Рассмотрим
несовместную систему линейных уравнений
Ax=b.
Псевдорешением системы линейных
уравнений называется вектор x,
на котором достигается минимум нормы
невязки |Ax-b|.
Задача построения псевдорешения
возникает при подборе параметров
физических процессов. Левая часть
системы уравнений определяется конкретным
видом зависимости от параметров, а
правая – конкретными измерениями.
Поскольку каждое измерение производится
с некоторой точностью, то обычно их
проводят с избытком. В результате
получается несовместная система линейных
уравнений, а задача подбора параметров
сводится к построению псевдорешения.
Сам способ перехода от задачи решения
системы линейных уравнений к нахождению
минимума длины невязки называется метод
наименьших квадратов. Такое название
связано с тем, что
![]() .
.
Обозначим
через W
линейную оболочку столбцов матрицы A.
Задача построения псевдорешения
эквивалентна задаче определения
расстояния от b
до W,
а точнее к
определению проекции b
на W.
Коэффициенты разложения проекции по
столбцам матрицы A
являются решениями системы уравнений
![]() .
Тем самым, задача построения псевдорешения
свелась к решению системы линейных
уравнений.
.
Тем самым, задача построения псевдорешения
свелась к решению системы линейных
уравнений.
Если исходная система имела решение, то оно является также псевдорешением. Необходимым и достаточным условием единственности псевдорешения является условие линейной независимости столбцов матрицы A.
Нормальное решение
В ряде случаев, из множества решений, следует выбрать какое то одно. Нормальным решением системы линейных уравнений Ax=b называется решение наименьшей длины.
Задача отыскания нормального решения сводится к задаче определения расстояния от начала координат до линейного многообразия, заданного системой линейных уравнений Ax=b.
Перпендикуляр,
опущенный из начала координат на это
линейное многообразие, представляется
в виде
![]() линейной комбинации строк матрицыA.
Следовательно, задача построения
нормального решения сводится к решению
системы линейных уравнений
линейной комбинации строк матрицыA.
Следовательно, задача построения
нормального решения сводится к решению
системы линейных уравнений
![]() и вычислению ответа
и вычислению ответа![]() .
.
Нормальное
решение всегда единственно, чего нельзя
сказать о решении системы
![]() .
Необходимым и достаточным условием
единственности решения указанной
системы является условие линейной
независимости строк матрицыA.
.
Необходимым и достаточным условием
единственности решения указанной
системы является условие линейной
независимости строк матрицыA.
Нормальное псевдорешение.
Задача
построения нормального псевдорешения
сводится к решению системы
![]() и вычисления нормального псевдорешения
по формуле
и вычисления нормального псевдорешения
по формуле![]() .
.
Унитарное пространство.
Пусть V линейное пространство над полем комплексных чисел. Можно ли обобщить понятие скалярного произведения на такое пространство. Оказывается, да! Для этого достаточно незначительно изменить аксиомы скалярного произведения.
 .
.
 при
при
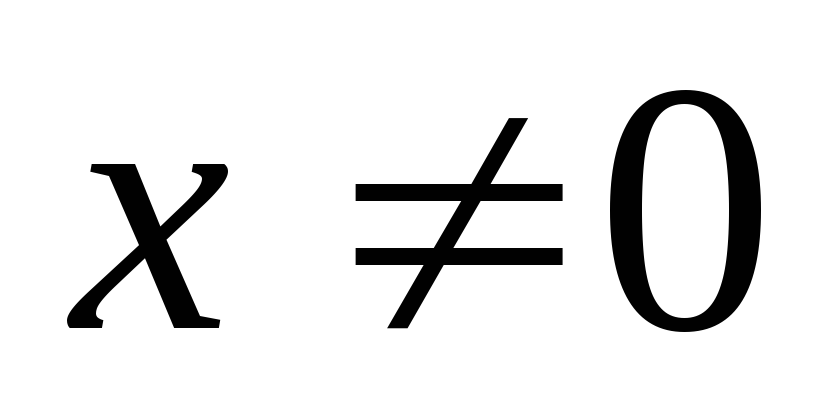 .
.
Черта в свойстве 2 обозначает знак комплексного сопряжения. Пространство над полем комплексных чисел, в котором введено скалярное произведение называется унитарным.
Обозначим
через G
матрицу Грама базисных векторов, то
есть матрицу на пересечении строки i
столбца j
стоит скалярное произведение i-го
и j-го
вектора
![]() .
Используя матричные операции умножения,
получаем
.
Используя матричные операции умножения,
получаем![]() .
Матрицы Грама в разных базисах связаны
формулой
.
Матрицы Грама в разных базисах связаны
формулой![]() ,
гдеP
матрица перехода. Все остальные свойства
скалярного произведения полностью
сохраняются.
,
гдеP
матрица перехода. Все остальные свойства
скалярного произведения полностью
сохраняются.
