
- •Федеральное агентство по образованию
- •Содержание
- •Введение
- •Работа 1. Решение транспортной задачи симплексным методом линейного программирования
- •Задание: используя симплексный метод научиться решать задачи линейного программирования, освоить методику решения одно- и многопродуктовой транспортной задачи в среде Microsoft Office Excel.
- •1.1. Сведение задачи с ограничениями типа неравенств к задаче с ограничениями типа равенств
- •1.2. Симплексный метод решения задачи линейного программирования
- •1.3. Постановка транспортной задачи
- •Алгоритм решения транспортной задачи
- •1.4. Порядок выполнения работы
- •Контрольные вопросы
- •Работа 2. Оптимизация реактора идеального смешения методами нелинейного программирования
- •2.1. Градиентные методы
- •Метод градиента
- •Метод наискорейшего спуска
- •Алгоритм решения задачи методом наискорейшего спуска
- •Блок-схема алгоритма решения задачи методом наискорейшего спуска
- •2.2. Безградиентные методы детерминированного поиска
- •Метод сканирования
- •Алгоритм метода сканирования с переменным шагом
- •Блок – схема алгоритма решения задачи методом сканирования
- •2.3. Методы случайного поиска
- •Метод случайных направлений
- •Метод случайных направлений с обратным шагом
- •Получение случайных чисел из последовательности
- •Алгоритм метода случайных направлений с обратным шагом
- •Блок – схема алгоритма решения задачи методом случайных направлений с обратным шагом
- •2.4. Поиск при наличии «оврагов» целевой функции
- •Алгоритм решения задачи методом шагов по «оврагу»
- •Блок – схема алгоритма решения задачи методом шагов по «оврагу»
- •2.5. Постановка задачи оптимизации реактора идеального смешения
- •2.6. Порядок выполнения работы
- •Контрольные вопросы
- •Работа 3. Оптимизация реактора идеального вытеснения на основе принципа максимума
- •3.1. Формулировка принципа максимума в задаче со свободным правым концом
- •Алгоритм численного решения задачи со свободным правым концом
- •Блок-схема алгоритма решения задачи на основе принципа максимума
- •3.2. Постановка задачи оптимизации реактора идеального вытеснения
- •Приближенные методы численного интегрирования дифференциальных уравнений
- •Метод Рунге-Кутта
- •3.3. Порядок выполнения работы
- •Контрольные вопросы
- •Библиографический список
Алгоритм численного решения задачи со свободным правым концом
Пусть требуется найти
управление ![]() ,
обеспечивающее минимум функционалу
,
обеспечивающее минимум функционалу
![]() (3.11)
(3.11)
и удовлетворяющее системе дифференциальных уравнений
![]() ,
,![]() (3.12)
(3.12)
c начальными условиями
![]() . (3.13)
. (3.13)
Кроме того управление должно удовлетворять ограничениям
![]() , (3.14)
, (3.14)
где ![]() ,
,
![]() ,
,
![]() .
.
Алгоритм решения задачи следующий.
Составляется функция H
![]() , (3.15)
, (3.15)
где ![]() – правая часть j-го
дифференциального уравнения (3.12),
разрешенного относительно первой
производной
– правая часть j-го
дифференциального уравнения (3.12),
разрешенного относительно первой
производной ![]() ,
,![]() – сопряженные функций,
– сопряженные функций, ![]() ,
,![]() .
.
Определяется система сопряженных уравнений
![]() ,
,![]() (3.16)
(3.16)
с конечными условиями
![]() .
.
3. Заданный интервал времени
![]() разбивается на S
частей с шагом
разбивается на S
частей с шагом
![]() .
.
4. Область изменения управления
разбивается на L
частей с шагом
![]() .
.
Решение задачи условимся вести от начала интервала
 .Поэтому в начале интервала
задаются начальные
условия для интегрирования сопряженных
систем уравнений (3.16), полученных в п.
2,
.Поэтому в начале интервала
задаются начальные
условия для интегрирования сопряженных
систем уравнений (3.16), полученных в п.
2,
 ,
, .
.В начале интервала интегрирования
 по известным
по известным
 ,
,
 вычисляется значение
функции Н при каждом значении управления
u
из области
вычисляется значение
функции Н при каждом значении управления
u
из области
 ,
начиная с
,
начиная с до
до
 c
шагом
c
шагом 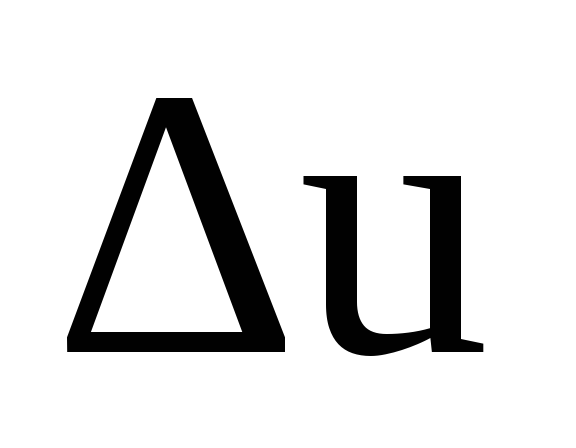 .
.
7. Из рассчитанного массива
значений функции Н
выбирается максимальное и определяется
соответствующее оптимальное управление
![]() .
.
8. На основе
![]() и
и
![]() ,
,![]() рассчитывается для следующего момента
времени
рассчитывается для следующего момента
времени![]() оптимальная фазовая траектория
оптимальная фазовая траектория![]() и значения
сопряженных функций
и значения
сопряженных функций
![]() .
.
9. Используя рассчитанные
![]() ,
,
![]() в исходной (3.12) и
сопряженной (3.16) системах уравнений для
момента времени
в исходной (3.12) и
сопряженной (3.16) системах уравнений для
момента времени
![]() вычисляется функция
вычисляется функция![]() длякаждого управления
u
из области
длякаждого управления
u
из области
![]() также, как это описано
в п. 6 для точки
также, как это описано
в п. 6 для точки
![]() .
.
10. Процедура расчета
повторяется, начиная с п. 6 при каждом
новом значении
![]() до тех пор, пока не
будет рассчитано
управление на всем
интервале времени от
до тех пор, пока не
будет рассчитано
управление на всем
интервале времени от
![]() до
до ![]() .
.
11. В конце интервала
интегрирования необходимо проверить
выполнение конечных условий для функций
![]() :
:
![]() .Если расчетное значение
.Если расчетное значение
![]() ,
то начальные значения
,
то начальные значения
![]() заданы неверно. Требуется изменить
начальные значения так, чтобы конечные
заданы неверно. Требуется изменить
начальные значения так, чтобы конечные
![]() были равны заданным с
допустимой погрешностью
были равны заданным с
допустимой погрешностью
![]() .
При каждом новом значении
.
При каждом новом значении
![]() процедура расчета повторяется,
начиная с п. 5.
процедура расчета повторяется,
начиная с п. 5.
Для определения начальных
значений ![]() предлагается использовать метод
сканирования.
предлагается использовать метод
сканирования.
При использовании данного
метода необходимо задать область
значений начальных условий для
интегрирования сопряженных систем
уравнений
![]() и определить величину рабочего шага
поиска
и определить величину рабочего шага
поиска
![]() .
.
Критерием окончания поиска может служить условие
![]() ,
,
где
![]() – заданная погрешность расчета. Если
в результате поиска не найдено значение
– заданная погрешность расчета. Если
в результате поиска не найдено значение![]() ,
обеспечивающее выполнение условия
окончания поиска, то следует пересмотреть
границы области
,
обеспечивающее выполнение условия
окончания поиска, то следует пересмотреть
границы области![]() либо изменить величину рабочего шага
либо изменить величину рабочего шага![]() .
.
Блок-схема алгоритма решения задачи на основе принципа максимума

3.2. Постановка задачи оптимизации реактора идеального вытеснения
На основе принципа максимума построить оптимальный температурной профиль в реакторе идеального вытеснения.
В реакторе идеального вытеснения протекает реакция первого порядка превращения исходного реагента А в продукт реакции Р.
Скорости химической реакций:
![]() ,
,
![]() ,
,
где ![]() ,
,![]() – константы скорости
реакций, связаны с температурой реакции
уравнением Аррениуса
– константы скорости
реакций, связаны с температурой реакции
уравнением Аррениуса
![]() ,
,![]() ,
,
![]() ,
,![]() – концентрации компонентов А и Р
соответственно.Обозначим
– концентрации компонентов А и Р
соответственно.Обозначим
![]() ,
,
![]() .
.
Процесс реакции в реакторе описывается системой уравнений
![]() ,
,
![]()
с начальными условиями ![]() ,
,![]() ;
;![]() ,
,![]() .
.
Управлением процесса
является распределение температуры
реактора ![]() ,
0С,
которое удовлетворяет ограничениям
,
0С,
которое удовлетворяет ограничениям
![]() ,
где
,
где ![]() ,
,![]() .
.
Время реакции
![]() ,
где
,
где
![]() – время окончания реакции,
– время окончания реакции,
![]() мин.
мин.
Требуется найти такой закон
изменения температуры реактора ![]() ,
при котором концентрация продукта
реакции на выходе реактора максимальна,
что эквивалентно
минимуму функционала
,
при котором концентрация продукта
реакции на выходе реактора максимальна,
что эквивалентно
минимуму функционала
![]() .
.
Шаг разбиения времени
реакции
![]() следует выбрать равным
следует выбрать равным
![]() мин.
мин.
Шаг разбиения области
изменения управления ![]() принять равным
принять равным
![]() 0С.
0С.
Область значений начальных
условий для интегрирования сопряженных
систем уравнений
![]() составляет
составляет
![]() ,
величина рабочего шага поиска
,
величина рабочего шага поиска
![]() .
.
После расчете функции Н
по каждому ![]() в фиксированный момент
времени t
выбирается максимальное значение
функции
в фиксированный момент
времени t
выбирается максимальное значение
функции ![]() ,
при этом величина
,
при этом величина![]() неотрицательна.
Соответствующее этому
значению управление есть оптимальное
управление
неотрицательна.
Соответствующее этому
значению управление есть оптимальное
управление ![]() .
Далее на основе
.
Далее на основе![]() рассчитываются оптимальные
значения концентраций
рассчитываются оптимальные
значения концентраций
![]() и
и![]() ,
а также сопряженных функций
,
а также сопряженных функций![]() ,
,![]() .
.
Расчет ![]() ,
,![]() ,
,![]() и
и![]() в пределах от t
до
в пределах от t
до
![]() осуществляется одним
из приближенных методов
интегрирования дифференциальных
уравнений [7].
осуществляется одним
из приближенных методов
интегрирования дифференциальных
уравнений [7].
