Fundamentals of the Physics of Solids / 13-The Experimental Study of Phonons

13

The Experimental Study of Phonons

As we saw in the previous chapter, the excited states that correspond to the thermal motion of atoms in a crystalline solid can be interpreted in terms of independently generated collective elementary excitations (phonons) governed by the Bose–Einstein statistics. However, only rather indirect, integrated information on the phonon spectrum can be extracted from measurements of thermodynamic, macroscopic properties. In the present chapter we examine some direct methods for studying phonons.

13.1 General Considerations

In addition to giving an account of certain macroscopic properties of crystalline materials, the phonon gas model of lattice vibrations also provides a basis for the interpretation of the behavior of crystals under external influences. For example, when the solid is irradiated with electromagnetic radiation or a beam of particles, the interaction can be visualized as an interaction between the incident particles (quanta) and the gas of phonons. Although the processes that take place inside the system cannot be followed experimentally (the state of the system is not known precisely, therefore even the number of phonons before and after the measurement are unknown to the experimenter), and in many cases the details of the interactions with the phonons are also unknown, nevertheless experiments to measure the inelastic scattering or absorption of the incident radiation by the sample can provide information about the dynamics of the crystal lattice. The reason for this is simple. Consider radiation quanta or particles that are scattered or absorbed, as a result of their interaction with the system, and emit or absorb phonons in the process. By measuring the energy and momentum transferred to the scattered (absorbed) particle, and making use of the conservation of energy and crystal momentum, conclusions can be drawn about the phonon energy – that is, the dispersion relation –, as long as multiple scattering processes can be neglected. This may provide insight into the nature of the forces that hold the crystal together.

430 13 The Experimental Study of Phonons

In principle any particle that interacts with the crystal in one way or another is suitable for such measurements. Without specifying whether photons, electrons, or neutrons are used, the equations for energy and momentum conservation can be written in a general form. We shall denote the particle energy before scattering by εi and the energy of the initial state of the phonon system by

Ei =	ωλ(q) nλ(q) + 21 .	(13.1.1)

q,λ

In the scattering process the energy of the particle may change to εf, and the number of phonons with polarization λ and wave vector q to nλ(q). Because of energy conservation,

εi + ωλ(q)nλ(q) = εf +	ωλ(q)nλ(q) .	(13.1.2)
q,λ	q,λ

At the same time, on account of the discrete translational symmetry of the lattice, momentum conservatio is valid only up to a reciprocal-lattice vector:

pi + q nλ(q) = pf +	q nλ(q) + G ,	(13.1.3)
q,λ	q,λ

where pi and pf are the momenta of the incoming and scattered particles, and G is a reciprocal-lattice vector.

To be able to measure su ciently precisely the energy and momentum transfer to the scattered particle, the energy and momentum of the scattered particle must be of the same order as the energy and quasimomentum of the phonons that are being studied. If one wishes to study the phonons over a relatively broad region of the Brillouin zone, the wavelength of the radiation must be of the order of the lattice constant. It was shown in Chapter 8 on di raction that this part of the electromagnetic spectrum corresponds to X- ray photons.

Typical acoustic phonon energies can be identified with the thermal energy corresponding to the Debye temperature. According to the data listed in Table 12.1, the values of ΘD are on the order of a few hundred kelvins, which corresponds to 10–100 meV. Phonon energies of the same order are obtained for optical phonons if the frequencies in Table 11.3 are converted to energies. This means that acoustic and optical phonon energies are typically a few tens of meV. X-ray photon energies are on the order of a keV, so phonons cause relatively little changes in their energy – therefore very high resolution devices are needed to extract the phonon dispersion relation from inelastic X-ray scattering. The energy of visible photons is around an electronvolt, therefore the issue of energy resolution is not so important. However, the wavelength being much larger than the lattice constant, practically only phonons around q = 0 can be studied. On the other hand, for slow thermal neutrons both energy and momentum are in the suitable range. Before turning to the determination of the phonon dispersion relation through neutron scattering experiments, we examine what information can be extracted from optical measurements.

13.2 Optical Methods in the Study of Phonons

431

13.2 Optical Methods in the Study of Phonons

Although the methods discussed in this section had already been known in the first half of the 20th century, it was only with the advent of highly monochromatic laser sources that the scattering of light became a suitable and widely used method for studying lattice vibrations. This is because even tiny variations of the wavelength of the laser beam are easy to detect, and so su ciently high resolutions can be achieved. A drawback of the method is that the wavelength of visible light ranges from λ = 390 to 750 nm, which corresponds to q 105 cm−1. This is several orders of magnitude smaller than the typical dimensions of Brillouin zones – therefore only phonons close to the center of the Brillouin zone (q ≈ 0) can be studied with this method. The same applies, to an even greater degree, to using infrared radiation with wavelengths in the micron region.

In ionic crystals the electromagnetic field is coupled directly to the charged ions. The explicit form of the Hamiltonian will be given in Chapter 25. Here we shall only make use of the assertion that photons may create and annihilate phonons. In metals and semiconductors the indirect coupling of photons to phonons is more important. The electromagnetic field interacts directly with the highly polarizable and mobile electrons; then, in a second step, these electrons interact with the gas of phonons. We shall analyze these processes in more detail in Volume 2. Throughout the present chapter we shall refer to them as if they were direct interactions between the electromagnetic field and the phonons. We shall ignore the details of the interaction, and impose only the requirements of energy and momentum conservation in all real physical processes in which a photon is absorbed or scattered and a phonon is created or annihilated.

13.2.1 Infrared Absorption

In the simplest interaction between an electromagnetic field and a system described as a phonon gas, one photon of the incident beam is absorbed, and a phonon is created at the same time. As mentioned above, phonon energies are rarely in excess of a few tens of meV. As this is much smaller than the energy of visible photons (a few eV), such photons cannot be absorbed by the crystal via the emission of a single phonon. Because of energy conservation vibrating lattices can absorb only photons in the far infrared, where energies are much lower than in the visible range.

The frequency of the most energetic phonons is of order 1012 Hz. The wavelength of infrared photons of the same frequency is much larger than the lattice constant of crystals, i.e., their wave numbers are negligibly small compared to the dimensions of the Brillouin zone. Such photons can be absorbed only by long-wavelength phonons, with q being practically in the middle of the Brillouin zone, q ≈ 0. Since long-wavelength acoustic phonons do not generate any electric dipole moment, only optical phonons participate in direct

432 13 The Experimental Study of Phonons

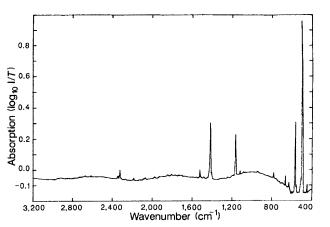
interactions with the radiation field – more precisely, only transverse optical (TO) phonons, since the electric field E is perpendicular to the propagation direction, and so there are no interactions with longitudinal optical phonons. Since optical phonons of wave number q = 0 can be regarded as the internal vibrations of a polyatomic basis, only certain transverse optical phonons may be created in infrared absorption processes – those that correspond to vibrations in which the electric dipole moment is changed. Phonons arising from such processes are called infrared active modes. As mentioned in Chapter 6, the transition matrix elements are subject to selection rules stipulated by the symmetries of the initial and final states. In our case the symmetries of the internal vibrational modes of the basis determine whether or not infrared absorption can occur in a particular mode. Even though the basis contains sixty atoms in fullerite (see page 30), there are only four infrared active optical phonons. There are thus four sharp absorption peaks in the infrared region, as shown in Fig. 13.1.

Fig. 13.1. Infrared absorption spectrum of an approximately	2 μm thick layer
of solid C60 on a silicon substrate, referenced to a clean	silicon substrate
[W. Krätschmer et al., Nature 347, 354 (1990)]

If only direct absorption processes existed, absorption would be observed only at the frequencies of TO phonons. However, due to phonon–phonon interactions, the TO phonon created in the photon absorption process may decay into two phonons or may be scattered by another phonon. These possibilities are shown in Fig. 13.2.

Since the intermediate virtual phonon does not need to obey the law of energy conservation, and only the initial and final states have to be of the same energy, absorption is observed in a finite range of energies. This is illustrated in Fig. 13.3, where the reflectivity of LiGaO2 is plotted in the infrared region.

13.2 Optical Methods in the Study of Phonons

433

Fig. 13.2. Second-order processes, in which the TO phonon created in the photon absorption process splits into two phonons or is scattered by another phonon. Dashed lines represent photons, and wavy lines phonons

At wave numbers associated with certain well-defined frequencies reflectivity drops abruptly, indicating a strong absorption by the sample.

reflectivity (%)

90

80	A1(z)
70	LiGaO2
60
50
40
30
20
10

100

200

300

400

500

600

700

800

% (cm 1)

Fig. 13.3. Variations of the reflectivity of LiGaO2 in the infrared region. The dashed line represents measured data; the solid line is the result calculated from the frequencies of longitudinal and transverse optical phonons [P. Knoll and H. Kuzmany, Phys. Rev. B 29, 2221 (1984)]

13.2.2 Raman Scattering

In the lowest order of interaction, which is linear both in the electromagnetic field and in the ionic displacement, only two processes are possible: the transformation of a photon into a phonon and vice versa. It may occur that the generated phonon decays into two because of the anharmonic terms, and one of the new phonons is then transformed back into a photon. The net result of this process is the transformation of the initial photon into a photon plus a phonon. This can be interpreted as the inelastic scattering of the photon by the lattice, where the energy di erence is carried away by the emitted phonon. Alternatively, the phonon that appears in the first step merges with a thermally excited phonon of the system into a new phonon state, which is then transformed back into a photon. This process can be interpreted as an

434 13 The Experimental Study of Phonons

inelastic photon scattering accompanied by a phonon absorption. A distinction is made between the scattering processes in which an acoustic or optical phonon is involved. The first phenomenon is called Brillouin scattering, and the second Raman scattering.

In Raman scattering1 the emission or absorption of an optical phonon of wave vector q ≈ 0 gives rise to a change in the energy of the incident photon:

ω = ω ωλ(q ≈ 0) .

(13.2.1)

These processes are shown in Fig. 13.4.

Fig. 13.4. Two types of Raman scattering. In Stokes processes a phonon is emitted; in anti-Stokes processes a phonon is absorbed

The change in the photon energy is a direct measure of the energy of the optical phonon. It follows from (13.2.1) that the energy of the scattered phonons may have two values for each phonon branch. The energy of the photon re-emitted in the process with phonon emission is lower than the energy of the incident photon; this is the Stokes component. The process with phonon absorption gives rise to the anti-Stokes component at energies in excess of the incident photon energy. The intensity is temperature dependent for both peaks – but not in the same way. The intensity of the anti-Stokes line is proportional to the number of absorbable phonons. In thermal equilibrium the number of phonons with energy ωλ(q) is given by the Bose–Einstein function

g0(ωλ(q)) =	1	(13.2.2)
	e ωλ(q)/kBT − 1 .

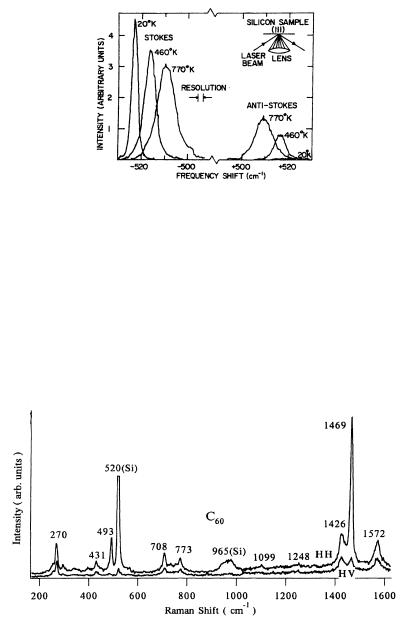
As there are no absorbable phonons at T = 0, the intensity of the antiStokes line vanishes there. The Stokes line is stronger, its intensity is fi- nite even at T = 0, as the phonon emission probability is proportional to g0(ωλ(q)) + 1 on account of stimulated emission processes. This is clearly shown in Fig. 13.5, where the Raman spectrum of silicon is presented at three di erent temperatures.

Just like for infrared absorption, rigorous selection rules – specified by the symmetries of the crystal – determine whether or not a particular phonon

1C. V. Raman, 1928, and independently of him G. Landsberg and F. Mandelstam, 1928. Sir Chandrasekhara Venkata Raman (1888–1970) was awarded the Nobel Prize in 1930 “for his work on the scattering of light and for the discovery of the e ect named after him”.

13.2 Optical Methods in the Study of Phonons

435

Fig. 13.5. Stokes and anti-Stokes components in the Raman spectrum of silicon at three di erent temperatures [T. R. Hart, R. L. Aggarwal and B. Lax, Phys. Rev. B 1, 638 (1970)]

may be created or absorbed via Raman scattering. The general condition for Raman scattering is that the polarizability of the basis must be changed by the optical mode. Phonons that meet this condition are called Raman active modes. Consider, for example, fullerite. Due to the degeneracies that inevitably occur because of the high symmetry, the number of di erent vibrational frequencies at q = 0 is 48 – however only 10 of them are Raman active. These are shown in Fig. 13.6.

Fig. 13.6. Raman spectrum of a thin C60 layer. Two peaks due to the silicon substrate are observed in addition to the ten Raman active modes [P. Zhou et al., Phys. Rev. B 46, 2595 (1992)]

436 13 The Experimental Study of Phonons

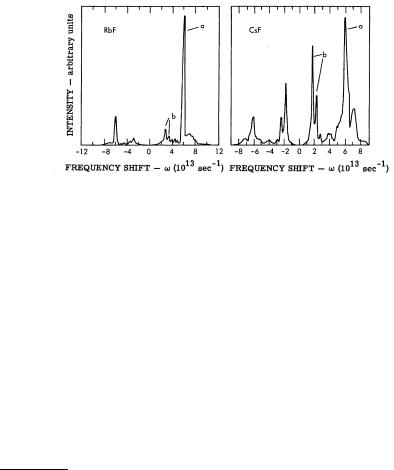
The condition q ≈ 0 can be met not only via the creation or annihilation of a phonon with wave vector q ≈ 0 but also through scattering, in which a higher-order process gives rise to the creation or annihilation of a pair of phonons with opposite wave vectors (q and −q). Since q is arbitrary, and the energy di erence between the scattered and incident photons is now 2 ωλ(q), a smeared-out continuum is obtained rather than a few sharp peaks. Nevertheless the largest contribution comes from the region where the density of states is high – that is, from optical phonons and high-energy acoustic phonons. This process is called the two-phonon Raman scattering. As it is a higher-order process, it could be expected to be less intense than one-phonon scattering, however, this can be compensated for by the high density of states of phonons at the boundary of the Brillouin zone. Figure 13.7 shows the calculated second-order Raman spectra for two alkali halide crystals.

Fig. 13.7. Calculated second-order Raman spectra for two alkali halide crystals [J. R. Hardy and A. M. Karo, Proc. of the Int. Conf. on Light Scattering Spectra of Solids, New York, p. 99 (1968)]

13.2.3 Brillouin Scattering

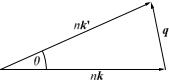
The interpretation of Brillouin scattering2 in terms of acoustic phonons is based on the conservation of energy (13.2.1) and crystal momentum; however, in contrast to Raman scattering, the change in the photon momentum cannot be neglected. It should be borne in mind that momentum conservation implies that the wave vector of the incident photon is changed – no matter how small the wave number of the emitted or absorbed phonon. Upon its penetration into a sample of refractive index n, the propagation velocity and thereby the wave number of the incident light is changed, the momentum associated with the photon is nk. Momentum conservation then takes the form

2 L. Brillouin, 1922.

13.2	Optical Methods in the Study of Phonons		437
nk	= nk ± (q + G) .	(13.2.3)

As it has been mentioned, the wave number |k| of photons is much smaller than the dimensions of the Brillouin zone, hence the previous equation can be satisfied only by the reciprocal-lattice vector G = 0.

As the energies of visible photons and acoustic phonons are very di erent, on the order of 1 eV and 1–10 meV, respectively, there is hardly any change in the energy and the magnitude of the wave vector of the photon – however, the direction of the latter undergoes an observable change. We shall denote the angle between the propagation direction of the incident and scattered photons by θ; the vector triangle that illustrates momentum conservation is shown in Fig. 13.8.

Fig. 13.8. The wave vector of the incident and scattered photons in Brillouin scattering

To a good approximation, the wave number of the emitted or absorbed phonon is

q = 2n k sin			θ				(13.2.4)
					.
			2
In terms of the photon frequency,
q =	2n ω	sin		θ			(13.2.5)
						.
	c			2

In the long-wavelength region, which can be probed by Brillouin scattering, phonons of polarization λ propagate with the sound velocity cλ. Since the phonon energy is the same as the change in the photon energy, we get

ω = cλq = cλ	2n ω	sin	θ		(13.2.6)
				.
	c		2

When the intensity distribution of the scattered beam is measured as a function of energy in a fixed direction close to the direct beam, weaker peaks are observed on both sides of the large elastic peak, as shown in Fig. 13.9. They correspond to the emission and absorption of longitudinal and transverse phonons. The group velocities of the branches can be determined from the shift of the peaks relative to the direct beam.

438 13 The Experimental Study of Phonons

Fig. 13.9. Brillouin spectra of two single crystals of neon of di erent orientations, along a direction close to that of the direct beam [B. P. Stoicho et al., Proc. of the 2nd Int. Conf. on Light Scattering in Solids, Paris, p. 450 (1971)]

13.3 Neutron Scattering on a Thermally Vibrating Crystal

In optical measurements only phonons at the center of the Brillouin zone (q ≈ 0) can be studied, since energy and momentum conservation can be satisfied only here on account of the great disparity between phonon and photon propagation velocities. The situation is di erent for neutrons. By rearranging (8.2.2), the formula relating the wave number and energy of the neutron we get

ε = 2.1

k[Å−1] 2

× 10−3 eV .

(13.3.1)

The energy of neutrons with a de Broglie wavelength of λ ≈ 1 Å is about 0.1 eV. Expressed as a thermal energy in kelvins,

ε/kB = 24

k[Å−1] 2

K .

(13.3.2)

Since the dimensions of a typical primitive cell are on the order of a few Å, the magnitude of the wave vector of the excitations (phonons) is typically on the order of a few Å−1. The wave number of neutrons is in the same range if their thermal energy corresponds to about 100 K. Such so-called thermal neutrons are thus just in the ideal energy and wave-number range for inelastic scattering. Moreover, neutrons interact directly with nuclei, and – through magnetic interactions – with the electron cloud when the latter possesses a magnetic moment. Therefore thermal neutrons provide an almost ideal probe to study lattice vibrations and magnetic excitations in solids.3

3Bertram Neville Brockhouse (1918–2003) and Clifford Glenwood Shull (1915–2001) shared the Nobel prize in 1994 “for the development of neutron