Fundamentals of the Physics of Solids / 06-Consequences of Symmetries

6.2 Consequences of Translational Symmetry

191

is related to symmetries. As will be demonstrated later, the energy spectrum of states characterized by the wave vector k displays the same symmetries as the crystal itself. On the other hand, as it has been mentioned, the primitive cell spanned by the primitive vectors does not usually exhibit the symmetries of the crystal, whereas the Brillouin zone does (similarly to the Wigner–Seitz cell of the direct lattice). Thus the symmetries of the energy spectrum are more transparent when the latter is represented in the Brillouin zone.

6.2.4 Conservation of Crystal Momentum

Noether’s theorem9 establishes that invariance under symmetry transformations usually implies conservation laws. Spatial translations are related to momentum conservation; time translations to energy conservation; rotational symmetry to angular-momentum conservation; and gauge symmetry to charge conservation.

Crystalline systems are not invariant under arbitrary translations, therefore, strictly speaking, momentum is not conserved. However, as mentioned above, because of discrete translational symmetry, crystalline states may be characterized by a wave vector k, and the quantity k plays a role similar to momentum. We shall prove that although no strict conservation law is valid for k, discrete symmetries nevertheless imply a conservation law of rather limited validity. For this reason the crystal momentum k is often called the quasimomentum; the same name is often applied to k itself in the literature.

In quantum mechanics, the time derivative of the translation operator is given by

dO(tn)		=	i	[H, O(tn)] .	(6.2.30)
dt

Since the Hamiltonian commutes with the translation operator in crystalline systems, we have

	dO(tn)		= 0 .	(6.2.31)
	dt

Consequently, the wave vector k that characterizes the transformation of the wavefunction under translations is independent of time.

Suppose that the wavefunction of the system can be written as the product of the wavefunctions of r subsystems,

ψk = φk1 φk2 . . . φkr ,

(6.2.32)

where the behavior of the subsystems under translations is characterized by a set of wave vectors kl (quasimomenta kl), that is,

O(tn)φkl (r) = e−ikl ·tn φkl (r) .

(6.2.33)

Then the behavior of the whole system under translations is governed by

9 E. Noether, 1918.

192 6 Consequences of Symmetries

O(tn)ψk(r) = e−ik·tn ψk (r) ,

(6.2.34)

where the wave vector k of the whole system is the sum of the wave vectors of its subsystems:

r
k = kl .	(6.2.35)

l=1

This is true even if the complete wavefunction of the system has to be constructed as the symmetrized or antisymmetrized product of the wavefunctions of the subsystems.

Microscopic processes that occur in the crystal – e.g., collisions between electrons – may change the wavefunctions,10 and thus the quasimomenta of the subsystems. Assume that, as a result of such an internal collision, the initial state

	ψk = φk1 φk2 . . . φkr				(6.2.36)
of the system changes into the final state
ψk = φk1 φk2		. . . φkr ,			(6.2.37)
where	r		r
		k		kl .
k =	kl ,		=		(6.2.38)
	l=1		l=1

If the system is not subject to any external perturbation, then constancy of k in time means

k ≡ k .

(6.2.39)

Instead of equality – which would rigorously hold for continuous translational symmetry – only the equivalence (≡) of the initial and final wave vectors is guaranteed by discrete translational symmetry, that is, the two may di er by a reciprocal-lattice vector:

k = k + G .

(6.2.40)

This is because only the phase factors that appear in the wavefunctions have to be equal – that is, for a translation through an arbitrary lattice vector tn only the equality

e−ik·tn = e−ik ·tn

(6.2.41)

is required. This is also met by equivalent wave vectors.

In vacuum, electrons interact via Coulomb repulsion. The situation is more complicated in solids. As we shall see in Volume 3, the e ects of other electrons can be taken into account using some kind of modified, e ective interaction between electrons. However, just like Coulomb interaction, this e ective interaction is a pair interaction: it leads to elementary processes in which the state of only two electrons change at the same time. To put it otherwise: in an elementary process two electrons with quasimomenta k1 and k2 are scattered into a state with quasimomenta k1 and k2. This scattering process is illustrated in Fig. 6.5.

10 Note that even in thermal equilibrium the system is not in a pure state.

6.2	Consequences of Translational Symmetry	193
k1	k'1
k2	k'2

Fig. 6.5. Diagrammatic representation of the interaction between two electrons, with the initial and final wave vectors of the particles

Strict momentum conservation applies to all scattering processes among free electrons. According to the foregoing, this requirement is replaced by

k1 + k2 = k1 + k2 + G

(6.2.42)

for electrons moving in a crystal lattice.

The interaction of electrons with lattice vibrations may be interpreted in terms of the creation (emission) and annihilation (absorption) of a quantum of lattice vibration – a phonon. Such processes are shown in Fig. 6.6, where solid lines represent electrons and wavy lines the quanta of lattice vibrations emitted or absorbed in the interaction.

q	q
k' = k+q	k
k	k' = k-q

Fig. 6.6. Diagrammatic representation of the emission and absorption of quanta of lattice vibrations by electrons. Solid lines are electrons, wavy lines are lattice vibrations

In a process where a single electron absorbs a phonon of wave vector q, the electron is scattered into a state with wave vector

k = k + q + G .

(6.2.43)

In processes where phonons are emitted

k + q = k + G .

(6.2.44)

Processes in which G = 0 are called normal processes (N-processes), while those in which G = 0 are called umklapp processes (U-processes).11 This distinction is important because normal and umklapp processes may give essentially di erent contributions to the macroscopic properties of the crystal. For

11R. E. Peierls, 1929. The English equivalent of umklapp process is flip-over process, however this is hardly used in the literature.

194 6 Consequences of Symmetries

example, thermal conductivity cannot be understood without taking umklapp processes into account. On the other hand, there are some physical properties of solids that may be interpreted without recourse to the discreteness of the lattice. When the lattice model of a crystal is replaced by a continuous one, the size of the primitive cell goes to zero, and the vectors of the reciprocal lattice become infinitely large. Umklapp processes are then negligible, and strict momentum conservation is recovered.

The conservation of quasimomentum may be applied to the scattering of an incident beam of photons, neutrons, or electrons by crystalline samples. Assume that the incident beam is described by a plane wave, i.e., the incoming particles have a well-defined momentum (or wave number). Due to the discrete translational symmetry of the sample, the initial wave vector k of the incoming particle may change by a reciprocal-lattice vector in elastic scattering processes – i.e, when the state of the sample does not change. Thus the outgoing beam is made up of particles with wave vector

k = k + G , |k | = |k|

(6.2.45)

or momentum k . As we shall see in Chapter 8, this constraint is just the

Laue condition of di raction.

In inelastic processes a quantum of lattice vibration of wave vector q may be created or absorbed in the interaction between the incoming particles and

the solid. Then condition
k = k + q + G	(6.2.46)
needs to be satisfied in processes with phonon emission and
k = k − q + G	(6.2.47)

in processes with phonon absorption. The conservation of quasimomentum can be written similarly for other processes, e.g., scattering or absorption of light (photons) by a system of electrons.

The foregoing discussion applies to perfect crystals that are free of impurities and defects. Such imperfections are always present in real crystals, nevertheless as long as their concentration is low, the probability that scattering occurs on them is negligible, and so the above selection rules can be used. Because of the periodic boundary condition, the above considerations are valid for states within the sample, far from its surface. In processes where scattering occurs on surface states, only the component of the wave vector parallel to the surface (k ) is conserved, the perpendicular component (k ) is not.

6.2.5 Symmetry Properties of Energy Eigenstates

As we have seen above, microscopic states within a crystalline material can be characterized by the wave vector k. However, nothing has been said of the

6.2 Consequences of Translational Symmetry

195

energy εk of the states yet. We shall show that whatever the explicit form of the Hamiltonian, the symmetry properties of the system appear in εk, too.

Suppose that a solution to the Schrödinger equation

Hψk(r) = εkψk (r)

(6.2.48)

is known. This may be an electronic state, a vibrational state of the lattice, or a magnetic excitation. Let us now examine what happens when this state is acted upon by a symmetry element of the space group of the crystal, {α|tn}, which is composed of a rotation α and a translation tn.

If the system is not subject to any external perturbation, then the symmetry elements of the space group of the crystal leave the Hamiltonian invariant, and it commutes with these symmetry operations, that is,

O({α|tn})H = HO({α|tn}) .

(6.2.49)

Acting on the Schrödinger equation (6.2.48) with the symmetry operator and using the previous commutation relation we have

HO({α|tn})ψk (r) = εkO({α|tn})ψk (r) .

(6.2.50)

Apparently, in addition to ψk (r), O({α|tn})ψk (r) is also an eigenfunction of the Schrödinger equation, with the same energy eigenvalue εk. Had we made recourse to Wigner’s theorem, we could have written down this result immediately.

Now let us examine the behavior of the wavefunction O({α|tn})ψk (r) under translations – in particular, the action of the translation operator O(tm) = O({E|tm}) on this state. Using the relation

O({E|tm})O({α|tn}) = O({α|tn})O({E|α−1tm}) ,

(6.2.51)

which is a straightforward consequence of the multiplication rule for the elements of the space group, we have

O(tm)O({α|tn})ψk(r) = O({α|tn})O(α−1 tm)ψk (r)

= O({α|tn})e−ik·(α−1tm )ψk (r)

(6.2.52)

=O({α|tn})e−i(αk)·tm ψk(r)

=e−i(αk)·tm O({α|tn})ψk(r) .

The wave vector of the transformed wavefunction is thus αk. However, as the energy of the state remains the same, we have

εαk = εk .

(6.2.53)

It can be established in complete generality that εk possesses the full symmetry of the point group.12

12Note that in this derivation we did not have to assume that tn in {α|tn} is a translation vector of the lattice, thus our result is also valid in the case when the space group contains glide reflections and/or screw rotations.

196 6 Consequences of Symmetries

In later chapters dealing with electrons, phonons, and magnons, one of our most important tasks will be the determination of the energy εk for all possible values of k – as this provides the dispersion relation of the excitation. By exploiting the symmetries of εk, the energy values do not need to be determined for each point of the full Brillouin zone separately: calculations or measurements can be restricted to a small portion of the zone. Energies for any other k can then be established using symmetry considerations.

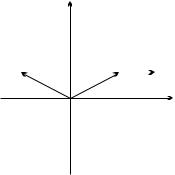
Fig. 6.7. Wave vectors with the same energy in the Brillouin zone of a twodimensional square lattice

Figure 6.7 clearly shows that in a two-dimensional square crystal calculations have to be performed in one-eighth of the Brillouin zone, as symmetry operations relate any general point k = (kx, ky ) to seven others. In a threedimensional cubic crystal a general point (kx, ky , kz ) of the Brillouin zone is related to 47 others by the 48 symmetry operations of a cube, as it can be read o from Tables 5.1 and 5.4. Thus in this case the spectrum needs to be determined on 1/48 of the Brillouin zone.

Next, let us consider crystals with inversion centers. Inversion transforms the variable r into −r, and a state with wave vector k into another with wave vector −k. However, because of its axial vector character spin is left invariant, and so

εk,σ = ε−k,σ

(6.2.54)

For spinless excitations – e.g., excitations of lattice vibrations – the relation

εk = ε−k

(6.2.55)

is valid more generally, even in crystals without an inversion center. This is the consequence of invariance under time reversal, as in this particular case time reversal is equivalent to complex conjugation. By taking the complex conjugate (cc) of the Schrödinger equation, and using the Hermiticity of the Hamiltonian,

	(r) = ε	k	ψ	(r) .	(6.2.56)
Hψk			k

6.2 Consequences of Translational Symmetry

197

The transformation properties of wavefunctions under translations imply that complex conjugation of the wavefunction takes a state with quasimomentum k into one with quasimomentum −k. This means that for spinless excitations the excitation energy is always an even function of the wave number.

The situation is more complicated for electrons. If spin–orbit interactions are taken into account but no magnetic field is present then the Hamiltonian

H = −	2		2 + U (r) +			1 dU (r)			(r × p) · s ,	(6.2.57)
	2m	e		2m2c2		r		dr
				e

which contains the term given in (3.1.33), is invariant under time reversal. Therefore the time reversed of each eigenfunction is also an eigenfunction, with the same energy. However, the presence of spin–orbit interaction no longer permits us to index the eigenstates with the spin z component: the latter is not a good quantum number any more. Time reversal changes the sign of orbital angular momentum and spin alike: p → −p and s → −s. The eigenstates ψk,α(r) and ψk,β (r) of the Hamiltonian can therefore be written as linear combinations of the ms = ±21 states |↑ and |↓ :

ψk,α(r) = χk,+(r)|↑ + χk,−(r)|↓ ,

(6.2.58)

ψk,β (r) = −χk,−(r)|↑ + χk,+(r)|↓ .

These states may be chosen such that ψk,α(r) go over into ψk,↑(r) and ψk,β (r) into ψk,↓(r) when the strength of the spin–orbit interaction vanishes.

Instead of (6.1.23), the time reversal operator may be written as

T = e−iπsy K0 = −iσyK0 ,

(6.2.59)

which amounts to a di erent choice of the phase factor. When applied to the above states,

T ψk,α(r) = ψ−k,β (r) and T ψk,β (r) = −ψ−k,α(r) ,

(6.2.60)

which leads to

εk,α = ε−k,β ,

εk,β = ε−k,α .

(6.2.61)

Owing to the spin–orbit interaction, the two spin states associated with the same wave vector k have di erent energies, however for each of them there exists another state with the same energy. This is just Kramers’ theorem for one-particle electron states.

If the crystal has inversion symmetry in addition to time reversal invariance then relations (6.2.54) and (6.2.61) imply

εk,α = εk,β

(6.2.62)

as well, that is, in the absence of an external magnetic field electron states show spin degeneracy, despite the explicit spin-dependence of the spin–orbit interaction. This degeneracy is lifted when inversion symmetry is broken.

198 6 Consequences of Symmetries

In certain cases states that correspond to ks on the boundary of the Brillouin zone have special properties: for certain symmetries the derivative of the dispersion curve – that is, the velocity of the particle associated with the excited state – vanishes. In the customary representation this means that dispersion curves arrive perpendicularly at the boundaries of the Brillouin zone. We shall investigate the conditions for this.

Suppose that one of the boundary planes of the Brillouin zone is transformed by a reflection symmetry of the crystal into another plane whose points are equivalent with those of the original plane – that is, the two plane faces can be transformed into one another by a translation through a reciprocallattice vector G. This also means that this boundary is itself a mirror plane of the reciprocal lattice.

Consider a point k1 close to the boundary of the Brillouin zone, as shown in sectional view in Fig. 6.8. If reflection symmetry takes k1 into k2, the corresponding energies are equal: εk1 = εk2 . Translation of k2 through a reciprocal-lattice vector G gives k3. Because of the equivalence of these points εk3 = εk2 , and so εk1 = εk3 .

			ky
			/a
			G
					k3
		k2	k1
/a				/a kx

/a

Fig. 6.8. Wave vectors that are transformed into one another by a reflection or a translation through a reciprocal-lattice vector

Unless the energy level becomes degenerate with another, the relation εk1 = εk3 implies that as k moves along a line perpendicular to the zone boundary εk takes an extremum on the boundary. This implies that the dispersion curve is perpendicular to the boundary, i.e., its normal derivative – the velocity of the excitations – vanishes.

This requires that this piece of the zone boundary be a symmetry plane – and also that degeneracies be lifted on the boundary. If the latter requirement is not met, the previous relations imply that the derivatives of the dispersion curve are equal in magnitude but opposite in sign in the two branches. We shall see an example in the band structure of silicon and germanium.

6.3 Symmetry Breaking and Its Consequences

199

6.3 Symmetry Breaking and Its Consequences

In the foregoing we have dealt mostly with the symmetries that appear in crystalline systems and emphasized their importance in describing physical properties. We have not investigated how this symmetry is related to the full symmetry of the system’s Hamiltonian. Later, when the Hamiltonian – of the system of electrons or the lattice itself – is specified, we shall see that it possesses more symmetries than the actual physical state. The Hamiltonian is invariant under an arbitrary translation, while the crystal itself only under discrete ones. In such cases some symmetry of the Hamiltonian is said to be spontaneously broken in the physical system. Just as the presence of symmetries helps to understand the behavior of the physical system, their absence, i.e., the breaking of some symmetries of the Hamiltonian may also have important implications. Symmetry breaking may also occur when a system undergoes a transition from one phase to another. In this case symmetry considerations may be helpful in describing some features of the transition and of the new phase.

6.3.1 Symmetry Breaking in Phase Transitions

The crystalline phase, which is invariant under discrete translational symmetries, is reached through a phase transition from the liquid phase, which is invariant under arbitrary translations. Further phase transitions may occur in the crystalline state; for example, di erent modifications may become stable, or a magnetic or superconducting phase may appear below a certain critical temperature. In each of them, further symmetries are broken. Whether the transition itself is firstor second-order, symmetry is always broken abruptly. This is expressed by Landau’s statement, which P. W. Anderson called the first theorem of condensed-matter physics: Symmetry cannot change continuously. A system is either invariant or not under a symmetry operation. However small the symmetry-breaking contribution in a physical quantity, if it is finite the symmetry is broken.

It should be noted that phase transition is not necessarily accompanied by a change in symmetry. A typical example for this is the transition between liquid and gas phases. However, here we are interested in the general conclusions that can be drawn from symmetry considerations provided symmetry is changed.

The basic assumption underlying the Landau theory of phase transitions13 is that in second-order (continuous) phase transitions the phase that is stable at lower temperatures is always distinguished from the high-temperature disordered phase by a suitable order parameter. This order parameter vanishes in the disordered (usually higher-temperature) phase and appears continuously in the phase transition, which is why free energy can be expanded in its powers. We shall present a somewhat more detailed discussion in Chapter 14 in the

13 L. D. Landau, 1937.

200 6 Consequences of Symmetries

context of phase transitions of magnetic systems. As E. M. Lifshitz pointed out in 1941, the method provides a means to investigate which symmetries of a particular crystal might be preserved. For example, in an alloy undergoing disorder–order phase transition one may predict which sites of the crystal will be occupied by one atomic species and which sites by the other. Even more interesting is that when magnetic ordering takes place, knowledge of the symmetries of the high-temperature magnetically disordered phase permits one to predict the symmetries of the magnetically ordered states that might appear

– provided the phase transition is of second order.

6.3.2 Goldstone’s Theorem

The above considerations are concerned with the macroscopic properties that a state arising from symmetry breaking might have. Conversely, Goldstone’s theorem14 is concerned with the system’s microscopic behavior. Here we give the statement without proof: If the Hamiltonian of a system possesses some continuous symmetry that is broken in the actual physical state then – provided the interaction is not long-ranged – the energy of the lowest-lying excited states of the system are on the order of 1/N above that of the ground-state. In the N → ∞ limit the energies of the excited states form a continuum, which is not separated by any gap from the ground state. Moreover, this continuum is similar to the energy spectrum of a system of free particles obeying Bose– Einstein statistics.

The low-lying excited states arise from the fluctuations of the symmetrybreaking order parameter. According to the theorem the spectrum of these fluctuations can be interpreted in terms of bosonic e ective particles, elementary excitations. These soft modes are called Goldstone bosons. The energy of the excitations is proportional to their wave number, except when the order parameter is a conserved quantity; in this case the energy is proportional to the square of the wave number.

We shall see an example for this in lattices held together by short-range forces, where breaking the continuous translational symmetry gives rise to low-energy long-wavelength acoustic phonon modes. Similarly, breaking the continuous rotational symmetry in isotropic ferroor antiferromagnetic materials leads to low-energy spin waves. In both cases the spectrum of collective excitations is gapless. Note that the theorem states nothing about breaking a discrete symmetry of the Hamiltonian. In this case the ground state is usually separated from the continuum of excited states by a finite gap.

It is essential that Goldstone bosons do not appear for long-range forces: the spectrum of collective bosonic excitations has a gap then. When examining the excitation spectrum of an interacting electron gas we shall see that plasmons have a finite energy as Coulomb repulsion has a long range. In Wigner crystals (to be discussed in Chapter 30) two soft transverse modes appear,

14 J. Goldstone, 1961.