Fundamentals of the Physics of Solids / 07-The Structure of Crystals

7

The Structure of Crystals

As we shall illustrate with several examples below, the knowledge of the space group (the geometrical symmetries of the crystal) is not su cient to reconstruct the structure of the crystal – i.e., the position of the atoms in the primitive cell – unambiguously. Di erent ways of decorating the primitive cell may lead to the same space group. This means that the number of structure types is expected to be much higher than the number of space groups.

The structure of naturally occurring crystals shows a remarkable diversity indeed. However, possible structures do not appear equally frequently. The stable crystal structure of the elements at low temperature (and also at room temperature, whenever the two are di erent) and atmospheric pressure are listed in Appendix B. For several elements, further so-called allotropic modifications are possible. A quick glance at the table shows that about one-third of the elements are crystallized in one of four structures: cI2 and cF4 of the cubic system and hP2 and hP4 of the hexagonal system. (The nomenclature used above will be presented in the next section.) When the crystal structure of two-component compounds of composition AB is examined, the dominance of a small number of structure types is once again noticed. This is explained by the nature of the forces that hold crystals together; therefore we shall investigate the relation between crystal structure and bonding in the closing section of this chapter. Before that we shall study some frequent structures observed in elements and simple compounds – and also take a look at a handful of more complex but physically interesting structures.

7.1 Types of Crystal Structures

Two crystals are said to belong to the same structure type when their space groups and the coordinates of the atoms within the Bravais cell are identical. To be more precise, in addition to the space groups, the stoichiometric compositions have to be identical as well. However, when atoms are not in

204 7 The Structure of Crystals

Table 7.1. The Strukturbericht symbol, name, prototype, and Pearson symbol for a number of simple crystal structures and the Schoenflies and international notations for their space groups

Crystal structure

Proto-

Pearson

Symbols for

Symbol

Name

type

symbol

the space group

A1

face-centered cubic

Cu

cF4

Oh5

F m3m

A2

body-centered cubic

W

cI2

Oh9

Im3m

A3

hexagonal

Mg

hP2

D64h

P 63/mmc

close packed

A3

double hexagonal

La

hP4

D64h

P 63/mmc

close packed

A4

diamond

C

cF8

Oh7

F d3m

A8

γ-selenium

Se

hP3

D34

P 3121

A9

graphite

C

hP4

D64h

P 63/mmc

A15

Cr3Si

cP8

3

¯

Oh

P m3n

Ah

simple cubic

α-Po

cP1

Oh1

P m3m

B1

sodium chloride

NaCl

cF8

Oh5

F m3m

B2

cesium chloride

CsCl

cP2

Oh1

P m3m

B3

sphalerite

ZnS

cF8

2

¯

Td

F 43m

B4

wurtzite

ZnS

hP4

C64v

P 63mc

B81

NiAs

hP4

D64h

P 63/mmc

C1

fluorite

CaF2

cF12

Oh5

F m3m

C2

pyrite

FeS2

cP12

6

¯

Th

P a3

C3

cuprite

Cu2O

cP6

4

¯

Oh

P n3m

C4

rutile

TiO2

tP6

D414h

P 42/mnm

C14

Laves phase

MgZn2

hP12

D64h

P 63/mmc

C15

Laves phase

Cu2Mg

cF24

Oh7

F d3m

D02

skutterudite

As3Co

cI32

Th5

Im3

D03

BiF3

cF16

Oh5

F m3m

D09

ReO3

cP4

Oh1

P m3m

D2f

UB12

cF52

Oh5

F m3m

D81

Fe3Zn10

cI52

Oh9

Im3m

E21

perovskite

CaTiO3

cP5

Oh1

P m3m

H11

spinel

MgAl2O4

cF56

Oh7

F d3m

L10

AuCu

tP2

D41h

P 4/mmm

L12

Cu3Au

cP4

Oh1

P m3m

L21

Heusler phase

AlCu2Mn

cF16

Oh5

F m3m

L22

Sb2Tl7

cI54

Oh9

Im3m

L 3

Fe2N

hP3

D64h

P 63/mmc

7.2 Cubic Crystal Structures

205

high-symmetry positions, their coordinates may di er slightly – but the local symmetry around the atoms should be the same everywhere.

Some characteristics of the crystal structure – namely the Bravais-lattice type and the number of atoms in the Bravais cell – are contained in the Pearson symbol. The generic code is xY n; x is the symbol of the crystal system, given in Tables 5.7 and 5.8 (a for triclinic, m for monoclinic, o for orthorhombic, t for tetragonal, h for trigonal and hexagonal, c for cubic); Y refers to the type of the Bravais lattice (P for primitive, C for base-centered, I for body-centered, F for face-centered, R for rhombohedral); and n gives the number of atoms in the Bravais cell.

However, the Pearson symbol does not specify how the atoms are arranged within the cell. Although in many cases symmetry requirements impose restrictions on the positions of the second, third, fourth, etc. atoms (if they were placed arbitrarily, some symmetries would be broken), the Pearson symbol does not identify the structure unambiguously.

Various nomenclatures are used for specifying the structure type more precisely in the physical, chemical, and crystallographic literature. One of them is the Strukturbericht designation.1 Here letters A, B, C indicate whether it is a one-component crystal, or a two-component one with a composition XY, XY2, XmYn, etc. Structures within the same group are distinguished by numbers. It is also common practice to denote the structure type by the chemical symbol for a characteristic example, a prototype. Several thousand structure types exist; a handful of the simplest are selected in Table 7.1, with their usual symbols and names as well as Pearson symbols and space-group notations. The majority of the listed structures belong to the cubic system, and a smaller part to the hexagonal structure; these are the commonest for chemical elements and compounds alike. In the following sections we shall examine some of them in detail – bearing, nevertheless, in mind, that only a very narrow selection of the wealth of structures can be presented here.

7.2 Cubic Crystal Structures

Crystals that belong to the cubic crystal system come in three di erent Bravais-lattice types: simple, body-centered, and face-centered.

7.2.1 Simple Cubic Structures

While it is rare among the elements and not too frequent among compounds, either, our discussion starts with simple cubic crystals. This choice is justified by common practice: when some physical quantities of a crystalline material need to be determined theoretically, the lattice is most often assumed to be simple cubic.

1From the title of the supplement of a renowned German journal on crystallography, Zeitschrift für Kristallographie. Strukturbericht means Structure Report.

206 7 The Structure of Crystals

a3

a2

a1

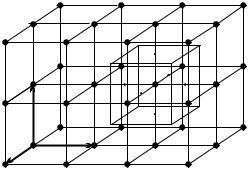
Fig. 7.1. Simple cubic lattice with the primitive vectors. The left cube (drawn with solid lines) is the primitive cell; the right one is the Wigner–Seitz cell around a lattice point

The primitive vectors of the simple cubic lattice are mutually perpendicular and of equal length. Figure 7.1 shows such a lattice with its primitive cell. Choosing a Cartesian coordinate system spanned by the unit vectors xˆ, yˆ, and zˆ along the axes of the cubic lattice, the primitive translation vectors are

a1 = axˆ , a2 = ayˆ , a3 = azˆ ,

(7.2.1)

where the edge length a of the primitive cell is the lattice constant. The volume of the primitive cell is thus v = a3. The Wigner–Seitz cell is also cubic, with the same dimensions.

To determine the reciprocal lattice of the simple cubic lattice, consider matrix Asc constructed from the above primitive vectors according to (5.2.3), and its inverse:

Asc = a	0 1 0	,	Bsc = 2a			0 1 0	.	(7.2.2)
	1 0 0			π		1 0 0
	0 0 1					0 0 1

Using the definition (5.2.10), the primitive vectors of the reciprocal lattice are

b1 =	2π	xˆ ,	b2 =	2π	yˆ ,	b3 =	2π	zˆ .	(7.2.3)
	a			a			a

These primitive vectors generate a simple cubic lattice with lattice constant 2π/a, thus the reciprocal lattice of a simple cubic lattice is another simple cubic lattice. Choosing the Brillouin zone as the domain of inequivalent k vectors instead of the primitive cell spanned by the bi, this is also found to be cubic, with the same edge length, 2π/a. The volume of the Brillouin zone is thus (2π)3/a3.

In the previous chapter it was shown that the eigenstates of a crystalline system may be specified in terms of the wave vectors k (as quantum numbers) defined in the Brillouin zone. We shall extensively use the convention of

7.2 Cubic Crystal Structures

207

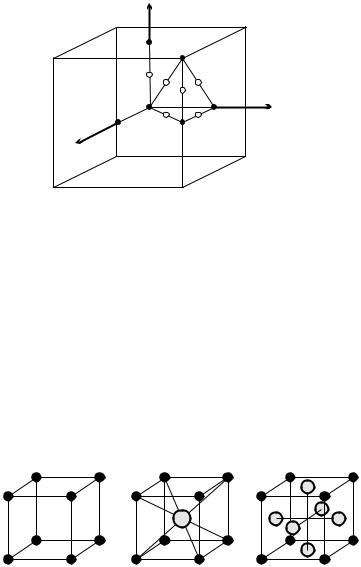
denoting special points of high symmetry by specific letters in the description of lattice vibrations and electronic states. The special points of the Brillouin zone of a simple cubic lattice and their letter symbols are shown in Fig. 7.2.

kz
	2 a
	X	R
		S	2 a
	T		ky
		Z
		M
kx

Fig. 7.2. The Brillouin zone of a simple cubic lattice with the special points and their letter symbols

¯

The point group of a simple cubic (cP) Bravais lattice is m3m (Oh). We have seen that, depending on the choice of the basis, a part of the symmetries may be broken. Below we shall mention some structures in which the introduction of a basis does not break any of the symmetries of the cube – that is,

¯ 1

whose space group is P m3m (Oh). This imposes severe restrictions on atomic positions. The structures will be specified by the number and position of the atoms in the basis.

The simplest crystal has one atom per unit cell; its Pearson symbol is cP1, and its Strukturbericht symbol is Ah. The unit cell contains one atom, and so lattice points can be chosen as atomic positions. This is shown in Fig. 7.3(a). Very few natural crystals have this structure: among the elements α-polonium is the only one.

(a)

(b)

(c)

Fig. 7.3. Primitive cell for simple cubic structures with one-, two-, and four-point bases. (a) Monatomic cP1 (Ah or Po) structure; (b) diatomic cP2 (B2 or CsCl) structure; (c) tetratomic cP4 (L12 or Cu3Au) structure

208 7 The Structure of Crystals

The reason for this is the bad space filling of this arrangement: each atom has only six nearest neighbors. The number of nearest neighbors, called the coordination number, is an important property of the crystal. In a monatomic simple cubic structure this number is thus 6. Even though atoms are in contact along the axes, large volumes are left empty among them in the interior of the cells. Space filling can be quantitatively characterized by the packing fraction (also called the atomic packing factor, APF), the ratio of the volume of the atoms considered as touching spheres to the volume of the cell. When a monatomic simple cubic lattice is constructed from spheres of radius r in contact with each other, the edge length is a = 2r. The volume occupied by the (single) atom is 4r3π/3 = πa3/6. This gives a packing fraction of π/6 = 0.524.

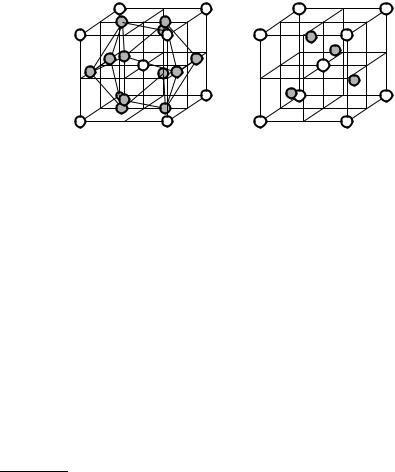
The lattice is more densely filled when the empty region among the atoms sitting at the vertices of the cubes is occupied by further atoms. When the basis is made up of two atoms, cubic symmetry is preserved only if one of them is in a vertex and the other is at the center of the primitive cell. In this arrangement – shown in Fig. 7.3(b) – the primitive cell contains two atoms, hence the Pearson symbol is cP2.

A typical example for simple cubic structures with such a basis is cesium chloride (CsCl), thus this arrangement is frequently called CsCl structure. The traditional crystallographic designation is B2 structure. Positively charged Cs+ ions (cations) sit in point 000 of each primitive cell, while negatively charged Cl− ions (anions) sit at the centers 12 12 12 . It is readily seen in the figure that each ion is surrounded by eight oppositely charged ions forming a cubic environment, the coordination number is therefore 8. Among twocomponent compounds of composition AB this structure ranks among the most frequently occurring ones. Among others, brass (CuZn, β-brass) belongs to this group.

A cubic lattice cannot be decorated with a three-point basis in such a way that cubic symmetry is preserved. However, when the basis contains four atoms, several possibilities exist. In one of them, shown in Fig. 7.3(c), atoms are found at the vertices and face centers, and the chemical composition is AB3. This structure is denoted by cP4 or (in traditional crystallographic notation) by L12. A typical example is the ordered phase of the alloy Cu3Au, which is why it is also called Cu3Au structure. The “A” atoms (in the above example, Au) sit at the vertices, while the “B” atoms (Cu) sit at the face centers. Thus the atomic coordinates in the basis are 000 for the Au atom and 0 12 12 , 12 0 12 , and 12 12 0 for the Cu atoms. Each atom has 12 nearest neighbors in this array, the coordination number is therefore 12. Au atoms are surrounded by Cu atoms exclusively, and cubic (Oh) symmetry is locally preserved. Among the nearest neighbors of Cu atoms there are four Au and eight Cu atoms; the local symmetry is only tetragonal (D4h).

Some further examples with more complicated bases are shown in Fig. 7.4;

¯ 1

symmetries of the space group P m3m (Oh) are preserved in each arrangement. The primitive cell contains four atoms in the ReO3 (or D09) structure, too,

7.2 Cubic Crystal Structures

209

thus its Pearson symbol is also cP4. Rhenium atoms sit at the vertices and oxygen atoms at the midpoints of the edges, i.e., at 12 00, 0 12 0, 00 21 .

(a)

(b)

(c)

Fig. 7.4. Simple cubic structures with four, five, and seven atoms per primitive cell. (a) cP4 (D09); (b) cP5 (E21 or perovskite); (c) cP7 (D21) structure

The cubic perovskite structure2 contains five atoms per primitive cell. Its traditional symbol is E21 and its Pearson symbol is cP5. In its prototype, CaTiO3, the large cations (Ca2+) sit at the vertices of the cube, the small cations (Ti4+) at the cell center, and the large anions (O2−) at the face centers 0 12 12 , 12 0 21 , 12 12 0. The large cation is thus surrounded by 12 anions, while the small cation by just 6.

The basis is composed of seven atoms in the CaB6 structure (D21, cP7). Here Ca ions sit at the vertices of the cube, and the six boron ions inside the primitive cell are along the lines between the body center and the face centers. The distance from the body center is such that each boron atom is surrounded by five others at equal distances – at points that are not of

	particularly high symmetry otherwise. The coordinates of the boron ions are
		1		1 1		1		1		1		1 1		1		√
	(		± x)		;		(		± x)		, and		(		± x), where x = 1 −		2/2 = 0.293. Their
		2		2 2		2		2		2		2 2		2

coordination number is 5 – while that of Ca ions is much higher, 24.

Other choices for the basis may also preserve the full symmetry of the space

¯

group P m3m. For example, when the composition of the compound/alloy is AB, with one type of atom at the face centers of the cell and the other at the edge centers. This structure (denoted by the Pearson symbol cP6) is observed in NbO. Symmetries remain the same when a third kind of atom, C is placed at the vertices (A3B3C). Much more complicated is the BaHg11 (D2e, cP36) structure. Here barium atoms sit at the edge centers, one mercury atom is located at the center of the cell, and the others – 32 further mercury atoms per primitive cell – around the vertices and edge centers in an array that preserves symmetry.

Naturally, in many more cases the symmetry of the crystal is reduced because of the lower symmetry of the basis. We shall briefly mention just two of them, the A15 and C3 structures. The first one is of particular importance as materials with this structure held the record for the superconducting transition temperature for many years, and this was essentially due to some

2After the mineralogical name of CaTiO3 – although the actual structure of this mineral is distorted in its ground state: its space group is only P nma.

210 7 The Structure of Crystals

characteristics of the structure. The primitive cell of the A153 (Cr3Si) structure contains the atoms of two molecules; its Pearson symbol is therefore cP8. As it is illustrated in Fig. 7.5, silicon atoms are located at the vertices and

body centers of the cells, while chromium atoms are found at points of lower

symmetry, 12 0 41 and 12 0 43 – as well as 0 14 12 , 0 43 12 , 14 12 0, and 34 12 0, which are obtained from the former two by rotations around the space diagonal. Each

Si atom is thus surrounded by 12 Cr atoms in an icosahedral arrangement. Fourfold rotations around the x-, y-, and z-axes are no longer symmetries, unless they are followed by a translation along the face diagonal perpendicular

to the axis of rotation. Rotation axes are thus replaced by screw axes. The

¯ 3 space group of A15 compounds is therefore P m3n (Oh).

(a)

(b)

Fig. 7.5. Atomic arrangement in the primitive cell of compounds (a) of composition AB3 and structure A15; (b) of composition A2B and structure C3

The prototype of the C3 structure is cuprite, Cu2O. The primitive cell contains two molecules, whereby its Pearson symbol is cP6. More generally, the composition of the material is A2B; atoms of type B are now located at the vertices and body centers of each primitive cell, while atoms of type A are found at 14 14 14 , 34 34 14 , 34 14 34 , and 14 34 34 . Once again, fourfold rotations are no longer symmetries unless combined with a translation along the space diagonal. Moreover, the same applies to inversion in this case. The space group

¯

4

is therefore P n3m (Oh).

7.2.2 Body-Centered Cubic Structures

In the structures presented in the previous subsection either the atoms located at the vertices were di erent from those at the bodyor face-centers of the cubic cell, or the atoms were of the same species but the basis was such that the surroundings of the atoms at the vertices and at the centers were di erent. In either case, the edge vectors of the cube were the primitive vectors. A di erent

3Recall that in the Strukturbericht designation the letter A is reserved for structures that occur in chemical elements. An elemental example for the A15 structure is the metastable β phase of tungsten (W).

7.2 Cubic Crystal Structures

211

situation arises when the atoms or groups of atoms sitting at the vertices and at the centers of the cubic cells are the same and so are their surroundings. Then the cubic unit cell is not a primitive cell any more, as the crystal is taken into itself by a translation through half the space diagonal of the cell. The Bravais lattice is thus extended to include body centers in addition to vertices of the cube. The new lattice is called body-centered cubic (bcc).

The body-centered cubic lattice can be conceived to be built up of two interpenetrating simple cubic lattices that are displaced by half the space diagonal of the cubic cell with respect to one another. It is then customary to speak of two sublattices. It should be emphasized that if the two sublattices become inequivalent – for example, when the two components of a disordered alloy start to become ordered on separate sublattices in a disorder–order transition

– then the initial structure, a body-centered cubic lattice with a monatomic basis is transformed into a simple cubic lattice with a diatomic basis.

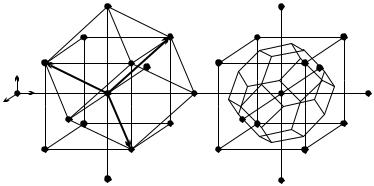
Primitive vectors of the bcc lattice are usually chosen to join the center of the cube with three vertices, as illustrated in Fig. 7.6(a). Denoting the edge length of the cube by a,

a1 =

a

(−xˆ + yˆ + zˆ) ,

a2 =

a

(xˆ − yˆ + zˆ) ,

a3 =

a

(xˆ + yˆ − zˆ) .

(7.2.4)

2

2

2

	a1
z	a2
x	y
(a)	a3
	(b)

Fig. 7.6. Body-centered cubic crystals: (a) the primitive cell with the primitive vectors; (b) the Wigner–Seitz cell

The figure clearly shows that the primitive cell of volume a3/2 – spanned by the primitive translation vectors – is rhombohedral, therefore it does not possess the symmetries of a cube. For this reason, the cubic Bravais cell (conventional unit cell) is preferred. Its edge vectors are given by

a = a2 + a3 = axˆ , b = a1 + a3 = ayˆ , c = a1 + a2 = azˆ . (7.2.5)

Instead of the primitive cell Fig. 7.6(a) the Wigner–Seitz cell is sometimes used; their volumes are equal but the latter is more symmetric. To

212 7 The Structure of Crystals

construct the Wigner–Seitz cell consider the body center of a Bravais cell. It has eight nearest neighbor lattice sites in space-diagonal directions and six second neighbor sites, located at the centers of adjacent cubes. The object bounded by the perpendicular bisector planes of the segments between the body center and these neighbors is an Archimedean solid, a truncated regular octahedron. In the directions of the eight nearest neighbors its faces are regular hexagons, while in the directions of the six second neighbors they are squares. The Wigner–Seitz cell, shown in Fig. 7.6(b), possesses every symmetry of the cube.

To specify the reciprocal lattice, first the matrix A is expressed in terms of the reciprocal vectors – see (5.2.3) –, and then its inverse is taken:

Abcc = 2

−1

1

1

,

Bbcc =

a

1 0 1

.

(7.2.6)

a

1

1

1

2π

0 1 1

−1 −1

1

1 1 0

Using (5.2.10), the primitive vectors of the reciprocal lattice are

b1

=

2π

(yˆ + zˆ) ,

b2

=

2π

(zˆ + xˆ) ,

b3 =

2π

(xˆ + yˆ) .

(7.2.7)

a

a

a

The reciprocal lattice generated by these vectors is a face-centered cubic lattice of edge 4π/a, as shown in Fig. 7.7. The Brillouin zone – obtained via Dirichlet’s construction – is drawn with dashed lines in the left part; special points of the Brillouin zone and their letter symbols are marked in the right part.

			kz		4 a		kz
								H
		4 a
					b1	4 a			P
		b2
									D
				b3
k						ky			ky
	x						G	N
							kx

Fig. 7.7. The reciprocal lattice of a body-centered cubic lattice and its Brillouin zone with special points

The Pearson symbol for a body-centered cubic structure, with a single atom per lattice point in the Bravais lattice is cI2, as each Bravais cell contains