Fundamentals of the Physics of Solids / 05-Symmetries of Crystals

5.4 Rotation and Reflection Symmetries in Crystals

149

c	a1

a2

b

a a3

c

a1	a	2

b

a3

a

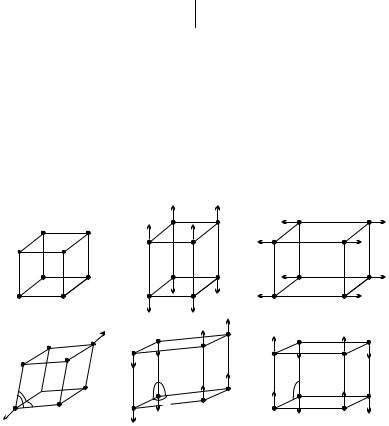
Fig. 5.22. Primitive translation vectors and Bravais cells for body-centered and face-centered cubic lattices

In addition to the vertices, the cubic Bravais cells or conventional unit cells now contain lattice sites either at the body centers or the face centers. These lattices are considered to belong to di erent lattice types because they cannot be continuously deformed into one another or into a simple cubic lattice without breaking some symmetries. For example, if the length of the primitive vectors were left unaltered but the relative angles were changed, only symmetries typical of the trigonal system could be conserved upon the smallest deformation. The lattice type that contains a site at the center of the Bravais cell is called body-centered ; its symbol is I. The lattice type that contains a site at each face center is called face-centered ; its symbol is F .

From the above examples one may expect that new lattice types of the same crystal system can be obtained by adding further sites at special positions of the primitive cell – at the body center, at the centers of a pair of opposite faces, or at the center of each face provided the point-group symmetry is unchanged. More general locations are certainly excluded since all the sites of the original lattice have to be reached by integer linear combinations of the new, shorter primitive translation vectors.

The seven crystal systems and the three types of centering could thus be expected to give rise to 21 types of centered lattices. In reality, only seven centered lattice types appear as centering does not always lead to new lattice types: in particular, in the triclinic system centering does not lead to a single new type. In other cases symmetries of the simple lattice are broken in the centered lattice. The new lattice types and the primitive ones are listed Table 5.8 for each crystal system.

The variety of notational conventions used for point groups exists for Bravais lattice types, too. In the Schoenflies notation the subscript of Γ specifies the crystal system (t = triclinic, m = monoclinic, o = orthorhombic, q = tetragonal, rh = rhombohedral, h = hexagonal, c = cubic), and the superscript refers to the centering the Bravais cell (c = base-centered, v = bodycentered, f = face-centered). Another convention uses a code of the form xY ,

150 5 Symmetries of Crystals

Table 5.8. The seven crystal systems and the fourteen types of Bravais lattices

Crystal system		Point group				Type
Name	Symbol			P	C	I	F R
Triclinic	a	¯	Ci	Γt
		1			Γmc
Monoclinic	m	2/m C2h		Γm
Orthorhombic	o	mmm	D2h	Γo	Γoc	Γov	Γof
Tetragonal	t	4/mmm D4h		Γq		Γqv
Rhombohedral	h	¯	D3d				Γrh
		3m
Hexagonal	h	6/mmm D6h		Γh		v	f
Cubic	c	¯	Oh	Γc
		m3m				Γc	Γc

where x is the international symbol for the crystal system (2nd column), and Y – one of the letters P , C (S), I, or F – specifies the centering type of the lattice. The rhombohedral (trigonal) lattice is an exception: although it is a primitive lattice, its centering type is denoted by R. Thus hP stands for hexagonal, and hR for rhombohedral crystal system. The reader will understand in hindsight why the rhombohedral system appears as a nonprimitive type of the hexagonal system. A third notation uses a code of the form Y x, where Y , once again, refers to the centering type (Y = P , C, I, F , R), and x is the short international symbol for the point group of the Bravais lat-

v	¯
tice. E.g., for body-centered cubic lattices the notations Γc	, cI, and Im3m

are used equally. All three notations are given in parentheses at the listing of Bravais-lattice types.

Below we list the fourteen Bravais-lattice types, together with the relations among the vectors spanning the primitive cell and the Bravais cell. (Bravais cells are shown in Fig. 5.23.) The two triplets of vectors are the same for primitive lattices but not for nonprimitive ones. As mentioned at the introduction of primitive translation vectors on page 111, there is some arbitrariness in their choice. That is why the choice of vectors presented below is not the only one used in the literature.

¯

1. Triclinic (aP , P 1, Γt). The three basis vectors (a = a1, b = a2, c = a3) can point to any directions, and their lengths are arbitrary, too: a = b = c,

α = β = γ.

2. Simple monoclinic (primitive monoclinic) (mP , P 2/m, Γm). The lengths of the three basis vectors are arbitrary, a = b = c, however one of them (customarily chosen as b) is perpendicular to the plane spanned by the others, α = γ = 90◦ = β. In rectangular coordinates the primitive vectors are given by a = a1 = (a sin β, 0, a cos β), b = a2 = (0, b, 0), c = a3 = (0, 0, c).

3.Centered monoclinic (base-centered monoclinic) (mC or mS, C2/m, Γmb ). A lattice site is added at the center of either rectangular face (base) of the simple monoclinic Bravais lattice. When the vectors specified in the

5.4 Rotation and Reflection Symmetries in Crystals

151

	c			c
		b		b
a			a

aP (P1¯)

mP (P2/m)

c

b

a

oP (Pmmm)

c

a

oC (Cmmm) oI (Immm)

a
	a
a	a

c
	b
a
mC (C2/m)

oF (Fmmm)

c

120°	a
a

tP (P4/mmm)

tI (I4/mmm)

hR (R3¯m)

hP (P6/mmm)

a

a

cP (Pm3¯m)

a

cI (Im3¯m)

cF (Fm3¯m)

Fig. 5.23. The fourteen types of three-dimensional Bravais lattices

simple monoclinic case are chosen as the edge vectors of the Bravais cell of sides a, b, c, i.e., a = (a sin β, 0, a cos β), b = (0, b, 0), c = (0, 0, c), then the primitive translation vectors may be chosen as a1 = a, a2 = 12 (a + b), a3 = c. The three primitive vectors are of unequal length, and neither two are perpendicular. Nevertheless the lattice is not triclinic, as the orientation of the vectors is such that 2a2 − a1 is perpendicular to the plane spanned by a1 and a3. This property gives rise to a twofold symmetry axis along the direction b = 2a2 − a1.

152 5 Symmetries of Crystals

Note that the base-centered monoclinic Bravais lattice can also be considered as a body-centered monoclinic Bravais lattice, as it is sometimes done in the literature. When 2a2 − a1 is perpendicular to the plane spanned by a1 and a3 then the choice a = a1 − a3, b = 2a2 − a1, c = a3 leads to a monoclinic Bravais cell that has a lattice site at its body center.

4.Simple orthorhombic (primitive orthorhombic) (oP , P mmm, Γo). The lengths of the three basis vectors are arbitrary, a = b = c, however they are mutually perpendicular: a1 = a a2 = b a3 = c a1. In

rectangular coordinates, a1 = (a, 0, 0), a2 = (0, b, 0), a3 = (0, 0, c). The Bravais cell is the same as the primitive cell. a = b = c, α = β = γ = 90◦.

5.Single-face-centered orthorhombic (base-centered orthorhombic) (oC or oS, Cmmm, Γob). The Bravais cell has the characteristic properties of a simple orthorhombic Bravais lattice. Its sides and angles satisfy the relations a = b = c, α = β = γ = 90◦. However, an additional lattice site is found at the centers of two equivalent opposite faces of the Bravais cell.

This	implies that the primitive translation vectors are a			1	=	1	(a,	−	b, 0)
	1					2			,
a2 =	2	(a, b, 0), and a3	= (0, 0, c). Vectors a1 and a2 are not perpendicular

to one another but a3 is perpendicular to them – therefore the three vectors seemingly form a monoclinic system. If, however, a1 + a2 and a2 − a1 are also perpendicular then additional symmetries appear, resulting in

a symmetry group mmm (D2h) instead of 2/m (C2h).

6.Body-centered orthorhombic (oI, Immm, Γov). The sides and angles of the Bravais cell once again satisfy the relations a = b = c, α = β = γ = 90◦,

however the additional lattice site is now found at the center of the cell. A

customary choice for the primitive translation vectors is a1 = 12 (−a, b, c), 1 (a, −b, c), a3 = 12 (a, b, −c). These are related to the edge vectors

of the Bravais cell through a = a2 + a3, b = a1 + a3, c = a1 + a2. Note that it is equally possible to choose two primitive vectors along the sides of the Bravais cell, a1 = a = (a, 0, 0), a2 = b = (0, b, 0); in this case the third has to satisfy c = 2a3 − (a1 + a2) – that is, a3 = 12 (a, b, c).

	7. All-faces-centered		orthorhombic				(face-centered orthorhombic) (oF ,
	F mmm, Γ f). The		Bravais	cell is			the same as in		other orthorhombic
	o	a = b = c				α = β = γ = 90◦		,	however additional
	Bravais lattices,				,

lattice sites are now found at each face center. The customary choice

for the	primitive translation vectors is a1 =	1	(0, b, c), a2 =	1	(a, 0, c),
		2		2
a3 = 21	(a, b, 0). These are related to the edge vectors of the Bravais cell

through a = −a1 +a2 +a3, b = a1 −a2 +a3, c = a1 +a2 −a3. If a primitive vector is chosen to lie along the edge of the Bravais cell, a1 = a = (a, 0, 0), then the two others have to be chosen in such a manner that b = 2a2 −a1

and c = 2a3 − a1 are perpendicular to a1. This implies a2 = 12 (a, b, 0), a3 = 12 (a, 0, c).

8.Simple tetragonal (primitive tetragonal) (tP , P 4/mmm, Γq). The three primitive vectors are mutually perpendicular, but only two of them are

of equal length: a1 a2 a3 a1, |a1| = |a2| = |a3|. The Bravais cell is the same as the primitive cell. a = a1 = (a, 0, 0), b = a2 = (0, a, 0), c = a3 = (0, 0, c), a = b = c, α = β = γ = 90◦.

5.4 Rotation and Reflection Symmetries in Crystals

153

9.Body-centered tetragonal (tI, I4/mmm, Γqv). To obtain a new type of Bravais lattice from the simple tetragonal lattice, one has to add a lattice

site at the body center of each Bravais cell. The relations a = b = c, α = β = γ = 90◦ continue to hold for the Bravais cell, however the

primitive vectors can now be chosen as a1 = 12 (−a, a, c), a2 = 12 (a, −a, c), a3 = 12 (a, a, −c). Similarly to the case of the body-centered orthorhombic lattice, the primitive vectors are related to the edge vectors of the Bravais

cell by a = a2 + a3, b = a1 + a3, c = a1 + a2. Once again, it is possible to choose two primitive translation vectors along the sides of the Bravais cell, e.g., a1 = a = (a, 0, 0), a2 = b = (0, a, 0); in this case the third vector

has to satisfy the condition c = 2a3 − (a1 + a2) – that is, a3 = 21 (a, a, c).
				¯
10. Rhombohedral (hR, R3m, Γrh). The three primitive vectors are of equal
length and make equal (but not right) angles with each other. As the
three vectors cannot be coplanar, their angles can be chosen to be smaller
than 120◦ without any loss of generality. The choice a = a1, b = a2,
c = a	implies			a = b = c	and	120◦ > α = β = γ = 90◦				. In rectangular
3
coordinates a customary choice for the primitive vectors is a1 = (a, 0, c)
1	√				1		√
a2 = 2	(−a, 3a, 2c), a3 =				2 (−a,		− 3a, 2c).

11.Simple hexagonal (primitive hexagonal) (hP , P 6/mmm, Γh). Two of the

primitive vectors (a1 and a2) are of equal length and make an angle of 120◦; the third one (a3) is perpendicular to them. The Bravais cell is the

same as the primitive cell. A possible choice for the primitive vectors is
1	√
a = a1 = 2	( 3a, −a, 0), b = a2 = (0, a, 0), c = a3 = (0, 0, c). a = b = c,
α = β = 90◦, γ = 120◦.

The rhombohedral Bravais lattice may also be considered as a centered version of the hexagonal lattice. This is reflected by the notation hR. Two lattice sites need to be added to the Bravais cell of a hexagonal lattice, at

2 a +	1 b +			1 c and			1 a + 2 b + 2 c. In rectangular coordinates these points
3	3			3			3	3			3
						1	√				1						1	√			1	2
are expressed as								3a, 0,				and											. The primitive vectors
						3					3 c						6		3a, 2 a,			3 c
in this new				lattice are thus
	1	√			1							1	√					1			1			1 √		1	1
a1 =											−			3a,									= −
	3	3a, 0,			3 c , a2 =							6						2 a,			3 c , a3			6	3a, −2 a,		3 c .
These vectors are oriented										the same way as the primitive vectors of a sim-

ple rhombohedral lattice. However, because of centering, this new lattice has a lower symmetry than the hexagonal one, which justifies considering

it as a di erent lattice type.				¯
12. Simple cubic (primitive cubic) (cP ,
				P m3m, Γc). The three primitive vec-
tors are of equal length and mutually perpendicular: a1 a2 a3 a1
and |a1| = |a2| = |a3|. Here, too, the Bravais cell is the same as the
primitive cell. a = b = c, α = β = γ = 90◦.
			¯	v
13. Body-centered cubic (bcc) (cI, Im3m, Γc ). As above, the Bravais cell is
cubic,		i.e., its	parameters satisfy the conditions a = b = c, α = β =
γ = 90◦, however an additional lattice point is found at the center of
the	cell. Thus the primitive vectors may be chosen as a					= 1	(	a, a, a)
		1	1		1	2	−	,
a2 =		2 (a, −a, a), a3 = 2 (a, a, −a). Just like in body-centered tetragonal

154

5 Symmetries of Crystals

lattices, they are related to the edge vectors of the Bravais cell by a =

a2 + a3, b = a1 + a3, c = a1 + a2. As an alternative, two primitive vectors

can again be chosen along the sides of the Bravais cell, a1 = a = (a, 0, 0),

a2 = b = (0, a, 0), in which case the third must satisfy the requirement

c = 2a

3 − (a1 + a2)

– that is,

1

a, a)

a3 =¯2

(a, f .

lattice pa-

14. Face-centered cubic

(fcc) (cF , F m3m, Γc ). Once again, the

rameters of the Bravais cell

satisfy

the conditions a = b

= c and

α = β = γ = 90◦, however additional lattice sites are found at each

face center. As it has been mentioned, the customary choice for the prim-

itive vectors is a1 = 21 (0, a, a), a2 = 21 (a, 0, a), a3 = 21 (a, a, 0). These are

related to the edge vectors of the Bravais cell by a = −a1 + a2 + a3,

b = a

a + a , c = a

+ a2

−

a3. Another common choice is taking two

1

− 2

3

1

1

1

perpendicular vectors, a1 =

2

(a, −a, 0) and a2 = 2 (a, a, 0), and choosing

the third one so that

2a

−

(a + a )

should be

perpendicular to the plane

3

1

2

1

of a1 and a2. This requirement is satisfied by

a3 = 2 (a, 0, a). The three

edge vectors of the Bravais cell are mutually perpendicular and of equal length: a = a1 + a2, b = a2 − a1, and c = 2a3 − (a1 + a2).

5.4.6 The Hierarchy of Crystal Systems

The previous enumeration of crystal systems proceeded from the simplest point groups to those with more symmetry elements. By adopting the opposite approach, a certain natural hierarchy can be observed among crystal systems. The most straightforward way to demonstrate this is to take a cubic (in two dimensions: square) or hexagonal crystal system, and to reduce the symmetry by appropriate deformations of the crystal.

Of all two-dimensional point lattices square and hexagonal ones possess the highest symmetries. Small deformations cannot take them into one another. A small deformation of the square lattice – stretching one of its sides – leads to a simple rectangular lattice, while stretching a square lattice along its diagonal leads to a centered rectangular lattice. The same lattice type is obtained when a hexagonal lattice is stretched or compressed along a mirror line or in a direction perpendicular to it. Square and hexagonal crystal systems are thus said to be higher in the hierarchy than the rectangular one. Further (shearing) deformation of both types of rectangular lattices leads to oblique lattices. The hierarchy of two-dimensional crystal systems is summarized in Fig. 5.24.

In the three-dimensional case we shall start o with the most regular primitive cell, the cubic one. It can be deformed by pulling or pushing on two opposite faces: angles are left intact while a side is stretched or compressed. The result is a rectangular prism with a square base – an object with tetragonal symmetry.

By stretching the object in another direction, a general rectangular parallelepiped with orthorhombic symmetry is obtained. A further shearing deformation along one of the planes changes the inclination of the edge initially

5.4 Rotation and Reflection Symmetries in Crystals

155

Square (4mm) Hexagonal (6mm)

Rectangular (2mm)

Oblique (2)

Fig. 5.24. Hierarchy of two-dimensional crystal systems

perpendicular to the shearing plane. The result is an object that possesses only monoclinic symmetry. Finally, another shearing in another plane leads to the most general triclinic parallelepiped. The objects obtained through the above sequence of deformations of a cube are shown in Fig. 5.25.

a

a

a

a

a

a

		c		a		c
						b
		a			a
		c				c
			b
	a				a	b

Fig. 5.25. Bodies of lower symmetry obtained through subsequent deformations of a cube. The direction of deformation forces are shown by the single arrows

Trigonal and hexagonal crystal systems are not yet included in the above scheme. By stretching the cubic lattice along a space diagonal, a rhombohedral lattice is obtained. Another small deformation leads to a lattice that possesses the symmetries of the monoclinic crystal system. Small deformations of a cubic (regular) lattice cannot lead to a hexagonal lattice. On the other hand, deformations of a hexagonal lattice may lead to a lattice showing orthorhombic symmetry – more precisely, to a base-centered orthorhombic Bravais lattice. Figure 5.26 gives a summary of this hierarchy of three-dimensional crystal systems.

156 5 Symmetries of Crystals
Cubic (Oh )					Hexagonal (D6h )
Rhombohedral (D3d ) Tetragonal (D4h )
	Orthorhombic (D2h )

Monoclinic (C2h )

Triclinic (S2)

Fig. 5.26. Hierarchy of three-dimensional crystal systems

Each time the primitive cell is deformed, a symmetry is broken. Therefore the symmetries of a crystal system ranked lower in the hierarchy form a subgroup of the symmetries of the system ranked higher. The same hierarchy could have been derived by starting with the cubic and hexagonal point groups (Oh and D6h), and choosing smaller and smaller subgroups. One must, however, exercise due care: although the symmetry group D3d of the rhombohedral lattice is a subgroup of D6h, the symmetry group of the hexagonal lattice, the former should not be considered to lie under the latter in the hierarchy as no small deformation of the hexagonal lattice can lead to a rhombohedral one.

In the above presentation of the hierarchy of crystal systems we started o with a simple cubic lattice and arrived at lower-symmetry lattices through subsequent deformations. Analogously, one can start with a bodyor facecentered cubic lattice and track down deformed lattices with lower symmetries. It is a straightforward matter to prove that whichever cubic Bravais lattice type is taken, a suitably chosen deformation will take it into one of the tetragonal lattice types. Further deformations will transform any tetragonal lattice type into one of the orthorhombic lattices. The four orthorhombic lattice types are, in turn, deformed into either of the monoclinic lattice types. Finally, a small deformation of either monoclinic lattice type results in a triclinic lattice. Similarly to the case of the simple cubic lattice, when a faceor body-centered cubic lattice is stretched along the body diagonal, a rhombohedral lattice is obtained. As the hexagonal system has no centered type one can state that the hierarchy among crystal systems does not change when the various types within each system are taken into account. This hierarchy is of particular importance when the crystal classes are assigned to the crystal systems in the next section.

5.5 Full Symmetry of Crystals

157

5.5 Full Symmetry of Crystals

Up to this point translation symmetries (elements of the group T3) have been treated separately from the rotation and reflection symmetries (elements of the group G30) of the Bravais lattice. Translations, rotations, and reflections all together make up the full symmetry group of a crystal’s Bravais lattice. When a rotation or reflection (denoted by α) and a translation (tn) both take the lattice into itself then so does the succession of the two operations. In the Seitz notation23 this composite symmetry operation is denoted by

{α|tn} .

(5.5.1)

The order of the two operations is important as translations and rotations cannot usually be interchanged. Rotation (reflection) always comes first, and translation second. Because of this noncommutativity, the full symmetry group is the semidirect product of T3 and G30: T3 G30. Analogously, for two-dimensional lattices the full symmetry group is T2 G20.

When the translational symmetry of a crystal is identified and the primitive translation vectors are determined, the full crystal – lattice plus basis

– has to be considered. However, when studying the rotation and reflection symmetries of Bravais lattices, empty lattices are considered – i.e., the basis is altogether ignored. When the basis is taken into account, some rotational symmetries may be broken: the crystal may not be invariant under each rotation that takes the underlying lattice into itself. Invariance is preserved only when finite but spherical atoms or precisely spherical molecules sit at the lattice points. Since this is generally not the case, depending on the shape of the group of atoms or molecules around each lattice point (i.e., the internal symmetry of the basis), certain rotation and reflection symmetries of the underlying lattice may be broken in the crystal. On the other hand, the crystal may have additional symmetries that do not exist in the Bravais lattice. That is why even after the separate discussion of translational and rotational symmetries new features appear when the full symmetry of the crystal is considered.

5.5.1 Screw Axes and Glide Planes

Once again, we shall first consider the two-dimensional case, in which patterns are repeated along two spatial directions. Such structures are shown in Fig. 5.27.

The absence of a mirror line is apparent at first sight: neither drawing is left-right symmetric. It is readily shown, however, that the pattern is brought into coincidence with itself when a reflection in the vertical midline is followed by a vertical translation. In addition to the well-known mirror line, a new

23 F. Seitz, 1936.

158 5 Symmetries of Crystals

Fig. 5.27. Plane figures with glide lines on Escher’s drawings

type of symmetry element appears in two-dimensional structures: the glide line, customarily denoted by g.

Glide reflection {m|v} is a composite symmetry operation in which a reflection m in a mirror line of the plane is followed by a translation v along the direction of the mirror line, where v is not an integer multiple of any primitive vector of the lattice. The succession of the two operations may be a symmetry transformation even though neither reflection m nor translation through v is a symmetry. Nevertheless, the length of the translation vector v cannot be arbitrary. As the resultant of two such operations is a pure translation, translation along the glide line must cover half the distance that characterizes periodicity along that direction.

In three-dimensional crystals two new symmetry operations may appear. The first one is glide reflection in space. This is a reflection in a plane followed by a translation parallel to the plane that is not an integral multiple of primitive translations.24 The plane of the reflection is called the glide plane. Its Schoenflies symbol is σg and its international symbol is a, b, c, n, or d – depending on whether translation is along an edge, a face or body diagonal of the unit cell, through one-half or one-quarter of its length. Figure 5.28 shows a periodic structure with a glide plane.

In the other new symmetry operation α in {α|v} is a rotation. A crystal structure is said to possess an n-fold screw axis if it is brought into coincidence with itself by an n-fold screw rotation (also called a screw operation) – i.e., rotation through 2π/n around some axis followed by a translation along the

24A reflection followed by a translation perpendicular to the mirror plane is not a new symmetry operation: it is equivalent to a reflection in a parallel plane. Nevertheless glide reflections are often chosen in such a way that v has both parallel and perpendicular components.