Fundamentals of the Physics of Solids / 05-Symmetries of Crystals

5.5 Full Symmetry of Crystals

159

g

c/2 c/2

Fig. 5.28. Periodic structure with a glide plane

axis.25 The symmetry element is denoted by Cns in the Schoenflies notation and by nj in the international notation, where j runs over the values 1, 2, . . . , n−1, and refers to the succeeding translation – which is not arbitrary. The group property of symmetry operations implies that when the screw axis is twofold then rotation through 180◦ has to be followed by a translation along the axis through half the repeat distance (periodicity) in that direction. The symbol for this operation is 21. For a threefold screw axis translation has to be through either one-third or two-thirds of the repeat distance. The symbols for these operations are 31 and 32. In general, when the screw axis is n-fold, rotation through 2π/n is followed by a translation through j/n times the periodicity of the crystal. This is denoted by nj . Figure 5.29 shows objects with a fourfold screw axis.

c/4

c/4

c/4

c/4 0º

90º

Fig. 5.29. Periodic structures with a fourfold screw axis. Rotation is clockwise in one case and counterclockwise in the other; both are followed by a translation of the crystal through one-quarter of the lattice constant

25A rotation followed by a translation perpendicular to the rotation axis is not a new symmetry operation, either: it is equivalent to a rotation around a parallel axis. Nevertheless screw operations are often chosen in such a way that v has both parallel and perpendicular components.

160 5 Symmetries of Crystals

5.5.2 Point Groups of Crystals and Crystal Classes

Let us examine now how symmetries of the Bravais lattice are broken in the crystal when the basis has a lower symmetry than the Bravais lattice. As an example, we shall consider crystals whose underlying Bravais lattice is a simple cubic lattice and atoms at the lattice sites are surrounded by di erent atoms. Three di erent cases are shown in Fig. 5.30.

(a)

(b)

(c)

Fig. 5.30. Symmetry is either preserved or broken when a simple cubic Bravais cell is decorated with bases of various symmetries. (a) Symmetry of the point group Oh is preserved. (b) Symmetry is broken to Td. (c) Symmetry is broken to D4h

In the first case, among the atoms at the lattice points, atoms of another species (“black atoms”) are placed in each of the eight equivalent points

±ξ, ±ξ, ±ξ of the space diagonals. Then the atom at the lattice points is surrounded by 8 black atoms in a cubic arrangement – therefore the basis and the crystal itself possess cubic symmetry (Oh). The same situation arises when 6 neighboring atoms are arranged along the edges, forming an octahedron.

However, when the atom at the lattice point is surrounded by only four black atoms then the symmetry of the basis can no longer be cubic – and so the cubic symmetry of the lattice cannot be entirely preserved. When the four atoms are arranged on the space diagonals in the manner shown in Fig. 5.30(b)

– i.e., when the atom at the lattice point is surrounded by four black atoms arranged tetrahedrally – then only those rotational symmetries are preserved that take the tetrahedron into itself – namely, elements of the point group Td. The atom at the lattice point is surrounded by four black atoms in part (c), too, however the black atoms are now placed on the diagonals of one face (the base). Threefold rotational symmetry around the space diagonal is thus broken – however, fourfold rotational symmetry around one of the edges reappears. The point group of the five-point basis is D4h, which is also the point group of the rotational symmetries of the crystal.

These examples show that the crystal itself is not always invariant under each rotation and reflection of the point group of its Bravais lattice. Some symmetries may be broken because of the presence of a basis. The remaining operations form a group, which is necessarily a subgroup of the point group of

5.5 Full Symmetry of Crystals

161

the Bravais lattice. Therefore this group has to be one of the crystallographic point groups listed in Table 5.5, as the subgroups of the seven Bravais groups are precisely the 32 point groups given there.

The same group may appear as the subgroup of more than one Bravais group. In such cases the group is considered to belong to the crystal system that is lowest in the hierarchy. This classification is based on the empirical finding that when a lattice is decorated with a basis whose symmetry is lower than that of the Bravais lattice, the lattice itself will be deformed, and the relations among the lattice parameters will correspond to the lower-ranked crystal system. For example, when the lattice points of a cubic crystal are decorated with molecules of tetragonal symmetry (as above), and thus the cubic symmetry is locally broken, the lattice itself will undergo a tetragonal deformation. More generally: if the equality of two quantities (in our case: lattice constants) is not required by symmetry then – apart from few exceptional, accidental cases – these quantities will be di erent.

Note that two-dimensional crystallographic point groups may also be classified into crystal systems based on their hierarchy. When a point group may appear as the subgroup of several Bravais groups then it is classified under the lowest one in the hierarchy. Thus point groups 6mm, 3m, 6, and 3 belong to the hexagonal system, 4mm and 4 to the square system, 2mm and m to the rectangular system, and 2 and 1 to the oblique system.

The knowledge of the rotation and reflection symmetries of a crystal is important because internal physical processes should take place in the same way in all directions that are equivalent due to symmetry – and so crystal symmetries manifest themselves in macroscopic properties, too. For example, the elasticity or conductivity tensor has to be invariant under the transformations that take the crystal into itself. We shall make extensive use of the severe restrictions imposed by this property on the tensor elements.

The symmetry operations which transform into each other those directions of the crystal that are equivalent in terms of macroscopic properties form the point group of the crystal. The elements of this group can be obtained by replacing screw rotations by simple rotations and glide reflections by mirror reflections. To see this it has to be born in mind that macroscopic properties depend only on the relative arrangement of the atoms along some direction. Thus two directions are equivalent even when they are transformed into one another by a screw rotation or glide reflection instead of a pure rotation or reflection.

Obviously, each element of the point group of the crystal must be an element of the point group (Bravais group) of the crystal’s Bravais lattice. Hence the point group of the crystal must be a subgroup of the point group of the lattice. Thus the total number of such groups is the same as the number of subgroups of the Bravais groups of the seven crystal systems. Thirty-two subgroups are found – they correspond to the 32 crystallographic point groups

– thus a crystal’s point group is one of the crystallographic point groups, and the same notation is used for them.

162 5 Symmetries of Crystals

Crystals with the same point group are said to belong to the same crystal class. The 32 crystal classes received their names from finite objects whose symmetry group is the respective point group. For example, the crystal class with symmetry Oh is called the hexakisoctahedral class.

5.5.3 Space Groups

Besides translations, rotations, and reflections, the full set of symmetries of a crystal contains screw operations and glide reflections as well. These operations form a group, provided group multiplication – as for the translation group and the point group – is understood as the succession of two operations. Simple geometrical considerations lead to

{α |tn}{α|tn} = {α α|α tn + tn} .

(5.5.2)

The inverse of a transformation is given by

{α|tn}−1 = {α−1| − α−1tn} .

(5.5.3)

The group that contains all symmetry operations of a crystal is called its space group. Two-dimensional space groups are also called plane groups or wallpaper groups.

Plane Groups

To find all possible “space” groups (plane groups, wallpaper groups) of twodimensional crystals, we shall construct planar patterns that are periodic in both directions. To this end, we shall start with a two-dimensional Bravais lattice and decorate it with bases of appropriate symmetry. The groups of such patterns are the G22 groups. Some of them can be written as the semidirect product of the group T2 of translations in the plane with a suitably chosen two-dimensional point group G20. Suitable choice means that the point group in question must be a subgroup of the Bravais group of the Bravais lattice. This is possible when glide reflection is not a symmetry element of the plane group. The two upper drawings in Fig. 5.6 show that when an oblique cell is decorated with a figure that does not have a twofold axis – in other words, when the point group of the basis is lower than that of the Bravais lattice – then the crystal itself does not have a twofold axis, either. The plane group of such patterns is p1. On the other hand, when the basis has higher symmetry than the oblique Bravais lattice then the crystal is also invariant under the symmetry operations of the lattice. The plane group of such crystals (with a twofold rotation axis and a simple oblique Bravais lattice) is denoted by p2.

Two lattice types are possible for rectangular lattices (whose point group is 2mm). Primitive and centered lattices can be equally decorated with a basis that has two perpendicular mirror lines. This leads to the space groups p2mm

5.5 Full Symmetry of Crystals

163

and c2mm (in short notation: pmm and cmm). However, the basis may have only one mirror line instead of two. In this case the plane groups are pm and cm. When a rectangular lattice is decorated with a basis that has no mirror lines then it is deformed spontaneously into an oblique lattice.

In square lattices, which are invariant under the rotations and reflections of the point group 4mm, the basis itself may be invariant under 4mm operations. In this case the plane group of the crystal is p4mm (in short notation: p4m). If the symmetry of the basis is lower, and only fourfold rotations are preserved then the plane group is p4. In principle, the symmetry of the basis could also be the subgroup m of the point group 4mm. However, in this case the symmetry that links the two primitive vectors would be broken, and the square lattice would be deformed into a rectangular one. The resulting plane group would be pm.

When a hexagonal lattice is decorated with a basis that is also invariant under the symmetries of the point group 6mm, then the plane group of the resulting crystal is p6mm (in short notation: p6m). If the symmetry of the basis is lower, the lattice remains hexagonal as long as the point group of the basis is a subgroup of 6mm: either 3m, 6, or 3. The respective plane groups are p3m, p6, and p3. Motifs of symmetry 3m can be oriented in two di erent ways relative to the axes of the lattice, and so two plane groups can be generated. The threefold rotation axes are common in both of them, however the three mirror lines are either along or perpendicular to the three equivalent crystallographic axes. These are denoted by p31m and p3m1.

Using translations, rotations, and reflections of the lattice, 13 two-dimen- sional space groups have been constructed above. They are called the symmorphic groups or symmorphic plane groups. There exist further, nonsymmorphic groups that contain glide reflections as well. When investigating the symmetries of a periodic motif one has to bear in mind that patterns of the symmorphic space group may also have glide lines although these do not pass through the group’s characteristic n-fold axis. This is not the case for nonsymmorphic groups.

If a primitive rectangular lattice is decorated with such a basis that only one mirror line of the Bravais lattice is preserved and the other is replaced by a glide line, then the plane group is p2mg (in short notation: pmg). It is equally possible that both mirror lines are replaced by glide lines, then the plane group is p2gg (pgg). A motif with such symmetry is shown in Fig. 5.31(a). When one mirror line is completely absent and the other is replaced by a glide line, the pattern possesses the symmetries of the point group pg. Motifs with such symmetry were shown in Fig. 5.27.

A square lattice can be decorated with a basis in such a way that the mirror lines along the edges and diagonals of the square – intersecting each other at points of fourfold rotational symmetry – are no longer symmetries, but glide lines appear along the diagonals and parallel to the edges, while the

164 5 Symmetries of Crystals

(a)

(b)

Fig. 5.31. Two drawings of Escher with symmetries of two di erent plane crystallographic groups. (a) The plane group is p2gg and the Bravais-lattice type is primitive rectangular for the figure with two glide lines. (b) The plane group is p4gm and the Bravais-lattice type is square for the figure with one set of glide lines

fourfold rotation axes are preserved.26 The plane group is then p4gm (p4g). A pattern with such symmetry is presented in Fig. 5.31(b). Four nonsymmorphic groups are thus obtained, raising the total number of two-dimensional space groups to 17. Figure 5.32 shows periodic patterns that exhibit symmetries of two-dimensional space groups.

Three-Dimensional Space Groups

The group of symmetries of three-dimensional patterns that are periodic in three directions is the space group G33. Once again, some of them may be written as the semidirect product of the group of translations T3 with a threedimensional point group G30. This is possible when neither glide reflections nor screw rotations are among the symmetry elements. The group of rotations and reflections that take such a crystal into itself is either the point group of the Bravais lattice or one of its subgroups that belong to the same crystal system. By taking due care of the relative orientation of the rotational axes of the basis and the axes of the 6/mmm (D6h) group in the hexagonal system, 73 di erent symmorphic space groups are constructed. Apart from the hexagonal system, the space groups are unambiguously specified by the Bravais-lattice type and the crystal class. This is reflected by their symbol in the international notation.

26Two perpendicular mirror lines are still present among the symmetry elements, however they go through the midpoints of adjacent perpendicular edges of the square, and their intersection points possess only twofold rotational symmetry.

5.5 Full Symmetry of Crystals

165

p1

p2

pm

pg

cm

p2mm

p2mg

p2gg

c2mm

p3

p3m1

p31m

p6		p6mm
p4	p4mm	p4gm

Fig. 5.32. Motifs showing the symmetries of plane groups

166 5 Symmetries of Crystals

E.g., when a simple cubic lattice is decorated with a basis whose point group

¯	¯	¯	¯
is m3m, 432, 43m, m3, or 23, the space group of the crystal is P m3m, P 432,
¯	¯

P 43m, P m3, or P 23, respectively. When the original lattice type is bodyor face-centered cubic, I or F appears in the symbol of the space group.

In addition to the 73 symmorphic space groups there exist 157 nonsymmorphic space groups, which contain screw operations and/or glide reflections. The total number of three-dimensional space groups is thus 230. This result was first worked out by the crystallographer J. S. Fedorov (1890) and independently of him by the mathematician A. M. Schoenflies (1891). We shall mercifully spare the reader a complete listing as it would lead too far afield. The 230 space groups and their symmetries are most extensively treated in Volume A of the series International Tables for Crystallography. As an exam-

	¯
ple, we shall present the space groups that belong to class m3m (Oh) of the
cubic crystal system.
¯	1

The symmorphic space group P m3m (in Schoenflies notation: Oh) is the

space group of crystals whose underlying Bravais lattice is simple cubic and

¯

for which all elements of the point group m3m (Oh) – presented in Tables 5.1 and 5.4 – are symmetries. A nonsymmorphic space group is obtained if all rotations listed in Table 5.1 are symmetries but reflections listed in Table 5.4 take the crystal into itself only when followed by a translation along the space diagonal through one-half of its length. The generator of these rotoreflections

is {I|	1 1 1	¯
	2 2 2	}. Compared to the space group P m3m, all rotations are pure ro-

tations, however all mirror planes are replaced by glide planes. Consequently,

¯

its symbol is P n3n. In the Schoenflies notation space groups generated from the same point group are distinguished by a single superscript, its symbol is therefore Oh2 .

Di erent space groups are obtained when the space diagonals remain threefold rotation axes while the three principal axes and the six face diagonals become fourand twofold screw axes, respectively, with translation along the space diagonal. This means that the first 12 elements of Table 5.1 remain pure rotations while the next 12 are replaced by screw operations. If inversion remains a symmetry then along with it half of the reflections are also preserved and the other half are replaced by glide reflections. The resulting space group

¯

3

is called P m3n (Oh). When, on the other hand, the symmetry under inver-

sion is broken unless it is followed by a translation along the space diagonal,

¯
ordinary mirror planes of the space group P m3n are replaced by glide planes
– and vice versa. Consequently, the space group is denoted by	¯	4
	P n3m	(Oh).

There is no other way to obtain a cubic space group when starting with a simple lattice.

5.5.4 Symmetries of Magnetic Crystals

In the foregoing we have analyzed spatial transformations that take a point (x, y, z) of a crystal into an equivalent point. These form the group of spatial transformations. When ferroelectric or magnetic materials are studied, the

5.5 Full Symmetry of Crystals

167

transformation of the electric and magnetic dipole moments need to be taken into account as well. As a simple example, A. V. Shubnikov (1951) studied the symmetries of a system in which there is a two-valued variable s = ±1 at each site (x, y, z).

Because of the new variable, a new operation (R) appears, which is called antisymmetry. This takes the point characterized by the variables (x, y, z, s) into (x, y, z, −s). Adding this operation to the customary symmetry operations leads to magnetic point groups and magnetic space groups or Shubnikov (space) groups. The two values (s = ±1) are often referred to as “black” and “white” – and then the group is called “black-and-white group”.

Magnetic point groups contain rotations, reflections, and the antisymmetry operation. In addition to the 32 ordinary point groups of crystals (that do not contain the antisymmetry operation), another 32 appear which contain the antisymmetry operator R as a symmetry element. This is possible only when the values of s are both present in each lattice point. In magnetic terms this means that upward and downward magnetic moments are equally probable at each individual lattice point, and thus the average vanishes. This corresponds to the paramagnetic phase. Using black and white, these are the so-called gray groups. There are 58 other magnetic point groups that do not contain R itself only its combination with a rotation. They are the true magnetic groups in the sense that they may appear as points groups of ordered magnetic structures.

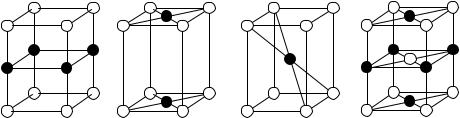
When translations are also taken into account, one may study magnetic (or black-and-white) lattices instead of ordinary Bravais-lattice types, in which all lattice points are equivalent. Besides displacements through translation vectors tn, operations of the form {R|v} are also allowed. Obviously, this may be a symmetry only when v is half a translation vector. In addition to the 14 ordinary Bravais-lattice types – in which lattice sites are of the same color –, 22 further Bravais-lattice types are found, which contain both black and white lattice sites. The new magnetic (or black-and white) lattice types with tetragonal and cubic structures are shown in Figs. 5.33 and 5.34.

Figure 5.33 shows that black-and-white Bravais lattices are built up of two interpenetrating Bravais lattices, a black and a white. In the case of a simple tetragonal lattice the relative displacement vector of the two sublattices is either one-half of the primitive vector along the fourfold axis, or the vector to

Fig. 5.33. Black-and-white Bravais lattices in the tetragonal crystal system

168 5 Symmetries of Crystals

Fig. 5.34. Black-and-white Bravais lattices in the cubic crystal system

the center of the base, or the vector to the center of the primitive cell. In a body-centered tetragonal lattice there is just one possibility: the relative displacement vector of the two sublattices must be in the direction of the fourfold axis, and its magnitude must be one-half of the height. This is equivalent to a translation of the second sublattice through half the face diagonal.

In a simple cubic Bravais lattice the two interpenetrating sublattices are displaced by half the space diagonal. Each black atom is surrounded by eight white atoms, and vice versa. In a face-centered cubic lattice the relative displacement is the half of either edge vector. In this case each black atom is surrounded by six white ones.

The combination of magnetic Bravais lattices and magnetic point groups gives rise to 1651 magnetic (or black-and-white) space groups. Just like for point groups, 230 of them are ordinary space groups that do not contain the antisymmetry operation at all. There are the same number of paramagnetic (or gray) space groups, in which the antisymmetry operation is a symmetry element in itself. In the remaining 1191 space groups antisymmetry appears only in combination with rotations, reflections, or translations.

The possible symmetries of real magnetic systems are even more complicated than that. Black-and-white groups may, at most, purport to give the symmetry groups of magnetic systems that can be described by the Ising model, in which the magnetic moment is represented by a two-valued variable. In the general case the magnetic moment vector points in di erent directions on di erent magnetic atoms, giving rise to noncollinear magnetic structures. Moreover, account must be taken of the fact that magnetic moments are also transformed by rotations. It should also be borne in mind that the magnetic moment m is an axial vector, which does not transform as a true vector under reflections. (This last property is easily understood when the magnetic moment is considered to be produced by a current loop. Upon reflection, the component perpendicular to the mirror plane does not change sign but the component in the plane does.) All this leads to a great wealth of possibilities for symmetries in magnetic systems that cannot be listed here. The issue of possible magnetic structures will be briefly discussed in Chapter 14 on magnetically ordered systems.