Практика ФКП

Министерство образования и науки Российской Федерации Уральский федеральный университет

имени первого Президента России Б.Н. Ельцина

Р. М. Минькова

Функции комплексного переменного в примерах и задачах

Рекомендовано методическим советом УрФУ в качестве учебного пособия для студентов,

обучающихся по программе бакалавриата и специалитета по направлениям подготовки 140800.62 – Ядерные физика и технологии;

141401.65 – Ядерные реакторы и материалы;

141405.65 – Технологии разделения изотопов и ядерное топливо;

140801.65 – Электроника и автоматика физических установок;

010900.62 – Прикладные математика и физика;

210100.62 – Электроника и наноэлектроника;

201000.62 –Биотехнические системы и технологии;

200100.62 –Приборостроение;

221700.62 – Стандартизация и метрология;

230100.62 – Информатика и вычислительная техника;

230400.62 –Информационные системы и технологии

Екатеринбург

УрФУ

2013

УДК 517(075.8) ББК 22.161я73 М62

Рецензенты:

кафедра прикладной математики Уральского государственного экономического университета (зав. кафедрой, доц., канд. физ.-мат. наук Ю.Б. Мельников);

старший научный сотрудник Института математики и механики УрО РАН,

проф., д-р физ.-мат. наук Е.Ф. Леликова;

Научный редактор − доц., канд. физ.-мат. наук Н.В. Чуксина

М62 Минькова, Р.М.

Функции комплексного переменного в примерах и задачах:

учебное пособие / Р.М. Минькова. Екатеринбург: УрФУ, 2013. 45 с.

ISBN

В данной работе разбирается решение типовых примеров и задач по следующим темам курса «Функции комплексного переменного»: функции комплексного переменного, их дифференцирование, интегрирование, разложение в ряды Тейлора и Лорана, вычеты и их применения, операционное исчисление.

Работа предназначена для студентов физико-технического факультета.

Библиогр.: 10 назв. Рис. 25.

УДК 517 (075.8) ББК 22.161я73

ISBN	© Уральский федеральный университет, 2013

2

1. Комплексныечисла

Кратко напомним понятие комплексных чисел и действий с ними.

1.1. Определение, изображение,

формы записи комплексного числа

Комплексным числом z

называют выражение вида

z x i y,

где x, y – дей-

ствительные числа, i − так называемая мнимая единица,

i2 1.

Комплексное число z x i y изображают точкой М плоскости с

M(x, y)

координатами x, y или ее радиус-вектором

OM (рис. 1). Длину

y

y

вектора OM называют модулем комплексного числа z

и обознача-

ют

z

или r :

0

x

x

Рис. 1

x2 y2.

z

r

OM

Угол между радиус-вектором OM и положительным направлением оси ох

называют аргументом комплексного числа z. Угол

определяется неодно-

значно, с точностью до слагаемого 2 k

k 0, 1, 2,... ;

то значение ,

которое

заключено между

и , обозначают argz

и называют главным значением ар-

гумента.

Наряду с алгебраической формой z x i y комплексного числа рассмотрим

еще две формы записи.

Так как x rcos ,

y rsin (рис.1),

то комплексное число

z x i y

можно

записать в тригонометрической форме:

z r cos isin .

Введя функцию

ei cos isin , комплексное число можно записать в показательной форме:

z r ei . Итак, имеем три формы записи комплексного числа

z x i y r cos isin r ei .

Пример 1.1. Записать комплексные числа z1 1 i

z2 1 i

в тригонометриче-

3,

ской и показательной формах.

Решение. Найдем модули и аргументы этих чисел:

arg 1 i

;

1 i

2,

argtg

3

3

3

1

3

1 i

arg 1 i argtg1

.

2,

4

i

i

4

Тогда z1 1 i 3 2 cos

isin

2e

3

,

z2

1 i

2 cos

isin

2e .

3

3

4

4

3

1.2.Действия с комплексными числами

1.При сложении (вычитании) двух комплексных чисел складываются (соответственно вычитаются) их действительные и мнимые части.

2.Умножение двух комплексных чисел в алгебраической форме определяется по правилам умножения двучленов с учетом равенства i2 1.

При умножении двух комплексных чисел в тригонометрической и показа-

тельной формах их модули умножаются, а аргументы складываются:

	z1 z2		z1		z2	,	arg(z1 z2) argz1 argz2	.

3. При делении двух комплексных чисел в алгебраической форме нужно числи-

тель и знаменатель дроби z1 умножить на число, сопряженное знаменателю. z2

При делении двух комплексных чисел в тригонометрической и показательной формах их модули делятся, а аргументы вычитаются, т.е.

	z			z1		,	argz argz	argz	2	.
				z2			1

4.Возведение в степень комплексного числа в алгебраической форме осуществляется по правилам возведения в степень двучлена с учетом того, что

i2 1,

i3 i2 i i,

i4 i2 i2 1 и т.д.

При возведении комплексного числа z в большую степень удобно использо-

вать его тригонометрическую или показательную формы:

zn rn (cosn i sinn ) rnein

.

5. При извлечении корня из комплексного числа z

удобно использовать три-

гонометрическую форму записи комплексного числа z r(cos isin ):

n

n

2 k

2 k

z

r cos

n

i sin

n

k 0,1,2,...,n 1.

Таким образом, корень степени n из комплексного числа z имеет

n различных значений.

1 i

Пример 1.2. Вычислить 1)

z40, если z

3

, 2) w

, 3) z

.

1 i

3

7 24i

1 i

Решение. 1). Воспользуемся примером 1.1 и учтем, что

1 i

z

1 i

3

3

2

2,

1 i

1 i

2

argz

1 3i

arg 1 3i arg 1 i

7

arg

.

1 i

3

4

12

4

Тогда		z40									40			220,										argz40													40argz																	7			40									70							,
								2
																																																			12														3
		z	40							20							70						isin									70									20																								2										isin												2
					2								cos																									2							cos 24																																				24
																	3																3																																3																							3
																	2													2																1
																																																										3
																																																																											1 i				3 .
					220								cos									isin															220														i											219
																	3														3															2										2
2). Из примера 1.1 следует, что
																																		1 i						3 2 cos																						isin													. Тогда
																																																								3													3
																																									/3 2 k																													/3 2 k
													w					1 i																																												isin
																									3								2					cos																																														.
																																																			2																										2
При k 0		и при k 1 получим два значения корня:
																																																									1
															/3													/3																					3																			2
		w																		isin																																																								3 i
						2						cos																												2														i																											,
		1													2																2																2									2									2
															/3 2																						/3 2																																							1
																																																																			3																		2
		w																								isin																																															i															3 i
						2						cos																																													2																																				.
		2															2																						2																										2											2					2

3). При извлечении корня из комплексного числа 7 24i использовать тригоно-

метрическую форму записи комплексного числа нерационально. Воспользуемся другим способом. Учтем, что 7 24i 16 9 24i 42 3i 2 2 4 3i 4 3i 2 . Тогда

z 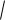7 24i 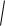4 3i 2 4 3i .

Замечание. Если Вы не смогли выделить полный квадрат в подкоренном вы-

ражении, то вычислить 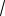7 24i можно по определению: 7 24i x i y , где x, y действительные числа. Для их отыскания возведём в квадрат обе части ра-

венства и приравняем действительные и мнимые части комплексных чисел:

		7 24i x i y 2							x2		2xyi y2						2	y		2	7,
																x
																xy 12.
Решим получившуюся систему уравнений
x2 y2 7,	y		12		, x	2	144				x	4	7x	2							x1	4,	y1	3,
										7					144 0
				x				x
xy 12,									2												x2	4,	y2	3.
Таким образом,				имеет два значения 4 3i												и 4 3i .
		7 24i
Пример 1.3. Решить уравнение z2 2 i z 7i 1 0.
											5

Решение. Воспользуемся формулой для вычисления корней квадратного урав-

нения и результатом предыдущего примера:

z	2 i (2 i)2 28i 4				2 i 7 24i							2 i (4 3i)2			2 i (4 3i)	,
1,2		2				2					2			2
	z		2 i 4 3i			3 i,	z			2 i 4 3i			1 2i.
								2
	1	2									2
Пример 1.4. Решить систему уравнений									(2 i)z1 (3 i)z2 4 2i,
									(5 2i)z1 (2 3i)z2 5i.

Решение. Воспользуемся при решении системы методом Крамера. Вычислим

определители:

2 i

3 i

2 i 2 3i 5 2i 3 i 12 19i,

5 2i

2 3i

1

4 2i

3 i

4 2i 2 3i 3 i 5i 7 31i,

5i

2 3i

2

2 i

4 2i

2 i 5i 4 2i 5 2i 19 12i .

5 2i

5i

Тогда

z

1

7 31i

7 31i 12 19i

505 505i

1 i,

12 19i

1

12 19i 12 19i

505

2

19 12i

19i2 12i

i

12 19i

z

2

i.

12 19i

12 19i

12 19i

Пример 1.5. Указать, какие линии определяются следующими уравнениями:

1) Rez2 1; 2) z z Rei ; 3)

z 3 2i

3; 4)

z 2i

z 2i

6, 5)

z 3 2i

z

.

0

Решение. 1). Выделим действительную часть функции z2 :

Rez2 Re x i y 2 Re x2

2xyi y2 x2 y2 .

Тогда уравнение Rez2 1 примет вид x2

y2 1. Это уравнение определяет рав-

ностороннюю гиперболу (a b 1) с центром в точке (0,0).

2). Запишем равенство z z0 Rei в виде:

x i y x0 i y0 R(cos isin ).

x x0

Rcos ,

z

Приравняем действительные и мнимые части:

Rsin .

y y0

z0

Рис.2

6

Если [0,2 ) , то эти уравнения определяют окружность x x 2 y y 2

R2

с

0

0

центром вточке x0, y0 радиуса R (рис.2); если 0, , то урав-

нения определяют верхнюю половину окружности.

z

3

Так как

z z0

есть расстояние точек

z от точки z0 и оно

-2

z0

постоянно (равноR), то уравнение окружности с центром в точке

z0 радиуса R можно записать и в другом виде

z z0

R.

Рис.3

Итак, уравнение окружности с центром в точке z0 радиуса R имеет вид

z z Rei , [0,2 )

или

z z

0

R.

0

3). Уравнение

z 3 2i

3 запишем в виде

z 3 2i

3; следовательно, оно

определяет окружность с центром в точке z0 3 2i

радиуса R 3 (рис. 3).

4). В уравнении

z 2i

z 2i

6 модуль

z 2i

есть расстояние точки z от

точки z0 2i, а модуль

z 2i

z 2i

есть расстояние точки z от

z

3i

точки

z1 2i . Следовательно,

уравнение

z 2i

z 2i

6

опреде-

z0

ляет множество точек z, сумма расстояний от которых до двух за-

данных точек z0 2i и z1 2i есть величина постоянная, равная 6 и

z1

большая, чем расстояние между z0

и

z1.

Такое множество точек

Рис. 4

есть эллипс с фокусами в точках z0,

z1,

причем длина оси эллипса,

на которой лежат фокусы, равна 6 (рис. 4).

z

5). В уравнении

z 3 2i

z

модуль

z 3 2i

есть расстояние

z1

точки

z

от точки

z0 3 2i, а модуль

z

z 0

есть расстояние

-2

точки

z

от точки

z1 0. Поэтому уравнение

z 3 2i

z

опреде-

Рис.5

ляет множество точек z

равноудаленных от точек z0 3 2i

и z1 0.

Это множество точек есть серединный перпендикуляр к отрезку z0z1

(рис. 5).

3

z0

2. Элементарныефункциикомплексногопеременного

Функции e z, sin z, cosz

Функции ez, sin z, cosz для любого действительного z определяются как суммы следующих рядов:

7

ez 1

z

z2

z3

z4

(2.1)

1!

2!

3!

4!

sin z

z

z3

z5

z7

(2.2)

1!

3!

5!

7!

cosz 1

z2

z4

z6

(2.3)

2!

4!

6!

Связь между функциями e z, sin z, cosz

cosz

eiz e iz

sinz

eiz e iz

eiz cosz isinz

,

,

.

(2.4)

2

2i

Эти формулы называют формулами Эйлера.

Свойства функций e z, sinz, cosz

1). e z1 z2 e z1 ez2 .

2). Функция e z

имеет период

T 2 i.

3). Функции sin z, cosz

имеют период T 2 .

4). Функция sin z − нечетная, функция cosz

– четная.

5). а) sin2 z cos2 z 1,

б) sin z

z

2

sin z

cosz

2

cosz

sin z

2

,

г)

sin2z 2sin z cosz ,

1

1

1

cos2z cos2 z sin2 z.

в) cos z

z

2

cosz

cosz

2

sin z

sin z

2

,

д)

1

1

1

6). Функции sin z, cosz

− не ограничены на комплексной плоскости.

Обратите внимание на то, что свойства I), 3), 4), 5) функций ez , sin z, cosz такие же, как для соответствующих функций действительной переменной. Свойства же 2) и 6) имеют место только для функций комплексной переменной.

Перечисленные свойства используются при вычислении значений функций e z, sin z, cosz и при решении уравнений, содержащих эти функции.

Пример 2.1. Вычислить eln5 3 i/2.
Решение. Воспользуемся свойством 1),			основным логарифмическим тожде-
ством и одной из формул (2.4):				3		3
eln5 3 i/2 eln5 e3 i/2					isin			5i .
	5	cos
			2		2

Гиперболические функции

Для комплексного аргумента гиперболические синус и косинус вводятся так же, как для действительного аргумента, т.е.

	shz ez e z	,	chz	ez e z		.	(2.5)
	2		2
Перечислим свойства функций sh z,			ch z .

1). Функции sh z, ch z имеют период 2 i (так же, как функция ez ).

2). Для комплексного аргумента существует следующая связь между тригонометрическими и гиперболическими функциями:

8

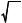
	cos iz chz,	sin iz ishz,	(2.6)
	ch iz cosz,	sh iz isinz.

3). Для комплексного аргумента (как и для действительного): ch2 z sh2 z 1,

sh z1 z2 sh z1 ch z2 ch z1 sh z2,

ch z1 z2 ch z1 ch z2 sh z1 sh z2,

	sh2z 2sh zch z,	ch2z ch2 z sh2 z.
			i
	Пример 2.2. Вычислить sin iln3 , ch 1			.
			2

Решение. Воспользуемся свойствами функций sinz, cosz, shz, chz :

sin iln3 sin cos iln3 cos sin iln3 sin iln3

i sh ln3 i

eln3 e ln3

i

3 1/3

4

i;

2

2

3

i

i

i

ish1 sin

ish1.

ch 1

ch1 ch

sh1 sh

ch1 cos

2

2

2

2

2

Логарифмическая функция

Ln z ln	z	i arg z 2 k ,	k 0, 1, 2,	(2.7)

Значение этой многозначной функции при k 0 называют главным значением логарифма и обозначают ln z .

На функцию Ln z распространяется ряд свойств логарифма действительного переменного:

I) Ln z z		Ln z Ln z		,	2) Ln		z1		Ln z Ln z
	2		2							2	,
1		1							1
3) Ln z1z2 z2 Ln z1,						z2
					4) eLnz z .

Обобщенные степенная и показательная функции

Степенная функция w z a с произвольным комплексным показателем a i определяется равенством

w z a eLnza e a Lnz

.

Показательная функция

w a z с произвольным комплексным основани-

ем a i определяется равенством

w a z eLna z

e z Lna

.

Пример 2.3. Вычислить 1) Lni,

2) 1i ,

1 i

2 i

3)

.

2

Решение. 1). Вычислим модуль и аргумент для z i:

i

1, argi / 2. Тогда

Lni ln1 i /2 2 k

i

1 2k

, k 0, 1, 2,....

2

9

Главное значение логарифма есть lni i /2.

2). Запишем w 1i

в виде w eLn1i

ei Ln1

ei (ln1 2 ki) e 2 k ,

k 0, 1, 2,.....

1

i

1, arg

1

i

3). Учитывая, что

2

, получим:

4

2

2

2

2i

1 i

2i

2i ln

1

i

Ln

i

2

2i

ln1 i

4

2

k

2

4 k

w

1

e

e

2 e

e

,

где k 0, 1, 2,...

2

Пример 2.4. Решить уравнение 4cosz 5 0.

Решение. Используя равенство cosz

eiz e iz

, запишем уравнение в виде

2

2(eiz e iz) 5 0.

Умножив это равенство на

eiz ,

получим 2e2iz 5eiz

2 0

или 2w2 5w 2 0 ,

где w eiz . Решения этого квадратного уравнения w 2,

w

1

,

т.е. eiz1 2 и

2

1

2

1 i

eiz2

1

. Прологарифмируем эти равенства и учтем, что

1

i :

i i

2

z1 1 2k iln2,

i

iz1 Ln( 2) ln2 i( 2 k),

k 0, 1, 2,...;

iz2

1

1

i ( 2 n) ln2 i (1 2n),

z2 1 2n iln2,

n 0, 1, 2,....

Ln

ln

2

2

Итак, можно решение уравнения записать в виде z (2k 1) i ln2,

k 0, 1, 2,...

Обратные тригонометрические и гиперболические функции

По определению

w Arcsin z, если sinw z;				w Arccosz, если cosw z ;
w Arctgz,	если tgw z ;			w Arcctgz , если ctgw z ;
w Arcsh z ,	если shw z ;			w Arcch z , если chw z ;
w Arcth z ,	если th w z;				w Arccth z , если cthw z.
Пример 2.5. Вычислить Arcsin i .
Решение.Изусловия Arcsin i z		имеем:
sinz i			eiz e iz		i eiz e iz 2 .
			2i

Умножив последнее равенство на eiz

e2iz 2eiz 1 0 eiz

Учтем, что

,получим

1 2 iz Ln 1 2 .

1			2			0						1						2						2		1,		arg 1		2		0;
																												arg 1				.
1			2			0					1						2						2		1,					2
Поэтому																i arg 1												2 k ln
iz1 Ln 1				ln				1																										1 2 ki;
	2												2														2						2
iz2 Ln 1					ln
										1 2 k i,																	k 0, 1, 2,...
		2							2
																				10