caplin_nikulin_modelirovanie_v_metallurgii

Гистограммой частот называют ступенчатую функцию, состоящую из прямоугольников, основанием которой служат частичные интервалы длиной h, а высоты равны отношению ni/h (плотность частоты).

Площадь i-го частичного прямоугольника hni / h = ni, т.е. сумме частот i-го интервала. Следовательно, площадь гистограммычастот равна сумме всехчастот, т.е. объему выборки.

Пример 2. Построить гистограмму частот (рис. 2.23) по распределению выборки объемом n = 100 в соответствии стаблицей:

Номер	Частичный интервал	Сумма	Плотность частоты
интервала	xi– xi+1	частот	ni/hi
1	1–5	10	2,5
2	5–9	20	5,0
3	9–13	50	12,5
4	13–17	12	3,0
5	17–21	8	2,0

Рис. 2.23. Гистограмма частот

2.9.Основы корреляционного

ирегрессионного анализа

Целью моделирования любого технологического процесса является установление количественной зависимости выходного параметра от одного или группы входных параметров, которые могут изменяться случайно. В функциональной связи Y = f (X)

каждому значению независимой переменной X отвечает одно вполне определенное значение зависимой переменной Y. Если

71

независимой переменной соответствует несколько значений Y, то связь между переменными X и Y приобретает статистический характер и называется корреляционной.

Простейшей и распространенной зависимостью между ве-

личинами X и Y является линейная регрессия. Оценка тесноты

или силы связи между величинами X и Y осуществляется мето-

дами корреляционного анализа.

Рассмотрим линейную регрессию от одного параметра (рис. 2.24). Пусть для произвольного фиксированного значения x получено несколько значений Y. Предполагается, что величина Y распределена нормально с математическим ожиданием

M y = k x + b

(2.49)

и дисперсией σ 2y , не зависящей от X. Примем, что случайная величина Y в среднем линейно зависит от фиксированного значения x, а параметры k, b и σ 2y являются неизвестными параметрами генеральной совокупности.

Рис. 2.24. Корреляционное поле зависимости Y = f (х) с эмпирической (1) и теоретической (2) линиями регрессии

Для оценки этих неизвестных величин по выборке объемом n сопряженных пар значений x1, y1; x2, y2; …; xn, yn в декартовой системе координат можно построить корреляционное

72

поле, содержащее n точек. Если нанести на поле средние значения yi , соответствующие всем значениям переменной xi, то зависимость y от x станет более очевидной.

Ломаная линия, соединяющая точки yi , отнесенные к се-

рединам интервалов xсрi, называется эмпирической линией регрессии. С увеличением числа опытов ломаная линия сглаживается и приближается к предельной линии – теоретической линии регрессии.

Метод наименьших квадратов

Для линейной зависимости линия регрессии задается уравнением прямой:

y = kx + b,

(2.50)

неизвестные коэффициенты которой определяются по методу наименьших квадратов. В соответствии с этим методом квадрат расстояния по вертикали между опытными точками с координатами xi, yi и соответствующими точками на линии регрессии должно быть минимальным:

n

(kx + b)

2

= min.

y −

(2.51)

∑ i

i

i=1

Из уравнений для определения неизвестных коэффициен-

тов k, b

∂

n

− (b + kx) 2

∂

n

y − (b + kx) 2

y

= 0,

= 0

(2.52)

∂

∑

i

∂ k

∑ i

b i=1

i =1

следует:

n

n

− b − kxi ) xi = 0,

∑( yi − b − kxi ) = 0,

∑( yi

(2.53)

i=1

i=1

откуда

n

n

n

n

n

∑ yi

= nb + k ∑ xi

, ∑ yi xi = b∑ xi

+ k ∑ xi2 .

(2.54)

i =1

i =1

i=1

i=1

i=1

73

1

n

1

n

1

n

Сучетом обозначений

=

∑ xi ,

=

∑ yi ,

x2 =

∑ xi2 ,

x

y

n i =1

n i=1

n i=1

1

n

=

∑ xi yi следует

xy

n i =1

b =

− kx

,

(2.55)

y

	n			n	n
	∑ xi yi	−	∑ yi ∑ xi			n
k =	i =1	i=1			i=1		=
	n			n	2
	∑ xi2 −			∑ xi		n
	i =1		i=1

	n
	∑( xi −		)( yi −				)
		x				y
	i=1							. (2.56)
	n
	∑( xi −				)2
				x
	i =1

Таким образом, уравнение линейной регрессии принимает

вид:

y = kx + b =

+ k ( x −

) .

(2.57)

y

x

Пример 1. Построить линейную зависимость регрессии по

семи экспериментальным точкам:

Значения аргумента, i

1

2

3

4

5

6

7

Значения функции, y

2,35

2,41

2,60

2,73

2,90

3,11

3,25

Решение.

n

7

n

7

=

1

∑ yi

=

1

∑ yi

=

19,35

= 2,764 ;

=

1

∑ xi =

1

∑ xi

= 4 .

y

x

n i =1

7 i=1

7

n i =1

7 i =1

По формуле (2.56)

n

7

∑( xi −

)( yi −

)

∑( xi − 4)( yi − 2, 764)

x

y

k =

i =1

=

i =1

= 0,157 .

n

7

∑( xi −

)2

∑( xi − 4)2

x

i =1

i=1

По формуле (2.57) получаем искомую зависимость:

y = y + k ( x − x ) = 2,764 + 0,157 ( x − 4) .

74

Выборочный коэффициент корреляции

Коэффициент корреляции является количественной мерой, учитывающей стохастическую долю колебаний yi относительно средней y под влиянием xi и вычисляется по формуле:

n

∑( xi − x )( yi − y )

r =	i=1			,
		(n −1) σ σx
			y

где σx и σy – стандартные отклонения:

	n					n
	∑( xi	−		)2		∑( yi	−		)2
σ x=			x		, σ y=			y
	i =1					i=1	.
	n −1					n −1

(2.58)

(2.59)

Коэффициент корреляции не может быть использован для оценки технологической важности фактора. Его величина указывает только на тесноту связи между переменными, а знак – на характер влияния. Значения коэффициента корреляции находятся в пределах −1 ≤ r≤ 1:

при r < 0 – увеличение x вызывает уменьшение y; при r > 0 – увеличение x вызывает увеличение y;

при | r | = 1 – связь между x и y линейная функциональная; при | r | = 0 – корреляционной связи между x и y нет, или

она нелинейная.

Если выражение (2.58) преобразовать к виду:

n

∑( xi − x )( yi − y ) = r σ σx y (−n 1)

i=1

иподставить в формулу (2.56), то получим

	n
	∑( xi −		)( yi −		)
		x		y			r σ σx y (−n 1)		σr σ x		σ= r
k =	i =1					=		=		y
	∑( xi − x )2								σ x
							∑( xi − x )2				σ
	n						n		2
	i=1						i =1

(2.60)

y . (2.61)

x

75

Отсюда видна непосредственная связь коэффициента корреляции r и коэффициента k в уравнении линейной регрессии, их знаки всегда совпадают.

Выражения (2.58), (2.59) выражают тесноту и вид связи между переменными x и y.

2.10.Вопросы для самоконтроля

1.Сформулируйте основные причины появления неопределенностей. Какие из них являются субъективными, а какие – объективными?

2.Как описывается неопределенность математически?

3.Приведите примеры математического описания неопределенностей в металлургии.

4.Когда в задаче математического моделирования применяется стохастическое описание переменных?

5.Дайте определение функции и плотности распределения.

6.Меры положения и рассеяния кривой распределения. Объясните различие между модой, медианой и математическим ожиданием.

7.Что характеризуют дисперсия, стандартное отклонение, коэффициент корреляции?

8.Дайте характеристики законам распределения: нормальному, экспоненциальному, равномерному.

9.Что характеризуют начальный и центральные моменты?

10.Квантили распределения.

11.Интервальные оценки, доверительные интервал и вероятность.

12.Ошибки диагностирования первого и второго рода, их значение.

13.Способы представления параметров распределения: эмпирическая функция распределения, полигон частот, гистограмма частот.

14.Что такое корреляционное поле, линии регрессии?

15.Метод наименьших квадратов для получения уравнения линейной регрессии.

16.Коэффициент корреляции, его смысл.

76

3. Математические модели теплофизики металлургических процессов

сдетерминированными структурами

3.1.Законы конвективного тепломассообмена

Процессы конвективного тепло- и массообмена происходят в результате движения теплоносителя (жидкости или газа) и всегда тесно связаны с соответствующими процессами молекулярного переноса (теплопроводностью и диффузией).

В зависимости от причины движения теплоносителя различают конвекцию вынужденную и свободную (естественную). Впервом случае движение теплоносителя обусловлено внешними причинами: насосом, вентилятором, компрессором и т.п. Во втором случае движение теплоносителя вызвано неоднородностью температур или концентраций компонент теплоносителя.

Конвективная теплоотдача играет важную роль при нагреве металла в печах, при химико-термической обработке металла, формировании слитка. При этом, как правило, основную роль играет вынужденная конвекция, однако и свободно конвективный теплообмен определяет теплоотдачу от нагретых поверхностей в окружающую среду.

При конвективном тепломассообмене перенос теплоты неразрывно связан с переносом массы. Если текучая среда плотностью ρ [кг/м3] движется в направлении оси x со скоростью ux [м/с], то ее массовая скорость характеризует массу среды, проходящей в единицу времени через единичную площадку

ρ ux

кг м

кг

.

(3.1)

3

с

2

м

м

с

Теплосодержание среды может быть выражено через

удельную теплоемкость

c Дж (кг К)

и температуру Т:

Дж К

Дж

cT

.

(3.2)

кг

К

кг

77

Плотность теплового потока, определяемая конвекцией, равна произведению массовой скорости на теплосодержание:

q

= ρ u

cT

кг Дж

Вт

.

(3.3)

2

к

x

с кг

м

2

м

Конвекция всегда сопровождается теплопроводностью, поэтому общая плотность теплового потока при конвективном тепломассообмене с учетом закона теплопроводности Фурье имеет вид:

q = qт + qк = −λ T+ ρ cT u .

(3.4)

Конвективный теплообмен между потоком текучей среды и поверхностью соприкасающегося тела называется теплоотдачей (рис. 3.1). При расчетах теплоотдачи используют закон Ньютона – Рихмана:

dФ = α (Tп− Tc )dS, [Вт] ,

(3.5)

в котором разность между температурой поверхности тела (Тп) и температурой окружающей среды (Тc) называют температур-

ным напором; α – коэффициент теплоотдачи;

α =	dФ dS		,	Вт
						.	(3.6)
	T − T				м2 К
	п	c

Рис. 3.1. Схема теплоотдачи

78

Коэффициент теплоотдачи характеризует плотность теплового потока на границе текучей среды и соприкасающегося с ней тела, отнесенную к температурному напору.

Таким образом, плотность теплового потока при конвективном теплообмене между поверхностью тела и окружающей средой определяется уравнением теплоотдачи:

q = α	(T −	T ), [Вт / м2	] .	(3.7)
к	п	c

Аналогичное уравнение описывает массоотдачу. При этом плотность потока массы i-го компонента смеси определяется суперпозицией концентрационной, термо- и бародиффузии:

∂ Ci

DT ∂ T

Dp ∂

p

qmi

= − D

+

+

,

(3.8)

∂ n

T ∂ n

p∂

n

где DT , Dp

– коэффициенты термо- и бародиффузии,

DT = kT D,

Dp = k p D ;

kT , k p

– термо-

и бародиффузионные отношения,

kT = DT 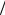D , k p = Dp D .

Коэффициент пропорциональности D характеризует концентрационную диффузию и называется коэффициентом концентрационной диффузии

D =

qmi

кг м4

м2

,

.

(3.9)

∂ Ci

∂ n

2

с кг

с

м

Коэффициент концентрационной диффузии (коэффициент диффузии) характеризует плотность потока массы i-го компонента смеси при единичном градиенте концентрации примеси.

Термодиффузия происходит в смеси с неоднородной температурой: более тяжелые молекулы стремятся перейти в холодные области (эффект Соре).

Бародиффузия происходит в смеси с неоднородным давлением: тяжелые молекулы стремятся перейти в область повышенного давления.

79

При равенстве молекулярных масс компонентов смеси термо- и бародиффузия отсутствует, основную роль играет концентрационная диффузия, соотношение (3.8) переходит

взакон Фика.

3.2.Уравнения конвективного тепломассообмена

Дифференциальное уравнение неразрывности

Дифференциальное уравнение неразрывности (сплошности) вытекает из закона сохранения массы текучей среды и накладывает, поэтому, ограничения на скорости течения. Этот закон постулирует следующее: изменение массы контрольного объема в некоторый промежуток времени течения среды должно компенсироваться изменением ее плотности за этот же промежуток времени. Вывод уравнения рассмотрим на примере одномерного течения в канале (рис. 3.2).

Рис. 3.2. Расчетная схема к выводу уравнения неразрывности

В некотором сечении канала x с площадью поперечного сечения f среда объемом fdx плотностью ρ течет со скоростью u в направлении возрастания координаты x. Используя понятие массовой скорости ρ u, кг/(м2 с), запишем расход массы за время dτ через левую и правую грани контрольного объема:

dmx = (ρ u )x f dτ , dmx+dx = (ρ u )x+dx f dτ .

80