3.4. Отключение постоянного напряжения

от последовательной цепи RL

Пусть в моментt = 0 постоянное напряжение U отключается от последовательной RL-цепочки путём простого разрыва. При t < 0 в катушке был ток i = U/R. При разрыве цепи он скачком должен упасть до нуля, однако это противоречит второму уравнению Кирхгофа. В этой ситуации происходит следующее.

При размыкании ключа К сопротивление его контактов r_к резко возрастает, что приводит к очень быстрому уменьшению тока в цепи – быстрому, но не скачкообразному. При этом резко возрастает и ЭДС самоиндукции катушки: Е_с.и=, причём это возрастание настолько велико, что при разрыве контактов ключаК между ними происходит электрический пробой – искра. И этот пробой будет при любой скорости размыкания ключа, так как чем быстрее размыкание, тем больше di/dt, а, следовательно, и тем больше ЭДС самоиндукции.

Замечание 1. Этот пробой может произойти не только в ключе К, но и в межвитковой изоляции самóй катушки, что приведёт катушку в негодность.

Замечание 2. Итак, при разрыве цепи с индуктивностью Е_с.и катушки во много раз превышает разорванное внешнее напряжение U, и в связи с этим, эта ЭДС очень опасна для человека.

Напряжения на элементах цепи, превышающие напряжение, приложенное от генератора, называются перенапряжениями.

В связи с возникновением опасных перенапряжений, катушки с большими индуктивностями (L≥1 Гн) нельзя отключать от генератора по приведённой выше схеме, т.е. путём простого разрыва цепи. Обычно ток в таких цепях сначала плавно уменьшают до нуля каким-либо регулятором, а потом уже разрывают цепь (например, на ГЭС).

Но можно сделать и быстрое отключение генератора от RL-цепи, если параллельно ей поставить активное сопротивление R₀. Рассмотрим переходный процесс в цепи RLR₀ после отключения от неё постоянного напряжения U.

При t > 0 второе уравнение Кирхгофа для указанного контура будет таким:

, или , (7)

или , где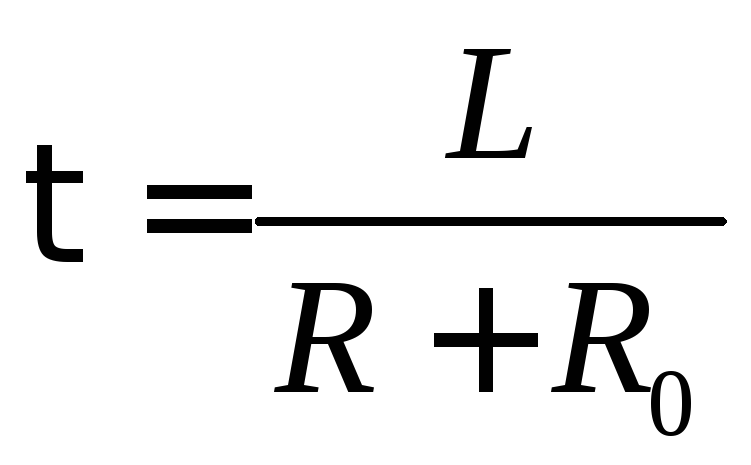

Его решение: i = .

Из начального условия следует, что, и тогда

.

Напряжение на резисторе R₀ (т. е. на выводах катушки RL) в этом случае

и_кат=.

Если R₀≫R, то в первый момент после размыкания ключа К это напряжение может быть очень велико: .

Пример. Пусть R = 10 Ом – это активное сопротивление обмотки катушки,

R₀ = 50 кОм – сопротивление взявшегося за катушку человека,

U =1 В – напряжение отключаемой от катушки батарейки.

Тогда при t = +0 напряжение и_чел=кВ.

Запасённый катушкой ток=100 мА будет «прокачан» через человека во что бы то ни стало. Однако, эффективный импульс тока будет очень короток: например, приL=1 Гн длительность импульса 20 мкс.

Замечание. Если при t < 0 был ток i₀, а сопротивления , то при отключении катушки от генератора она будет сохранять этот ток бесконечно долго. Действительно, так как приуравнение (7) принимает видL(di/dt) = 0, то i = const = i₀. Вместе с током катушка сохраняет и энергию .

4. Переходные процессы в одноконтурной цепи 2-го порядка

4.1. Отключение постоянного напряжения

от последовательной цепи RLС

Пусть в моментt = 0 постоянное напряжение U отключается от последовательной цепи RLС, так что при t > 0 она образует замкнутый последовательный контур.

Т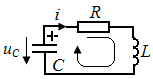ак как приt < 0 тока в контуре не было, а конденсатор был заряжен до напряжения U, то начальные условия переходного процесса будут такими:

i(+0) = i(−0) = 0, и_С(+0) = и_С(−0) = U. (1)

После замыкания контура конденсатор начнёт разряжаться, в контуре пойдёт ток i и начнётся свободный процесс, характер которого зависит от соотношения между параметрами R, L и С. Расставив стрелки тока и обхода, запишем второе уравнение Кирхгофа:

u_L + u_R − u_C = 0, или . (2)

Дифференцируя (2) и учитывая, что при данной расстановке стрелок , получаем уравнение 2-го порядка относительно токаi:

, (3)

где − коэффициент затухания,− собственная частота.

Запись уравнения 2-го порядка в канонической форме (3) удобна тем, что его решение выражается простыми и наглядными функциями параметров β и ω₀.

Подстановкой

(4)

оно сводится к более простому уравнению (проверить самостоятельно):

, (5)

решение которого хорошо известно и зависит от соотношения между β и ω₀. Здесь возможны три варианта:

Вариант 1: >0 (колебательный вариант).

Обозначив = ω², получим:

.

Как известно, общим решением этого уравнения является функция

.

И тогда, с учётом (4), получаем:

. (6)

Коэффициенты А и В здесь зависят от начальных условий. Для дифференциального уравнения 2-го порядка должны быть заданы два начальных условия: ток i и его первая производная в момент t = 0. Здесь следует помнить, что начальные условия для всякого переходного процесса задаются именно при t =+0, а не при t = −0, т. е. в первый момент после коммутации в цепи. А условия при t = +0 определяются уже правилами коммутации:

1) ток через индуктивность скачком измениться не может;

2) напряжение на конденсаторе скачком измениться не может.

Подстановка 1-го начального условия i(+0) = i(−0) = 0 в (6) даёт: В=0, т. е.

. (7)

Второе начальное условие следует из уравнения (2): так какi(0) = 0, а и_С(0) = U, то . Но, в силу (7),. Следовательно,. И тогда для тока в контуре получаем:

. (8)

Кривая (8) описывает свободные затухающие колебания в последовательной цепи RLC. Она, в строгом смысле, не периодична, но периодически и бесконечное число раз проходит через ноль с периодом , где.

Напряжения на элементах контур также будут носить характер затухающих колебаний. В частности, напряжение на конденсаторе теперь легко можно найти из уравнения (2): и_С(t) =, напряжение на резистореu_R(t) = iR.

Вариант 2: (критический вариант).

Уравнение (5) в этом случае принимает вид:

,

и его решение . Следовательно, для токаi, с учётом (4), получаем:

.

Из тех же начальных условийi(0) = 0, получаем:В=0, . И тогда

. (9)

Полученная функция является апериодической. Сопротивление R, при котором колебательный процесс вырождается в апериодический, называется критическим сопротивлением R_кр. Величина этого сопротивления определяется из условия :R_кр=.

Закон изменения напряжения на конденсаторе теперь проще всего определить из соотношения и_С(t) =с учётом найденного тока (9):

.

Вариант 3: β² >(закритический вариант).

Обозначив , получим:

.

Общее решение этого уравнения имеет вид:

.

Следовательно, ток

, (10)

где . При тех же начальных условиях, что и предыдущих вариантах, ток в этом случае будет таким:

, (11)

где .

Зависимость (11) качественно совпадает с вариантом 2, т. е. процесс здесь также будет апериодическим и экспоненциально затухающим, так как показатели в обеих экспонентах (10) отрицательны. Графики i(t) и u_C(t) здесь такие же, как и в предыдущем варианте, только с ещё большим затуханием.

Ситуация β² >реализуется приR>R_кр=.