АППРОКСИМАЦИЯ ФУНКЦИЙ

Слово «аппроксимация» происходит от латинского approximo — приближаюсь. Аппроксимировать – это означает приближенно заменить. Задачи интерполяции возникают при обработке результатов экспериментов, когда измерения какойлибо величины выполнены в конечном числе точек. Требуется найти промежуточные значения этой функции. Это так называемая задача о восстановлении функции. Кроме того, при проведении расчетов сложные функции удобно заменять (аппроксимировать) алгебраическими многочленами или другими элементарными функциями, которые достаточно просто вычисляются (задача о приближении функции).

Методы интерполяции используются для приближенного интегрирования и решения дифференциальных уравнений, а также являются основой компьютерной графики и других современных цифровых технологий.

Постановка задачи интерполяции
На интервале a,b заданы точки xi , i 0,1,..., N ; a xi b ,
и значения неизвестной функции			в	этих точках	f xi fi ,
i 0,1,..., N . Требуется найти функцию F x , принимающую в
точках xi те же значения fi . Точки			xi	будем называть узлами
интерполяции,	а	условия	F	xi fi –	условиями
интерполяции.	При этом F x будем искать только на отрезке

a,b . Если необходимо найти функцию вне отрезка, то такая

задача называется задачей экстраполяции. Мы будем рассматривать только задачи интерполяции.

Поставленная задача имеет много решений, т.к. через
заданные точки xi , fi ,	i 0,1,..., N , можно провести

бесконечно много кривых, каждая из которых будет графиком функции, для которой выполнены все условия интерполяции. Для практики важен случай аппроксимации функции

41

многочленами, т.е. F x a	0	a x a	2	x2	... a	m	xm ,	где a	i	–
		1

постоянные коэффициенты.

Все методы интерполяции можно разделить на локальные

и глобальные. В случае локальной интерполяции на каждом интервале xi 1 , xi строится отдельный полином. В случае

глобальной интерполяции отыскивается единый полином на всем интервале a,b . При этом искомый полином называется

интерполяционный полиномом.

Локальная интерполяция

Кусочно-постоянная интерполяция

При кусочно-постоянной интерполяции интерполяционный многочлен на каждом отрезке xi 1 , xi равен константе, а

именно, левому или правому значению функции.

Для левой кусочно-постоянной интерполяции F x fi 1 , если xi 1 x xi , т.е.

f	0	,	x		0	x x
						1
f1 ,			x1			x x2		.
F x
...
			,		xN 1 x xN
f N 1
Для правой			кусочно-постоянной интерполяции F x fi ,
если xi 1 x xi			, т.е.
f	1	,	x	0		x x
						1
f	2 ,		x1			x x2	.
F x
...
			xN 1 x xN
f N ,
Легко понять,					что при таком выборе функции F x условия

интерполяция выполняются. Однако, построенная функция является разрывной, что ограничивает ее применение.

42

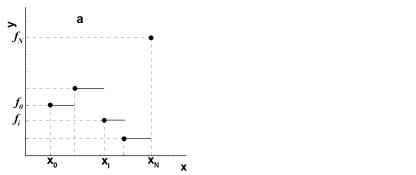
Графическое представление для кусочно-постоянной интерполяции можно увидеть на рис. 3.1.

Рис. 3.1. Левая (а) и правая (б) кусочно–постоянная интерполяции

Кусочно-линейная интерполяция

На каждом интервале xi 1 , xi интерполирующая функция является линейной Fi x ki x li . Значения коэффициентов ki и li находятся из выполнения условий интерполяции на концах

отрезка xi 1 , xi : Fi xi 1 fi 1 , Fi xi fi . С помощью этих условий получаем систему уравнений:

ki xi 1 li fi 1 ,

ki xi li fi

li fi	fi fi 1	xi .
	xi xi 1

записать в виде:

откуда

находим

ki

Следовательно, функцию F x

	F x	fi fi 1	x xi fi , если	xi 1	x xi , т.е.
		xi xi 1

	fi fi 1	,
	xi xi 1

можно

43

f1 f0

x x

f

,

x

x x

,

0

0

0

x1

x0

1

f2

f1

x x1 f1 ,

x1

x x2

.

F x

x2 x1

...

f N 1

f N

x x

N

1

f

N

1

,

x

N 1

x

x

N

x

x

N1

N 1

При использовании линейной интерполяции сначала нужно

определить интервал,

в который попадает значение x , а затем

подставить его в формулу.

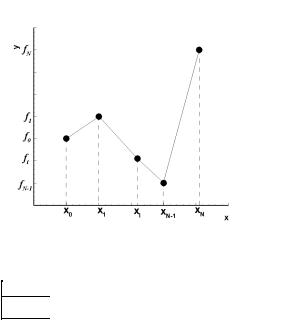
Итоговая функция является непрерывной, но ее производная разрывна в каждом узле интерполяции. Погрешность такой интерполяции будет меньше, чем в случае кусочно-постоянной интерполяции. Иллюстрация кусочнолинейной интерполяции приведена на рис. 3.2.

Рис. 3.2. Кусочно-линейная интерполяция

ПРИМЕР 3.1 Заданы значений некоторой функции:

x	0	2	3	3,5
f	-1	0.2	0,5	0,8

44