Моделирование биологических систем Модель однородной популяции

X(i+1) = x(i)+ax(i)-bx(i)²; x0 = c, i = 0.1...n, (3.82)

где n предельное время моделирования.

Усложнение модели может быть выполнено за счет учета переменности коэффициентов - a (скорости роста) и b (скорости гибели) - в зависимости от времени, а также с учетом половых, возрастных различий индивидумов.

Модель межвидовой конкуренции

dN1/dt=r1*N1(K1-N1-a12*N2)/k1

dN2/dt=r2*N2(K2-N2-a21*N1)/k2

где k1,k2 плотности насыщения

r1,r2 врожденные скорости роста

a12,a21- коэффициенты конкуренции

Эпидемия болезней

В изолированном поселке с населением m человек возникла эпидемия болезни, распространение которой описывается соотношениями:

xi+1 = xi – b*xi*yi;

yi+1 = yi - cyi + bxi*yi;

zi+1 = zi + cyi;

x0=a0, y0=b0, z0=c0,

где xi, yi, zi - число здоровых, больных (инфицированных) и невосприимчивых (переболевших) в момент времени i=0.1...n;

b - частота контактов больных и здоровых;

c - величина, обратная среднему времени выздоровления и зависящая от эффективности лекарств 0<L<1.

Более строго соотношение может быть получено из системы дифференциальных уравнений:

Модель “хищник - жертва”

Имеются популяции двух видов, которые представляются отношениями

xi+1 = xi + a1xi - b1xi2 - g1xiyi , x0 = c1,

yi+1 = yi - a2yi + b2yi2 - g2xiyi , y0 = c2,

где xi - численность (плотность) жертв,

yi - численность хищников,

g1 - коэффициент защиты жертв,

g2 - коэффициент прожорливости хищников.

Рост опухоли

Раковая опухоль обычно увеличивается экспоненциально в соответствии с дифференциальным уравнением:

, где v - размер опухоли,

с,a,b - константы.

Определить, при каких значениях параметров С существует предельный размер опухоли. Выяснить, при каких значениях С рост опухоли не превосходит некоторой конечной величины.

1.Изучить характер эволюции популяции, при зна­чениях параметров a,b,nв зависимости от значения параметраb в диапазоне 0,1 <b <10,

Есть ли качественные различия в характере эволюции в зависимости от значе­ния b?

2. Изучить характер эволюции популяции при зна­чениях параметров b,a, nв зависимости от значения параметраa в диапазоне 1 <a <10,

Есть ли качественные различия в характере эволюции в зависимости от значе­ния a?

3.Изучить характер эволюции популяцииа,b,vв зависимости от значения параметраV в диапазоне 1 <v<10.

Есть ли качественные различия в характере эволюции в зависимости от значе­ния v?

4.Реализовать модель при различных наборах значений параметров:n, a, b и изучить влияние параметров на характер эволюции.

5.Для модели в фазовой плоскости(b, a)найти границы зон, разделяю­щих режимы монотонного и колебательного установления стационарной числен­ности популяции изучаемой системы.

6.Для модели в фазовой плоскости(a,b)найти границы зон, разделяю­щих режим колебательного установления стационарной численности популяции изучаемой системы и режим устойчивых предельных циклов.

7.Реализовать моделирование межвидовой конкуренции по формулам при значениях параметровr1 =2,r2= 2,k1 =200,k2 =200,a12=0,5,a21= 0,5.Проана­лизировать зависимость судьбы популяций от соотношения значений их началь­ной численностиn1,n2.

8.Реализовать моделирование межвидовой конкуренции по формулам при значениях параметровr1 =2,r2= 2,k1 =200,k2= 200,a12= 100,a21 = 100. Проанализировать зависимость судьбы популяций от соотношения значений ко­эффициентов конкуренцииa12,a21,.

9. Построить в фазовой плоскости(n1n2) границы зон, разделяющих какие-либо два режима эволюции конкурирующих популяций (в соответствии с моделью ). Остальные параметры модели выбрать произвольно. Учесть при этом, что режим устойчивого сосуществования популяций может в принципе реализовать только при ф12 < 1.

10.Провести моделирование динамики численности популяций в системе «хищник-жертва» при значениях параметровr = 5, a= =0,q= 2c= 0,6 Проанализировать зависимость исхода эволюции от соотношения значений пара­метровn,c0.

11. Провести моделирование динамики численности популяций в системе «хищ­ник—жертва» при значениях параметровr= 5,а= 0,1,q= 2,f=100, Со = 6. Проанализировать зависимость результатов моделирования от значения параметраaв диапазоне 0,1 : 2.

12. Провести моделирование динамики численности популяций в системе «хищ­ник—жертва» при значениях параметровr = 5, а= 0,1,f= 2,N =100,

13. Провести моделирование динамики численности популяций в системе «хищ­ник—жертва» при значениях параметрова= 0,!f= 2,q =2,N= 100, Со=б. Проанализировать зависимость результатов моделирования от значе­ния параметраrв диапазоне 0,1 <r <2.

14.Провести моделирование динамики численности популяций в системе «хищ­ник—жертва» при значениях параметровa,q, No ,Co. Проанализировать зависимость результатов моделирования от значе­ния параметра «а» в диапазоне 0,1 <а <2.

15. Модель «хищ­ник—жертва» предсказывает сопряженные колебания численности жертв и хищников. Исследовать зависимость запаздывания амплитуд колебаний числен­ности хищников от амплитуд колебаний численности жертв в зависимости от значений параметраа.Значения остальных параметров фиксировать по усмотре­нию.

16.Модель «хищ­ник—жертва» предсказывает сопряженные колебания численности жертв и хищников. Исследовать зависимость запаздывания амплитуд колебаний числен­ности хищников от амплитуд колебаний численности жертв в зависимости от значений параметраq.Значения остальных параметров фиксировать по усмотре­нию.

17.Модель предсказывает сопряженные колебания численности жертв и хищников. Исследовать зависимость запаздывания амплитуд колебаний численно­сти хищников от амплитуд колебаний численности жертв и зависимости от значе­ний параметраa. Значения остальных параметров фиксировать по усмотрению.

18.Модель предсказывает сопряженные колебания численности жертв и хищников. Исследовать зависимость запаздывания амплитуд колебаний численно­сти хищников от амплитуд колебаний численности жертв в зависимости от значе­ний параметраf, Значения остальных параметров фиксировать по усмотрению.

19.Модель предсказывает сопряженные колебания численности жертв и хищников. Исследовать зависимость запаздывания амплитуд колебаний численно­сти хищников от амплитуд колебаний численности жертв в зависимости от соот­ношения значений начальных численностей популяцииN0, С0. Значения осталь­ных параметров фиксировать по усмотрению.

2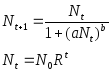3.Промоделировать процесс распространения инфекции стригущего лишая по участку кожи размером n*n (п —нечетное) клеток.

1.Внутривидовая конкуренция в популяции с

дискретным размножением Одна из центральных задач при моделировании случайных процессов — на­хождение характеристик случайных величин, являющихся объектом моделирова­ния. Главная такая характеристика — функция распределения. Ее вид можно каче­ственно оценить по гистограмме, построенной в ходе моделирования, а гипотезу о функциональной форме.Однако это не всегда целесообразно, особенно если в задаче требуется определить лишь неко­торые характеристики случайной величины — чаще всего среднее значение и дис­персию. Их можно найти без моделирования самой функции распределения проверить с помощью одного из стандартных критериев, используемых в математической статистике. При этом статистическая оценка достоверности результатов является обязательной.

Результаты моделирования уместно выводить на экран компьютера в следую­щем виде: в виде таблиц значений рассчитываемой величины (как правило, в нескольких выборках), в виде гистограмм распределения случайных величин, по­строенных в ходе моделирования.

Целесообразно там, где это возможно, сопровождать имитационное модели­рование визуальным отображением соответствующего процесса на экране компь­ютера (процесс формирования очереди, рождение и исчезновение объектов в за­дачах моделирования популяций и т.д.).

Моделирование случайных процессов

1.Провести моделирование очереди в магазине с одним продавцом при равнове­роятных законах распределения описанных выше случайных величин: прихода по­купателей и длительности обслуживания (при некотором фиксированном наборе параметров). Получить устойчивые характеристики: средние значения ожидания в очереди покупателем и простой продавца в ожидании прихода покупателей. Оце­нить их достоверность. Оценить характер функции распределения величинgи h.

2.Провести то же моделирование при пуассоновских законах распределения ве­роятностей входных событий: прихода покупателей и длительности обслуживания (при некотором фиксированном наборе параметров).

3.Провести то же моделирование при нормальном законе распределения вероят­ностей входных событий: прихода покупателей и длительности обслуживания (при некотором фиксированном наборе параметров).

4.В рассмотренной выше системе может возникнуть критическая ситуация, когда очередь неограниченно растет со временем, В самом деле, если покупатели заходят в магазин очень часто (или продавец работает слишком медленно), очередь начинает расти, и в рассматриваемой системе с конечным временем обслуживания наступит кризис. Построить зависимость между величинами (a max, b min), отражающую границу указанной критической ситуации, при равновероятном распределении входных событий.

5.На междугородней телефонной станции две телефонистки обслуживают общую очередь заказов. Очередной заказ обслуживает та телефонистка, которая первой освободилась. Если обе в момент поступления заказа заняты, то звонок аннулиру­ется и требуется звонить снова. Смоделировать процесс, считая входные потоки пуассоновскими.

6.Смоделировать ситуацию, описанную в предыдущем варианте, но считать, что, если в момент попытки сделать заказ обе телефонистки занять;, формируется очередь.

7.Пусть на телефонной станции с одним входом используется обычная система: если абонент занят, то очередь не формируется и надо звонить снова. Смоделиро­вать ситуацию: три абонента пытаются дозвониться до одного и того же владельца номера и в случае успеха разговаривают с ним некоторое (случайное по длитель­ности) время. Какова вероятность того, что некто, пытающийся дозвониться, не сможет сделать это за определенное время Т?

8.Смоделировать ситуацию, описаннуювпредыдущем варианте, но считать, что, если в момент попытки связаться телефон абонента занят, формируется очередь.

9.На травм. пункте работает один врач. Длительность лечения больного и проме­жутки времени между поступлениями больных — случайные величины, распреде­ленные по пуассоновскому закону. По тяжести травм больные делятся на три кате­гории, поступление больного любой категории — случайное событие с равноверо­ятным распределением. Врач вначале занимается больными с максимально тяже­лыми травмами (в порядке их поступления), затем, если таковых нет, — больны­ми с травмами средней тяжести (в порядке их поступления) и лишь затем — боль­ными с легкими травмами. Смоделировать процесс и оценить средние времена ожидания в очереди больных каждой из категорий,

10.Смоделировать ситуацию, описанную в предыдущем варианте, при условии, что в травм. пункте работают два врача, а больные делятся не на три, а на две категории.

11.Одна ткачиха обслуживает группу станков, осуществляя по мере необходимос­ти краткосрочное вмешательство, длительность которого — случайная величина.Какова вероятность простоя сразу двух станков? Как велико среднее время про­стоя одного станка?

12.Смоделировать ситуацию, описанную в предыдущем варианте, если группу стан­ков совместно обслуживают две ткачихи.

13.В городском автохозяйстве две ремонтные зоны. Одна — обслуживает ремонты краткой и средней продолжительности, другая — средней и долгой (т.е. средне­срочный ремонт может осуществлять каждая из зон). По мере поломок в автохо­зяйство доставляют транспорт; промежуток времени между доставками — случай­ная пуассоновская величина. Продолжительность ремонта — случайная величина с нормальным законом распределения. Смоделировать описанную систему. Каковы средние времена ожидания в очереди транспорта, требующего соответственно крат­косрочного, среднесрочного и длительного ремонта?

14.Реализовать имитационную модель статистического моделирования для реше­ния задачи Бюффона (XVIII в.). Автор аналитически нашел, что если на поле, разграфленное параллельными прямыми, расстояние между которымиL,броса­ется наугад игла длиной l, то вероятность того, что игла пересечет хотя бы одну прямую, определяется формулойр= 2*l/(pi*L) .

Эта задача дала способ имитационному определению числа pi. Действительно, если L =2*l, тоp= 1/pi. В ходе моделирования выполнить этот расчет.

15. Разработать модель случайного одномерного блуждания (модель «пьяницы»). Блуждание задается по правилу: если случайное число из отрезка [0,1] меньше 0,5, то делается шаг вправо на расстояниеh,в противном случае ~ влево. Распределе­ние случайных чисел принять равновероятным. Решить задачу: какова вероятность при таком блуждании удалиться от началь­ной точки напшагов?

16.В условиях задачи из предыдущего варианта получить ответ на вопрос: какова вероятность «пьяницей вернуться черезпшагов в начальную точку?

17.Точка хаотически блуждает на плоскости по узлам квадратной сетки с возмож­ностью делать с равной вероятностью шаги влево-вправо-вверх-вниз на фиксиро­ванный (за один ход) шаг. Движение происходит в замкнутом прямоугольном объе­ме, и при соприкосновении со стенкой происходит зеркальное отражение от нее.

Ответить в ходе моделирования на вопрос: как связана частота посещения каж­дого узла с расстоянием от него до того узла, из которого начинается движение?

18.Смоделировать ту же ситуацию, что и в задании к варианту 17, при условии неограниченной области блуждания и ответить на заданный вопрос,

19.Смоделировать полет пчелы. На плоскости (поляне) случайным образом растут медоносные растения с заданной концентрацией (на 1 м3). В центре — улей, из кото­рого вылетает пчела. Пчела может долететь от одного растения до любого другого растения, но вероятность выбора монотонно уменьшается с увеличением расстояния между растениями (по некоторому закону). Какова вероятность посещения пчелой конкретного заданного растения за заданное количество элементарных перелетов?

20. Реализовать модель плоского броуновского движенияпчастиц в прямоугольни­ке. Частицы считать шариками конечного размера. Удары частиц друг о друга и о стенки моделировать как абсолютно упругие. Определить п этой модели зависи­мость давления газа на стенки от числа частиц.

21.Разработать в деталях и реализовать модель перемешивания (диффузии) газов в замкнутом сосуде. В начальный момент времени каждый газ занимает половину сосуда. Изучить с помощью этой модели зависимость скорости диффузии от раз­личных входных параметров,

22.Реализовать имитационную модель системы «хищник—жертва» по следующей схеме.

«Остров» размером 20^20 заселен дикими кроликами, волками и волчицами, Имеется по несколько представителей каждого вида. Кролики в каждый момент перемещаются с одинаковой вероятностью 1/9 передвигаются в один из восьми сосед­них квадратов (за исключением участков, ограниченных береговой линией) или просто сидят неподвижно. Каждый кролик с вероятностью 0,2 превращается в двух кроликов. Каждая волчица передвигается случайным образом, пока в одном из соседних восьми квадратов не окажется кролик, за которым она охотится. Если волчица и кролик оказываются в одном квадрате, волчица съедает кролика и по­лучает одно очко. В противном случае она теряет 0,1 очка.

Волки и волчицы с нулевым количеством очков умирают. В начальный момент времени все волки и волчицы имеют 1 очко. Волк ведет себя подобно волчице до тех пор, пока в соседних квадратах не исчезнут все кролики; тогда, если волчица находится в одном из восьми близлежащих квадратов, волк гонится за пей.Если волк и волчица окажутся в одном квадрате и там пег кролика, которого можно съесть, они производят потомство случайного пола.

Пронаблюдать за изменением популяции в течение некоторого периода времени. Проследить, как сказываются на эволюции популяций изменения параметров модели.

23.Промоделировать процесс распространения инфекции стригущего лишая по участку кожи размером n*n (п —нечетное) клеток.