лекции 8-14 / 14_Lec_9_10

9. Плоская монохроматическая волна

Уравнения Максвелла для монохроматического поля

iωµ(ω)H = c rot E, iωε(ω)E = −c rot H.

(9.12)

Среду считаем однородной (ε и µ не зависят от координат). Тогда, исключив из этих уравнений H, получим волновое уравнение

	∆E +	ω2	εµE = 0.	(9.13)
		c2

Напомним, что в случае вакуума мы рассматривали аналогичное волновое уравнение, в котором, однако, было εµ =1. Главное отличие рассматриваемого

случая – возможность комплексных ε . В средах с поглощением волновой вектор k должен быть комплексным

k = k′+ik′′.

Для плоской волны E, H ~ exp(ikr) , и уравнения Максвелла (12) сводятся к алгебраическим

ωµH = c[k ×E],				ωεE = −c[k ×H].					(9.14)
Исключив из них, например, H, найдем
k	2	= (k,k) = k	′2	−k	′′2	′	′′	ω2	(9.15)
						+ 2i(k ,k	) =	c2 εµ.

Как уже указывалось ранее (см. обсуждение после формулы (2.17)), даже при εµ =1 возможны комплексные волновые вектора, если только вещественные

вектора k′ и k′′ ортогональны друг другу, (k′,k′′) = 0 . При комплексных

волновых векторах мы имеем дело с неоднородными плоскими волнами. Для них плоскости постоянной амплитуды и фазы могут различаться. Из (14) следует

(k,E) = 0, (k,H) = 0, εE2 = µH2 .

(9.16)

Поскольку все вектора в этом соотношении комплексны, оно не имеет прежнего геометрического смысла.

Впрозрачной (непоглощающей) среде для однородной плоской волны k = ωc 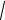εµ = ωc n,

где n = εµ - показатель преломления. Соотношения между E и H ( оба вектора ортогональны k в силу (16), так что волна поперечна)

	H =		ε		[l ×E],	l = k	,	ε | E |2 = µ | H |2 .	(9.17)
			µ
						k

При этом средняя за период плотность электромагнитной энергии (8.13) представляется в виде

	<U >=	1	d(ω2εµ)	| E |2 =	c		ε			dk	| E |2 .
		16πµω	dω		8π µ dω

Среднее значение плотности потока (модуль вектора Пойнтинга)

< S >= 8cπ 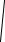µε | E |2 .

(9.18)

(9.19)

В поглощающей среде (комплексный вектор k) возможен случай, когда k′ и k′′ параллельны. Тогда плоская волна однородна, и можно ввести l - единичный вектор в общем направлении k′ и k′′, так что

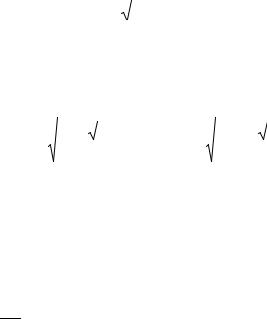
k = kl,

k =

ω

=

ω (n +iκ).

(9.20)

εµ

c

c

Здесь n -

показатель преломления, κ -

коэффициент поглощения среды. При

µ =1 связь n и κ с ε′ и ε′′ следующая (ε′′ > 0 для поглощающей среды)

(n

+iκ)

2

= ε

′

′′

+iε ,

откуда

ε′+

−ε′+

n =

ε′2

+ε′′2

κ =

ε

′2 +ε′′2

(9.21)

2

,

2

.

Еще одна интересная особенность плоских волн даже в прозрачных средах (с пренебрежимо малым поглощением) связана с принципиальной возможностью сред с одновременно отрицательными значениями диэлектрической и магнитной проницаемостей [обзор В.Г.Веселаго. УФН, 1967, том 92, № 3, стр. 517-526]. Более точно, прозрачные среды можно разделить на правые (ε > 0, µ > 0 ) и левые (ε < 0 , µ < 0 ). В правых средах вектора Е, Н и k

образуют правую тройку, и направление потока энергии (вектора Пойнтинга) S = 4cπ [E ×H] совпадает с направлением волнового вектора k. А в левых средах

направление S противоположное. Это приводит к существенным изменениям в эффекте Допплера, эффекте Вавилова-Черенкова, преломления плоской волны на границе раздела сред, замене светового давления на притяжение и т.д. Среди естественных оптических сред «левых» пока не обнаружено. Однако в определенной степени аналогичные композитные среды были созданы искусственно и в настоящее время интенсивно исследуются в радиодиапазоне.

Распространение импульсов излучения в среде с частотной дисперсией

Для однородной изотропной среды исходным служит вытекающее из

уравнений

~

;

знак

~ над

Максвелла волновое уравнение (µ =1, div E = 0

величиной

означает, что эта величина меняется

со временем с

высокой

(оптической) частотой)

~

1 ∂

2

~

D

∆E −

∂t 2

= 0.

(9.1)

c2

~

~

Для плоских волн с фиксированной поляризацией E

= E(z,t)e и

∂

2 ~

1

∂

2

~

E

−

D

= 0.

(9.2)

∂z2

c2

∂t 2

При этом

~

~

∫Eω (z)exp(−iωt)dω,

(9.3)

E(z,t) =

D(z,t) =∫ε(ω)Eω (z)exp(−iωt)dω.

В силу линейности задачи распостранение импульса излучения можно анализировать, разложив поле в спектр монохроматических волн. Амплитуды этих волн определятся начальным условием. А структуру самих волн мы уже рассмотрели. При этом возникает следующая особенность. Так как ε(ω) →1

при ω → ∞, то у компонент начального импульса, отвечающих весьма высоким частотам (по сравнению с резонансными частотами среды), скорость распространения в среде – та же, что в вакууме. Это – так называемый предвестник; отвечающая ему энергия для плавных сигналов весьма мала, но он, естественно, распространяется с наибольшей скоростью. Основная же по энергии часть импульса распространяется с меньшей скоростью, определяемой свойствами среды. Описанием этой части импульса квазимонохроматического

излучения мы и займемся в приближении квазиоптического уравнения. Для этого используем квазиоптическое уравнение

~

ω

(9.4)

k0

=

ε

(ω0 ).

E = Re{E(z,t)exp[i(k0 z −ω0t)]},

c

k 2 (ω) в

Разложим

функцию

ряд Тейлора около центральной частоты ω0 ,

ограничившись выписанными членами

k 2 (ω) ≈ k 2 (ω0 ) + 2k0

dk

(ω −ω0 ) +

1 d 2k 2

(ω −ω0 )2 .

(9.5)

dω

2 dω2

ω0

ω

~

0

1

∂

2

2

1

∂E

∂

2

Тогда

D

E

+ 2ik

− D

E

exp[i(k

z −ω

t)] ,

c2 ∂t 2

0

0

v

g

∂t

2

∂t 2

0

0

где введены групповая скорость vg и параметр квадратичной дисперсии D2

1

=

dk

,

D2 =

1 d 2k 2

.

(9.6)

vg

dω

ω

2 dω2

0

ω0

Объединяя эти результаты, приходим к следующему квазиоптическому уравнению для огибающей

∂E

1 ∂E

∂2 E

2ik

0

+

− D

2

2

= 0.

(9.7)

∂z

∂t

vg ∂t

Выписанное уравнение отвечает второму приближению по дисперсии (в

	разложении	(5) сохранялись квадратичные члены). В					первом приближении
	( D2 = 0 ) получаем уравнение переноса
	∂E +	1		∂E = 0.			(9.8)
		vg
	∂z			∂t
	Его общее решение
					z
	E = f		t −				(9.9)
					vg

где f - произвольная функция, она определяется начальным условием, например, при z = 0 : f (t) = E(0,t) . Это решение отвечает переносу без искажений

огибающей импульса с постоянной скоростью vg - групповой скоростью. Учет члена с D2 ≠ 0 позволяет описать искажения формы импульса. Для этого

удобнее перейти в бегущую с групповой скоростью систему координат, то есть заменить в (7) переменные

	(z,t) → (z,τ), τ = t −							z	.
	Тогда получим							vg
	2ik	0	∂E	− D	2	∂2 E	= 0.	(9.10)
			∂z			∂τ 2

Это уравнение того же типа, что дифракционное (4.7) при одномерной геометрии. Соответственно, его решение, выражающее временной профиль огибающей импульса в среде с координатой z через профиль входного сигнала (при z = 0)

						ik0
	i			′			′	2		′
E(z,τ) =	λD2 z ∫			E(0,t )exp −		λD2 z	(τ −t )		dt .		(9.11)

10. Электромагнитные волны в анизотропных средах

По природе анизотропия может быть естественной (кристаллы) или наведенной в исходно изотропной среде внешним электрическим или магнитным полем, деформацией тела и т.д. Материальные уравнения для монохроматического излучения

3	3
Di = ∑εij (ω)E j ,	Bi = ∑µij (ω)H j .	(10.1)
j=1	j=1

Обобщение на случай анизотропных сред выражения (8.6) для диссипации энергии в монохроматическом электромагнитном поле (за 1 сек в 1 см3) имеет вид

		iω	3
	Q =		∑{(εij −ε ji )Ei E j + (µij − µji )Hi H j	}.
	16π i, j=1
	Условие отсутствия поглощения
	εij = ε ji ,		µij = µji .

(10.2)

(10.3)

В отсутствие воздействия на среду внешнего магнитного поля тензоры εij и µij симметричны

εij = ε ji , µij = µji .	(10.4)
Тогда условие (3) сводится к требованию вещественности εij	и µij . Для

непоглощающих сред плотность внутренней энергии электромагнитного поля (обобщение формулы (8.13))

3

∂(ωε

′ )

∂(ωµ′ )

1

∑

ij

ij

(10.5)

U =

Ei E j

∂ω

+

∂ω

Hi H j .

16π i, j=1

ω

0

ω

0

Плоская монохроматическая волна в анизотропной среде

Считаем, что среда немагнитная (µ =1) и прозрачная (εij′′ = 0 ) (в

рассматриваемой области частот). Тогда уравнения Максвелла для монохроматической волны

iωH = c rot E, iωD = −c rot H.

(10.6)

Для плоской волны E, H ~ exp(ikr), k - вещественный волновой вектор. Для такой волны (6) преобразуется к алгебраическим соотношениям

ω H =[k ×E],						ω D = −[k ×H].	(10.7)
c						c
Исключив отсюда H и используя материальное уравнение D = εˆE , запишем
дисперсионное соотношение в виде
[k ×[k ×E]] +				ω2			(10.8)
					c2	εˆE = 0.
Согласно (7),	три вектора k, D и H взаимно перпендикулярны (см. рис.);
H E, E, D,k		лежат в одной плоскости. В той же плоскости лежит и вектор
Пойнтинга S =		c	[E ×H]. Введем безразмерный вектор n, направленный вдоль
		4π
волнового вектора k
k = ω n.							(10.9)
c

В изотропной среде n = 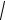ε(ω) = n(ω) - показатель преломления. Соотношения

(7) переписываются в виде

H =[n ×E],	D = −[n ×H].	(10.10)
Отсюда
D =[n ×[E ×n]] = n2E −n(n,E).		(10.11)
По компонентам, используя материальные уравнения (1),
3	3
n2 Ei − ni ∑n j E j = ∑εij E j
j=1	j=1
или
3
∑(n2δij − ni n j −εij )E j = 0.		(10.12)
j=1
Условие совместности однородной системы (12)
Det (n2δij − ni n j −εij ) = 0.		(10.13)

Вещественный симметричный тензор εij всегда может быть приведен к диагональному виду

	ε	( x)	0		0
		0
εˆ =			ε( y)		0	.
		0	0	ε	( z)

В соответствующей системе координат, отвечающей главным осям кристалла, уравнение (13) примет вид

n2 (ε(x) nx2 +ε( y) n2y +ε(z) nz2 ) −

−[nx2ε(x) (ε( y) +ε(z) ) + n2yε( y) (ε(x) +ε(z) ) + nz2ε(z) (ε(x) +ε( y) )] +ε(x)ε( y)ε(z) = 0.

(10.14)

Это – уравнение Френеля. При заданных частоте ω , осях и главных значениях тензора εij , а также направлении волнового вектора плоской волны k/k это

квадратное уравнение для n2 с вещественными коэффициентами. Соответственно, два решения квадратного уравнения отвечают двум различным абсолютным значениям волнового вектора для линейно поляризованных волн с ортогональными поляризациями.

		c	Направление потока энергии задается вектором Пойнтинга S,
	S =		[E ×H], S E, H . Обычно вместо S вводится так называемый лучевой
		4π

вектор s, направление которого совпадает с направлением S, а величина определяется соотношением

(s,n) =1.		(10.15)
Соответственно,
(s,E) = 0,	(s, H) = 0.	(10.16)
Умножаем уравнения (10) векторно на s. Тогда с учетом (16)
[s ×D] = H,	[s ×H] = −E.	(10.17)

Сравним эту систему уравнений с (10). Они переходят друг в друга при замене

n ↔ s, D ↔ E, εˆ ↔ηˆ.

(10.18)

Последняя замена относится и к материальному уравнению D = εˆE , которое следует заменить на следующее E =ηˆD , где ηˆ = εˆ−1 - тензор, обратный тензору εˆ . Поэтому при замене (18) волновое уравнение Френеля (13) переходит в

Det (s2δij − si s j −ηij ) = 0.

(10.19)

Это уравнение лучевой поверхности, которое, вообще говоря, эквивалентно уравнению Френеля. Оно также существенно, поскольку лучевой вектор s определяет направление потока энергии, направление групповой скорости волн и направление распространения пучков. Первое из этих утверждений очевидно.

Покажем второе. По определению групповой скорости v g = dω / dk . Выделим направление вектора E (e - единичный вектор): E(r) = E(r)e. Тогда

S =

c

E 2 (r)[e

×[k

×e]].

(10.20)

4π

Подставим это выражение в волновое уравнение (8)

[k ×[k ×e]] +

ω

2

εˆe

= k(k,e) −(k,k)e

+

ω2

εˆe =

0.

(10.21)

c2

c2

Умножаем (21) скалярно на e

(k,k) −(k,e)2 −

ω2

eεˆe = 0.

(10.22)

c2

Дифференцируем (22) по k

ω

eεˆe +

ω2

dεˆ

dω

2k − 2(k,e)e −

2

e

e

= 0.

2

2

c

c

dω

dk

Отсюда

k −(k,e)e

[e ×[k ×e]]

vg = dω

=

=

.

ω

ω2

dεˆ

ω

ω2

dεˆ

dk

eεˆe +

e

e

eεˆe +

e

e

c2

2c2

dω

c2

2c2

dω

С учетом (20) получаем, что направления групповой скорости vg и лучевого вектора s (или же вектора Пойнтинга S) совпадают. О направлении распространения пучка см. [Виноградова, Руденко, Сухоруков].

Если направление волнового вектора варьируется, то уравнение Френеля (14) определяет в координатах nx , ny , nz поверхность волновых векторов. Эта

поверхность может быть трех типов.

I. Кубические кристаллы (ε( x) = ε( y) = ε( z) ) . Уравнение Френеля принимает вид

(n2			−ε( z) )2			= 0.			(10.23)
Поверхность волновых векторов –								сфера nx2 + ny2 + nz2 = ε( z) . В	оптическом
отношении среда изотропна.								ε( x) = ε( y) = ε , ε( z) = ε|| , ε ≠ ε|| . Ось z -
II. Одноосные кристаллы. Например,
оптическая ось кристалла. Уравнение Френеля
(n2			−ε )[ε||nz2 +ε (nx2 + ny2 ) −ε ε|| ] = 0.						(10.24)
или
n2			= ε ,						(10.25)
	n2			nx2	+ ny2				(10.26)
	z		+				=1.
	ε				ε||

В этом случае поверхность волновых векторов распадается на две раздельные поверхности – сферу (25) и эллипсоид вращения (26). Для обыкновенной волны (25) показатель преломления не зависит от направления волнового вектора (как в изотропной среде или одноосном кристалле). В этом случае направления волнового и лучевого векторов и, соответственно, направления фазовой и

групповой скоростей совпадают. Для необыкновенных волн (26) модуль волнового вектора (показатель преломления n для волны с соответствующим направлением распространения) зависит от угла θ между волновым вектором k

и осью z (nz = n cosθ, nx2 + ny2 = n2 sin2 θ)

1	=	sin 2	θ	+	cos2	θ	.	(10.26)
n2		ε||			ε

Поляризации обыкновенных и необыкновенных волн линейные и взаимно ортогональные.

III. Двуосные кристаллы. В этом случае все три значения	ε( x) , ε( y)	и ε( z)
различны. Считаем ε( x) < ε( y) < ε( z) . Исследуем уравнение	Френеля.	Найдем

форму сечений поверхности волновых векторов координатными плоскостями.

nz = 0 : (n2 −ε( z) )(ε( x) nx2 +ε( y) ny2 −ε( x)ε( y) ) = 0,

nx2 + ny2 = ε( z) ,		n2		ny2		(10.27)
		x	+			=1,
		ε( y)		ε( x)
ny = 0 : (n2 −ε( y) )(ε( x) nx2 +ε( z) nz2 −ε( x)ε( z) ) = 0,
	2			2		(10.28)
nx2 + nz2 = ε( y) ,		nx	+	nz		=1,
		ε( z)		ε( x)
nx = 0 : (n2 −ε( x) )(ε( y) ny2 +ε( z) nz2 −ε( y)ε( z) ) = 0,
ny2 + nz2 = ε( x) ,		ny2		n2		(10.29)
			+	z			=1.
		ε( z)		ε( y)
Как видно из (27)-(29), эти сечения являются окружностями или
эллипсами. В плоскостях	nx = 0			и	nz = 0 соответствующие окружности и
эллипсы не пересекаются.	Более интересно сечение, отвечающее ny = 0 (см.

рис.). Пересечение описываемых нижней строкой (28) уравнений окружности и эллипса приводит к соотношениям

nx2 =	ε( z) (ε( y) −ε( x) )	,	nz2 =	ε( x) (ε( z) −ε( y) ) .	(10.30)
	ε( z) −ε( x)			ε( z) −ε( x)

В соответствии с (30), имеется 4 точки пересечения (± nx , ± nz , особые

точки, или точки самопересечения поверхности). Через противоположные точки проходят прямые, называемые оптическими осями, или бинормалями кристалла. Эти направления – единственные, вдоль которых волновой вектор имеет только одно значение. Для остальных направлений таких значений два.

Аналогичны свойства лучевой поверхности (замена n ↔ s, εˆ ↔ηˆ ). Отвечающие самопересечению этой поверхности бирадиали также расположены в плоскости ny = 0.

Соотношение между векторами n и s в общем случае однозначное. Исключением служат направления n вдоль бинормали (внутренняя коническая рефракция) и вектора s вдоль бирадиали (внешняя коническая рефракция).При этом одному, например, волновому вектору (n) отвечает целый конус лучей s (внутренняя коническая рефракция, см. рис., кристалл вырезан перпендикудярно бинормали).

При малых отклонениях направления от бинормали или бирадиали вырождение снимается. Поскольку пучок состоит из набора плоских волн (или

лучей), это обстоятельство приводит к тонкой структуре явления конической рефракции [Борн, Вольф].