лекции 8-14 / Lec_11

11. Двойное преломление в постоянном электрическом поле

При наложении постоянного электрического поля напряженности E(s) исходно изотропная среда становится анизотропной. Строго говоря, это уже предмет нелинейной электродинамики, поскольку свойства среды меняются под действием электрического поля. При малых напряженностях поля удобно описание с разложением диэлектрического тензора в ряд по степеням электрической напряженности E(s). Например, для кристаллов определенной симметрии существует уже линейный эффект

εij = εij(0) + ∑3	αijm Em(s) .	(11.1)
m=1

Здесь αijm - тензор третьего ранга. Если исходная среда изотропна

(εij(0) = ε(0)δij ) , то αijm = 0 , и низшим служит квадратичный по E(s) член (α - скаляр)

εij = ε(0)δij +αEi(s) E(js) .

(11.2)

Такая среда эквивалентна одноосному кристаллу (эффект Керра). Одна из главных осей тензора совпадает с направлением (статического) электрического поля, и соответствующее главное значение

ε|| = ε(0) +αE(s)2 .	(11.3)
Два остальные главные значения равны друг другу	ε = ε(0) , и

соответствующие главные оси лежат в плоскости, перпендикулярной полю E(s).

Магнитооптические эффекты

Аналогично, анизотропия возникает и при включении постоянного магнитного поля напряженности H(s). Однако, ее характер другой. Так, для прозрачной

(непоглощающей) среды тензор εij может быть комплексным, причем требование его симметрии заменяется условием эрмитовости (см. (10.3))

εij = ε ji ,

(11.4)

что означает

εij′ = ε′ji , εij′′ = −ε′ji′.

(11.5)

При учете общего соотношения

εij (H(s) ) = ε ji (−H(s) )

(11.6)

находим

εij′ (H(s) ) = ε′ji (H(s) ) = εij′ (−H(s) ), εij′′(H(s) ) = −ε′ji′ (H(s) ) = −εij′′(−H(s) ).	(11.7)
Введем также обратный тензор
ηij = εij−1 =ηij′ +iηij′′.	(11.8)

Антисимметричный тензор второго ранга ηij′′ имеет только 3 независимые

компоненты и эквивалентен одному (аксиальному) вектору, который обозначим как G - вектор оптической активности

ηij′′ = ∑3 eijmGm ,	(11.9)
m=1

или в компонентах

η′xy′ = Gz , η′zx′ = Gy , η′yz′ = Gx .

(11.10)

В (9) введен eijm - единичный антисимметричный тензор, e123 =1, остальные

элементы – либо нули (при совпадении хотя бы двух индексов), либо ±1, в зависимости от типа перестановки индексов. Теперь

Ei = ∑3	(ηij′ +ieijmGm )Dj =∑3	ηij′Dj +i[D×G]i .	(11.11)
j=1	j=1

Аналогично

Di	= ∑3		εij E j		+i[E ×g]i ,	(11.12)
	j=1
где g - вектор гирации,
Gi	= −		1	∑3	εij′g j , | ε |= Detεij .	(11.13)
		| ε | j=1

Рассмотрим теперь вызванные слабым внешним магнитным полем эффекты анизотропии в исходно изотропной среде. Связь D и E при малых H(s)

	E =	1	D +i[D×G], D = ε(0) E +i[E ×g],		(11.14)
		ε(0)
	где ε(0) -	диэлектрическая проницаемость исходной изотропной среды в
	отсутствие	магнитного поля. При этом G = −		1	g, g = fH(s) , скалярная
				ε(0)2

постоянная f может быть любого знака. Поверхность волновых векторов (уравнение Френеля) описывается уравнением

n±2 = n02 ± gz

(11.15)

(ось z выбрана вдоль n). Таким образом,при каждом направлении k (n) имеется два значения волнового числа. Эти два значения отличаются поляризациями волны

Dx = iDy ,

то есть имеются две круговые поляризации с противоположным направлением вращения.

Если исходное излучение линейно поляризовано, то его можно разложить на две волны с противоположными круговыми поляризациями, которые будут распространятся с различными волновыми векторами

k± = ωc n± .Тогда после прохождения слоя среды толщины l волна останется линейно поляризованной, но плоскость поляризации повернется на угол

ωgl	cosθ,	(11.16)
2cn0

где θ - угол между n и g (эффект Фарадея). При учете квадратичных по H(s) членов возникают и другие эффекты. В том числе при n g эффект Фарадея

отсутсутствует, а имеется эффект Коттона-Мутона – излучение с исходной линейной поляризацией после прохождения слоя среды становится эллиптически поляризованным.

Для пьезоэлектриков материальное уравнение включает тензор механических напряжений σ :

Di = Di(0) +εik Ek +γi,klσkl .

При этом к уравнениям Максвелла следует добавить уравнения механики сплошной среды. Первый член в правой части этого уравнения может быть отличен от нуля, то есть индукция может иметь ненулевое значение даже в отсутствие поля, в пироэлектриках (сегнетоэлектриках). Применительно к магнитным средам это ферромагнетики, где имеются домены намагниченности.

Пространственная дисперсия

При наличии не только частотной, но и пространственной дисперсии материальные уравнения, применительно к плоским монохроматическим волнам, имеют вид (7.11)-(7.13). Далее считаем среду немагнитной (µ =1).

Дисперсионное уравнение, связывающее ω и k, выводится так же, как и при описании только частотной дисперсии. Напомним, что для плоских

монохроматических волн с пространственно-временной	зависимостью
~ exp[i(kr −ωt)] дифференциальные уравнения Максвелла	сводятся к
алгебраическим

[k ×H] = −	ω D,	[k ×E] =	ω H, (k, D) = 0, (k, H) = 0.	(11.17)
	c		c

Исключим из этих уравнений H. Умножаем второе из этих уравнений слева векторно на k, используем соотношение векторной алгебры для двойного векторного произведения

	[k ×[k ×E] = k(k,E) −k 2E = −			ω2		D.	(11.18)
				c2
	С учетом (7.11) в тензорных обозначениях
	3		2
	∑[k 2δij	−ki k j −	ω2 εij (ω,k)]E j		= 0, i =1,2,3.		(11.19)
	j=1		c

Ненулевое решение этой ситемы возможно только при условии их совместности

	Det[k 2δij −ki k j −	ω2	εij (ω,k)] = 0 .	(11.20)
		c2

Как и ранее, удобно вместо k ввести безразмерный вектор n, k = ωc n ; тогда

Det[n2δij −ni n j −εij (ω,n)] = 0.

(11.21)

Это диперсионное уравнение служит обобщением уравнения (10.12) кристаллооптики.

Обычно в оптике эффекты пространственной дисперсии малы, определяясь малым параметром a/λ, где a - характерный для рассматриваемой

среды размер (атомные размеры, длина пробега в газах и т.д.) и λ - длина волны света. Это позволяет, не конкретизируя модели среды, получить приближенное описание эффектов пространственной дисперсии.

Учет соотношения a/λ << 1 позволяет использовать под интегралом

(7.13) разложение (R = x1ex + x2e y + x3ez )

			3	1	2
exp[−i(k,R)] = exp[−i	ω	(n, R)] =1−i	ω ∑nl xl −		ω2
	c		c l=1	2	c

Тогда (7.13) преобразуется к виду

∑3 nl nm xl xm +... (11.22)

l,m=1

εij (ω,k) =δij + 4π∞∫dτ exp(iωτ)∫dRκij (R,τ) −

0

−i4π ω	∑3 nl	∞∫dτ exp(iωτ)∫dRκij (R,τ) xl −
c	l=1	0
−2π ω22	∑3 nl nm ∞∫dτ exp(iωτ)∫dRκij (R,τ) xl xm +...
c	l,m=1	0
или
εij (ω,k) = εij (ω,k) −i∑3			γijl (ω)nl − ∑3	αijml (ω)nl nm +...
		l=1	l,m=1
Из сопоставления (23) с (24)

εij (ω) =δij + 4π∞∫dτ exp(iωτ)∫dRκij (R,τ),

0

(11.23)

(11.24)

γijl (ω) = 4π	ω ∞ dτ exp(iωτ)	∫	dRκij (R,τ) xl ,	(11.25)
	c ∫0

ω2 ∞

αijlm (ω) = 2π c2 ∫0 dτ exp(iωτ)∫dRκij (R,τ) xl xm .

Соотношение (24) является разложением исходного уравнения (7.13) в ряд по степеням a / λ <<1. Напомним, что функция κij – вещественная, а εij

может быть комплексной величиной, εij (ω,k) = εij′ (ω,k) +εij′′(ω,k) . В

пренебрежении поглощением все тензоры (25) вещественны. Для оптически неактивных (негиротропных) сред, состоящих из молекул или кристаллических ячеек с центром симметриии, в разложении (24) нет членов с нечетными степенями k (n), так что

εij (ω,k) = εij (ω,−k).

(11.26)

В противном случае среда (без центра симметрии) гиротропна, для нее

εij (ω,k) = ε ji (ω,−k).

(11.27)

В отсутствие поглощения при этом тензор εij (ω,k) эрмитов:

εij (ω,k) = εij (ω,−k).

Аналогичные выражения можно выписать для обратного тензора ηˆ = εˆ−1 :

	Ei (ω,k) = ∑3	ηij (ω,k)D(ω,k),
	j=1			(11.28)
	ηij (ω,k) =ηij (ω) +i∑3		gijl (ω)nl +∑3
				βijlm (ω)nl nm +...
		l=1	l,m=1

Далее считаем, что среда изотропна. Рассмотрим отдельно эффекты пространственной дисперсии для гиротропных и негиротропных сред.

Гиротропная среда

Поскольку пространственная дисперсия проявляется уже в членах ~ a / λ, ими и ограничимся. Ввиду изотропии среды

εij (ω) = ε(ω)δij ,

γijl (ω) =γ(ω)eijl ,

gijl (ω) = g(ω)eijl .

(11.29)

Здесь eijl -

единичный полностью антисимметричный тензор третьего ранга,

eijl = 0, ±1,

eijl

≠ 0

только при различии всех индексов, e123

=1, eijl

меняет знак

при перестановке любых двух индексов.

Теперь

εij (ω,k) = ε(ω)δij −iγ(ω)∑3 eijl nl ,

ηij (ω,k) =η(ω)δij +ig(ω)∑3 eijl nl .

(11.30)

l=1

l=1

При использовании (30) соотношение (19) принимает вид

3

2

2

3

∑{[k 2

−ω2

ε(ω)]δij −ki k j −i ω2 γ(ω)∑eijl nl }E j = 0.

(11.31)

j=1

c

c

l=1

Направим ось z вдоль k, тогда

n = nez , k = (ω / c)nez ,

и уравнения (31)

запишутся так:

i =1

[k 2

−

ω2

ε(ω)]Ex −i

ω2

γ(ω)nEy = 0,

c2

c2

i = 2

[k 2

−

ω2

ε(ω)]Ey

+i

ω

2

γ(ω)nEx = 0,

(11.32)

c2

c2

i = 3

[k 2

−

ω2

ε(ω)]Ez −k 2 Ez = 0.

c2

Из последнего уравнения следует,

что Ez

≠ 0 возможно только при ε(ω) = 0 .

При этом фазовая скорость равна нулю, то есть бегущих продольных волн нет. Для поперечных волн (Ez = 0 ) из двух оставшихся уравнений

[n2 −ε(ω)]2 −γ 2 (ω)n2 = 0.

(11.33)

Учитывая малость γ 2 << ε , найдем

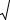
n2	= ε(ω) ±γ(ω)	ε(ω)	,	(11.34)
1,2

причем

	Ex	= ±i.	(11.35)
	Ey

Таким образом, в каждом направлении могут распространятся две поперечные нормальные волны с различными фазовыми скоростями. Волны обладают противоположными круговыми поляризациями. В этом случае также будет происходить поворот плоскости поляризации линейно-поляризованной волны (эффект Фарадея).