
- •Старооскольский технологический институт им. А.А. Угарова
- •Лабораторная работа №1 Шифрование данных методом замены в симметричных криптосистемах.
- •Теоретическое введение
- •Аффинная система подстановок Цезаря.
- •Задание на лабораторную работу
- •Лабораторная работа №2 Шифрование с использованием метода гаммирования и датчиков псевдослучайных чисел
- •Теоретическое введение
- •Задание на лабораторную работу
- •Лабораторная работа №3
- •Теоретическое введение
- •Порядок выполнения работы
- •Задание на лабораторную работу
- •Лабораторная работа №4 Шифрование данных в асимметричной криптосистеме rsa
- •Теоретическое введение
- •Задание на лабораторную работу
- •Лабораторная работа №5 Алгоритм электронной цифровой подписи rsa
- •Теоретическое введение
- •Задание на лабораторную работу
- •Лабораторная работа №6 Алгоритм Диффи-Хелмана для безопасного обмена ключами
- •Теоретическое введение
- •Задание на лабораторную работу
- •Список литературы
- •Приложение
Аффинная система подстановок Цезаря.
Символы алфавита Zm можно не только складывать по модулю m, но и умножать по этому модулю. Применяя одновременно операции сложения и умножения по модулю m над элементами множества Zm, можно получить систему подстановок, называемую аффинной системой подстановок Цезаря. Аффинная система – это одновременное сложение и умножение по mod m над элементами Zm.
Еa,b : Zm Zm
Еa,b : t Еa,b(t)
Еa,b(t) = (at + b)mod m;
a, b – целые числа, причем 0 < a, b < m: НОД(a, m) = 1.
Здесь буква, соответствующая t, заменяется на букву, соответствующую (at + b)mod m
такое преобразование взаимно однозначно в том и только в том случае, когда числа a и m являются взаимно простыми.
Например, пусть m = 33, a = 5, b = 3. Тогда наименьший общий делитель НОД(5, 33) = 1, и мы получаем следующее соответствие между числовыми кодами букв:
|
t |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
5t+3 |
3 |
8 |
13 |
18 |
23 |
28 |
33 |
5 |
10 |
15 |
20 |
|
t |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
|
5t+3 |
15 |
30 |
2 |
7 |
12 |
17 |
22 |
27 |
32 |
4 |
9 |
|
t |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
32 |
|
5t+3 |
14 |
19 |
24 |
29 |
1 |
6 |
11 |
16 |
21 |
26 |
31 |
Преобразуя числа в буквы русского алфавита, получаем следующее соответствие для букв открытого текста и шифртекста:
|
А |
Б |
В |
Г |
Д |
Е |
Ж |
З |
И |
Й |
К |
Л |
М |
Н |
О |
П |
Р |
|
Г |
И |
Н |
Т |
Ч |
Ъ |
_ |
Е |
К |
П |
Ф |
П |
Ю |
В |
З |
М |
С |
|
С |
Т |
У |
Ф |
Х |
Ц |
Ч |
Ш |
Щ |
Ь |
Ы |
Ъ |
Э |
Ю |
Я |
_ |
|
|
Ц |
Ы |
_ |
Д |
Й |
О |
У |
Ш |
Э |
А |
Ж |
Л |
Р |
Х |
Ь |
Я |
|
Исходное сообщение:
МОСКОВСКИЙ_ИНСТИТУТ_СТАЛИ_И_СПЛАВОВ,
будет выглядеть следующим образом:
ЮЗЦФЗНЦФКПЯКВЦЫКЫ_ЫЯЦЫГПКЯКЯЦМПГНЗН.
Здесь ключ – это пара чисел a, b.
Криптосистема Хилла.
Алгебраический метод, обобщающий аффинную подстановку Цезаря
Еa,b : Zm Zm,
Ea,b(t) = t at + b(mod m)
для определения n-грамм, был сформулирован Лестером С. Хиллом.
Множество целых Zm, для которого определены операции сложения, вычитания и умножения по модулю m, является примером кольца. Кольцо R представляет собой алгебраическую систему в которой определены операции сложения, вычитания и умножения пар элементов. Эта алгебраическая система обладает рядом свойств:
элементы кольца R образуют коммутативную группу относительно операции сложения; кроме того, существуют единичный и обратный элементы относительно операции сложения,
умножение и сложение удовлетворяют ассоциативному и дистрибутивному законам.
Мультипликативное обратное -1 элемента кольца может существовать не всегда. Например, если модуль m = 26, то значения 2-1(mod 26) и 13-1(mod 26) не могут существовать.
Если модуль m является простым числом р, то существует обратная величина любого ненулевого элемента t из Zp (при m = р), поскольку значения
t (mod m), 2t (mod m), 3t (mod m), .... ,(p-1) t (mod m)
различаются, если 1 t p -1.
Множество Zp, где р – простое число, является примером алгебраической системы, называемой конечным полем. Ненулевые элементы Zp образуют мультипликативную группу.
Множество всех n-грамм х = (х0, х,, х2,.... xn-1) с компонентами из кольца Zm образует векторное пространство Zm,n над кольцом Zm. Каждая n-грамма х называется вектором. В векторном пространстве Zmn для векторов х определены операции сложения и вычитания по модулю n, а также скалярное умножение вектора на элемент t кольца Zm . Сложение и скалярное умножение являются операциями, удовлетворяющими коммутативному, ассоциативному и дистрибутивному законам. Вектор х является линейной комбинацией векторов
{х(i): 0 <i < L}, если
х = t0x(0) + t1x(1) +... + tL-1.,x(L-1)(mod m).
Линейное преобразование Т является отображением:
T : Zm,n Zm,n,, T : x y, y=T(x),
которое удовлетворяет условию линейности
T = (tx + sy)-tТ(х) + sТ(у) (mod m) для всех s, t в Zm и х, у в Zm п.
Линейное преобразование Т может быть представлено матрицей размером nn вида
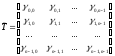
причем .
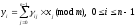
Базисом
для векторного пространства
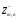 является
наборвекторов
из {х(i)
: 0 < i
< L},
которые линейно независимы и порождают
является
наборвекторов
из {х(i)
: 0 < i
< L},
которые линейно независимы и порождают
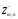 .Каждый
базис для
.Каждый
базис для содержитn
линейно независимых
векторов Любой набор из n
векторов, которые линейно независимы
над
содержитn
линейно независимых
векторов Любой набор из n
векторов, которые линейно независимы
над
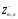 является
базисом.
является
базисом.
Пусть
 является линейным преобразованием,
описываемымматрицей,
причем
является линейным преобразованием,
описываемымматрицей,
причем
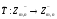 .
.
Если
векторы {х(i)
0 < i
< n}
линейно независимы над
 ,
тогда
их образы {Т(х(i))
: 0
i
< п}
линейно независимы над
,
тогда
их образы {Т(х(i))
: 0
i
< п}
линейно независимы над
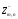 только в том случае, если определитель
матрицы
только в том случае, если определитель
матрицы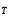 ,
обозначаемый как det
(Т),
не делится на любое простое р,
которое делит m.
В этом случае
преобразование
,
обозначаемый как det
(Т),
не делится на любое простое р,
которое делит m.
В этом случае
преобразование
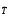 называется обратимым (или невырожденным)
линейным преобразованием, имеющим
обратное преобразование
называется обратимым (или невырожденным)
линейным преобразованием, имеющим
обратное преобразование
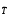 ,
где l-единичная
матрица. Кроме того,
,
где l-единичная
матрица. Кроме того,
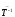 также является линейным
преобразованием.
также является линейным
преобразованием.
Например, когда m = 26 и матрица преобразования
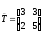
 ,
,
то определитель этой матрицы
det(T) = 9 = 1(mod 2),
det(T) = 9 = 9{mod 13).
Поэтому
существует обратное преобразование
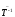 .
Нетрудноубедиться,
что
.
Нетрудноубедиться,
что

удовлетворяет
соотношению
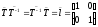 .
.
Пусть
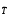 является линейным преобразованием на
является линейным преобразованием на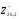 сматрицей
сматрицей
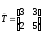
Используем
это преобразование
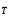 для определения биграммной
подстановки в английском алфавите
{ABCDEFGH..XYZ}.
Сначала
разобьем n-грамму
открытого текста на биграммы, причем
выберем
n
кратным 2. Например, 12-грамма PAYMOREMONEY
делится
на шесть биграмм:
для определения биграммной
подстановки в английском алфавите
{ABCDEFGH..XYZ}.
Сначала
разобьем n-грамму
открытого текста на биграммы, причем
выберем
n
кратным 2. Например, 12-грамма PAYMOREMONEY
делится
на шесть биграмм:
PA YM OR EM ON EY
Затем в каждой биграмме открытого текста заменим каждую букву ее числовым эквивалентом из таблицы:
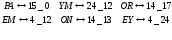 .
.
Преобразование
биграмм
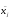 открытого текста в биграммы
открытого текста в биграммы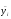 ,шифртекста
осуществляется в соответствии с
уравнением
,шифртекста
осуществляется в соответствии с
уравнением
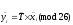

или
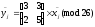
где
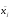 и
и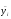 –
вектор столбцов биграмм шифртекста и
открытого текста соответственно.
–
вектор столбцов биграмм шифртекста и
открытого текста соответственно.
Получаем
 ,
,
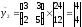
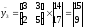
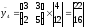

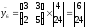 .
.
Заменяя в биграммах шифртекста числа на соответствующие буквы согласно таблицы, получаем 12-грамму шифртекста
ТЕ ЕЕ PJ WQ DP GY
Для расшифрования
биграмм
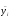 ,
шифртекста и восстановления биграмм
,
шифртекста и восстановления биграмм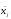 открытого
текста необходимо выполнить обратное
преобразование
открытого
текста необходимо выполнить обратное
преобразование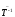 согласно
уравнению
согласно
уравнению
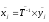
В рассмотренном примере матрицы преобразования имели размер 2x2 и шифровались биграммы (пары) букв Хотя буква Е может быть зашифрована по-разному в различных парах исходного сообщения одна и та же пара, например ЕМ будет шифроваться всегда одинаково на протяжении всего исходного текста.
