Лабораторные ТПР 5 лаба "Б"

Федеральное агентство по образованию

Модели и методы принятия решений

Лабораторный практикум для вузов

Составители: Т.М. Леденева, Т.Н. Недикова, М.Ю. Тафинцева

Воронеж 2006

2

Утверждено Научно-методическим советом факультета прикладной математики, информатики и механики ВГУ, протокол № 3 от 21.11.2006.

Рецензент к.ф.-м.н., доцент Т.В. Азарнова

Лабораторный практикум подготовлен на кафедре программного обеспечения и администрирования информационных систем Воронежского государственного университета.

Рекомендовано для студентов 4–5 курсов дневного отделения, изучающих следующие дисциплины: «Модели и методы принятия решений», «Методы экспертных оценок».

Для специальностей: 010503 (351500) – Математическое обеспечение и администрирование информационных систем и 010502 (351400) – Прикладная информатика в юриспруденции.

3

Лабораторная работа № 1

ПРИНЯТИЕ РЕШЕНИЙ В УСЛОВИЯХ РИСКА

Цель – ознакомить с классическими и производными критериями принятия решений в условиях риска.

Теоретический минимум

Проблема принятия решений в условиях риска возникает в том случае, когда с каждой принимаемой стратегией xi связано множество воз-

можных результатов {r1 ,r2 ,...,rm}, каждый из которых происходит с вероятностью p( rj / xi ). Исходная информация задается в виде таблицы (табл. 1),

строки которой соответствуют стратегиям

xi (i =

), а столбцы – вари-

1,n

антам возможных результатов rj (j =

). Элемент uij

представляет со-

1,m

бой числовую

оценку

предпочтительности (ценность, полезность)

uij = u (xi ,rj ) результата rj

при использовании стратегии xi .

Таблица 1.

rj

r1

r2

...

rm

xi

x1

u11

u12

u1m

x2

u21

u22

u2m

...

xn

un1

un2

unm

Пусть заданы условные вероятности p( rj / xi ), тогда для каждой стра-

тегии можно определить ожидаемую полезность в виде математического ожидания

m

E( xi ) = ∑u( rj ,xi )p( rj / xi ), i =1,n .

j=1

Решающее правило для определения оптимальной стратегии выглядит следующим образом:

xопт = arg max (E (xi )).

Одним из определяющих факторов принятия решений в условиях риска является внешняя среда. Поэтому в другой интерпретации xi – аль-

тернативы, rj – варианты внешних условий (среды), uij = u (xi ,rj ) – оценка предпочтительности альтернативы xi при условии, что наступило состояние среды rj . Введем необходимые обозначения: пусть внешняя среда может находиться в одном из состояний S1 ,S2 ,...,Sp , {x1 ,x2 ,...,xn} – множество возможных вариантов решения, каждому варианту xi вследствие различ-

4

ных внешних условий S j могут соответствовать различные оценки uij ре-

шений. Исходная информация также может быть представлена табл. 1, но rj соответствует S j .

Задача выбора оптимального решения в условиях риска опирается на различные критерии выбора. Рассмотрим основные критерии.

Максминный критерий

Fmax−min = max minuij

i j

означает, что выбранные в соответствии с ним варианты решения полностью исключают риск. ЛПР не может столкнуться с худшим результатом, чем тот, на который он ориентируется, т.е. данный критерий соответствует максимальной осторожности ЛПР и отражает идею получения гарантированного результата.

Минмаксный критерий

Fmin−max = mini maxj uij

также соответствует принципу гарантированного результата, но в том случае, если, например, uij – это оценка риска.

Максмаксный критерий (критерий азартного игрока)

Fmax−max = max maxuij ,

i j

или критерий крайнего оптимизма, соответствует явно расположенному к риску ЛПР.

Критерий Байеса-Лапласа (BL-критерий)

FBL = max ∑p		uij qj ,
i	j=1

где qj – вероятность появления внешнего состояния S j . Позиция приме-

няющего критерий Байеса-Лапласа оптимистичнее, чем в случае минмаксного критерия, однако, она предполагает более высокий уровень информированности.

Критерий Сэвиджа

FS =minmaxi j (maxui ij −uij ),

где величина maxuij −uij = aij определяет максимальный дополнительный

i

выигрыш, который достигается, если в состоянии S j вместо варианта xi

выбрать другой, оптимальный для этого состояния вариант. Однако можно интерпретировать aij и как потери (штрафы), возникающие в состоянии S j

при замене оптимального для него варианта на вариант xi . Тогда величина

max aij представляет собой максимальные возможные потери при выборе

j

варианта xi . Критерий Сэвиджа в этом случае иначе называют критерием минимального сожаления, где сожаление для i-й альтернативы при j-м со-

5

стоянии среды определяется в виде aij = max uij −uij . Критерий Сэвиджа

i

используется в той же ситуации принятия решений, что и минмаксный критерий.

Перечисленные критерии называются классическими. Ими предъявляются достаточно жесткие требования к анализируемой ситуации, поэтому они применимы только для идеализированных практических решений. Причем целесообразно применять поочередно несколько подходящих критериев, после чего из полученных вариантов ЛПР волевым образом определяет окончательное оптимальное решение. Такой подход позволяет, вопервых, лучше проникнуть во все внутренние связи проблемы принятия решений и, во-вторых, ослабляет влияние субъективного фактора.

Рассмотрим производные критерии.

Критерий Гурвица (H-критерий)

FH = maxi {c minuj ij +(1 −c )maxuj ij },

где c – весовой коэффициент. При c =1 критерий Гурвица превращается в минимаксный критерий; при c =0 – в критерий азартного игрока. Чаще всего используется с =0.5 , как «средняя точка» между оптимизмом и пессимизмом.

Критерий Ходжа-Лемана (HL-критерий)

				FHL		p			,
					= max c∑uij qj +(1 −c )minuij
		[	]		i	j=1	j
	где c				степень	доверия	к распределению вероятностей
			0,1	выражает

{qj }. Нетрудно заметить, что данный критерий опирается на критерий

Байеса-Лапласа и минмаксный. Если доверие к используемому распределению вероятностей велико, то акцентируется первый критерий, иначе – второй. При c =1 критерий Ходжа-Лемана переходит в критерий Байеса– Лапласа, а при c =0 – в максминный критерий. При использовании данного критерия вероятности появления состояний S j неизвестны, но некото-

рые предположения о распределении вероятностей возможны.

Критерий Гермейера (G-критерий)

FG = max min(uij qj ).

i j

Заметим, что данный критерий обобщает максминный критерий при условии, что вероятности появления состояний S j известны.

Если функция распределения известна не очень надежно, то, следуя G-критерию, получают неоправданно большой риск.

Критерий произведений (Р-критерий)

p

FP = max ∏uij

i j=1

6

ориентирован на величину выигрышей, т.е. на положительные значения величин uij . Если не все uij положительны, то осуществляется сдвиг всех

элементов матрицы uij	+ a , где a >	minuij	, при этом результат примене-
		i , j

ния критерия существенно зависит от значения a . Если выбор константы a затруднителен, то к таким проблемам P-критерий не применим. В результате использования Р-критерия происходит некоторое выравнивание между большими и малыми значениями uij , и, выбирая оптимальный вари-

ант решения с помощью H-критерия, можно при фиксированных состояниях S j получить большую выгоду, чем при использовании минмаксного

критерия, но при этом должна учитываться возможность появления и худших результатов. Следует отметить, что при использовании этого критерия информация о распределении вероятностей не принимается во внимание.

Пример. Некоторая фирма принимает решение о строительстве отеля в одном из курортных мест. Необходимо определить наиболее целесообразное количество комнат в гостинице. Составляют смету расходов по строительству гостиницы с различным количеством комнат, а также рассчитывают ожидаемый доход в зависимости от количества комнат, которые будут сняты. В зависимости от принятого решения – количества комнат в гостинице X ={20,30,40,50} и количества снятых комнат

S ={0,10,20,30,40,50}, которое зависит от множества случайных факторов

и неизвестно фирме, – получают следующую таблицу (табл. 2) ежегодных прибылей.

Таблица 2.

Sj	0	10	20	30	40	50
xi
20	–121	62	245	245	245	245
30	–168	14	198	380	380	380
40	–216	–33	150	332	515	515
50	–264	–81	101	284	468	650

Для определения оптимального количества комнат будем использо-

	вать различные критерии.
	Максминный критерий: max minlik = –121; хопт = 20.
			xi	Sk
	Судя по результатам, данный критерий не применим, так как в этом
	случае от постройки гостиницы следует отказаться.
		6
	Критерий Лапласа: max	1	∑lik	= maxl		= max{153,198,210,193}= 210 ;
					i
	xi	6 k =1		xi

xопт = 40 .

Критерий Гурвица: для разных α можно построить таблицу доходов
по критерию Гурвица H ={hiα }, где hiα	= αmaxlik +(1 −α)minlik (табл. 3).
	k	k

7

Таблица 3.

α	0.1	0.2	0.5	0.9
xi			6
20	–84	–47		206
30	–114	–59	108	325
40	–143	–70	150	442
50	–172	–81	193	560

Оптимальное количество комнат в гостинице в зависимости от α будет следующим (табл. 4).

				Таблица 4.
α	0,1	0,2	0,5	0,9
xопт	20	20	50	50

Критерий Сэвиджа: построим матрицу сожалений (табл. 5). Таблица 5.

Sk	0	10	20	30	40	50
xi				135
20	0	0	0		270	405
30	47	48	47	0	135	270
40	95	95	95	48	0	135
50	143	143	144	96	47	0

max minuik = max {–405, –270, –135, –143} = –135.

xi Sk

Таким образом, выбор предстоит сделать между следующими решениями: по максминному критерию нужно построить 20 комнат; по критерию Лапласа – 40 комнат; по критерию Гурвица – 20 комнат, если заказчик

– пессимист, и 50 комнат, если он оптимист; по критерию Сэвиджа – 40 комнат. Выбор критерия принятия решений является наиболее сложным и ответственным этапом. Он полностью определяется целями ЛПР и должен быть согласован с конкретной спецификой задачи. В частности, если даже минимальный риск не допустим, то следует применять максминный критерий; если, наоборот, определенный риск вполне приемлем и заказчик намерен вложить в некоторое предприятие столько средств, чтобы он потом не сожалел, что вложено слишком мало, то выбирают критерий Сэвиджа.

Практическое задание: подобрать исходную информацию и сформулировать постановку задачи принятия решений в условиях риска. Написать программу, реализующую выбор оптимального варианта с помощью критериев: а) максминного, Сэвиджа, произведений; б) Байеса-Лапласа, Гермейера; в) Гурвица при различных значениях параметра c ; г) ХоджаЛемана при различных значениях параметра c .

Отчет должен включать текст задачи, листинг программы и анализ полученных результатов.

8

Лабораторная работа № 2

ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

Цель – приобрести навыки экономико-математического моделирования и ознакомить с решением задач линейного программирования в среде

EXEL.

Теоретическийминимум

Примечание. Основной теоретический материал рассматривался в рамках дисциплины «Методы оптимизации». Далее остановимся лишь на основных положениях. К детерминированным моделям принятия решений относятся оптимизационные модели, которые в первую очередь нашли широкое применение в экономике, поскольку связаны с планированием целенаправленной деятельности при существующих ограничениях на ресурсы. Несмотря на смысловое разнообразие таких задач, все они формально сводятся к одной общей постановке: найти значения переменных x1 ,x2 ,...,xn , доставляющие максимум

(минимум) заданной скалярной функции f ( x1 ,x2 ,...,xn ) при условиях gi ( x1 ,x2 ,...,xn )[≤,=,≥]bi (i =1,m), которые образуют систему ограничений.

Данная задача является задачей математического программирования, а

функция f ( x1 ,x2 ,...,xn ) называется целевой функцией. Обычно вид функций f и gi (i =1,m) известен, константы bi заданы, величины m,n являются це-

лыми числами (в отдельных случаях между ними устанавливается соотношение m < n ). Специально оговариваются ограничения, выраженные в требова-

ниях неотрицательности и целочисленности xj (j =1,n). В основу классифи-

кации задач математического программирования положены особенности функций f и gi , встречающихся в конкретных исследованиях. Различают два

основных класса задач – задачи линейного и нелинейного программирования. К первым относятся те, в которых и целевая функция f , и все функции

gi (i =1,m) линейны относительно переменных xj (j =1,n), ко вторым – те, в

которыхприсутствуют различного роданелинейности.

Общая форма задачи линейного программирования имеет вид

n

∑сj xj →extr

j=1

∑n aij xj [≤,=,≥]bi (i =1,m),

j=1

xj [≤,≥, нет требования на знак]0,

гдепод extr подразумевается максимум или минимум.

Заметим, что с формальной точки зрения нет необходимости строго различать задачи поиска максимума и минимума, т.к. одна задача сводится к другой изменением знака f напротивоположный.

9

Свойства задач линейного программирования во многом зависят от особенности области допустимых решений, заданной системой ограничений. Она

представляет собой выпуклый многогранник, содержащийся в n . Вершины выпуклого многогранника называются угловыми точками, причем их число конечно. Угловая точка соответствует базисному решению системы, в которой все ограничения являются уравнениями. Известно, что экстремум целевой функции в задаче линейного программирования (если он существует) достигается хотя бы в одной угловой точке многогранника решений. Классическим методом в линейном программировании является симплекс-метод, идея которого заключается в направленном переборе угловых точек, т.е. последовательном переходе от одного базисного решения к другому, при котором происходит улучшение значения целевой функции.

Компьютерная поддержка решения задач линейного программирования осуществляется в среде EXEL с помощью надстройки Поиск решения. Для этого необходимо осуществитьследующую последовательность действий.

1.Ввод исходных данных (коэффициенты целевой функции и ограничений, нижние и верхние границы переменных).

2.Ввод зависимостей для целевой функции и функций из левых частей ограничений задачи.

2.1.Ввод зависимости для целевой функции: поместить курсор в соответствующую значению целевой функции ячейку и выбрать команду

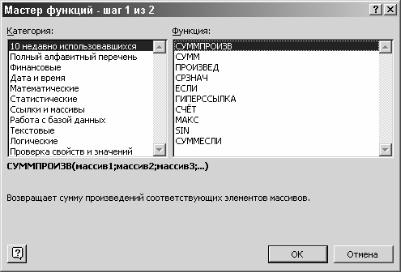
Вставка Функция. На экране появится диалоговое окно Мастер Функций, показанное на рис.1.

Рис. 1.

В разделе Категория представлен список 11 категорий функций. При выборе одной из категорий в списке Функция появляется перечень функций, включенных в эту категорию. Для функции цели выберем категорию

математические, функцию СУММПРОИЗ. Появится Палитра формул

Excel, которая используется для определения аргументов функции, как по-

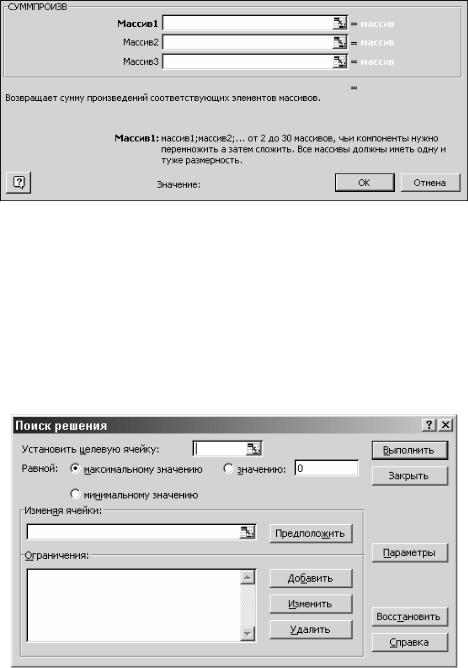
10

казано на рис. 2. В массивы 1 и 2 заносятся диапазоны ячеек, содержащих значения переменных и коэффициенты функции цели.

Рис. 2.

2.2.Ввод зависимостей для левых частей ограничений осуществляется так же, как для целевой функции. При этом в массивы 1 и 2 заносятся диапазоны ячеек, содержащих значения переменных и коэффициенты ограничения.

2.3.Ввод остальных параметров модели. Необходимо выбрать

команду Сервис Поиск решения. На экране появится диалоговое окно Поиск решения, как показано на рис. 3.

Рис.3.

В поле Установить целевую ячейку укажите адрес ячейки, отведенной под значение целевой функции, или щелкните в рабочем листе на этой ячейке. В зависимости от цели задачи – максимизировать или минимизировать значение в этой ячейке – установите переключатель Равной максималь-

ному значению или Равной минимальному значению. Затем определите из-

меняемыеячейки, указавихдиапазониливыделивихнарабочемлисте.

Далее ограничения добавляются по одному и отображаются в окне Ограничения. Для добавления ограничений щелкните на кнопке Добавить. ПоявитсядиалоговоеокноДобавлениеограничения, какнарис. 4.