Задание на лабораторную работу

1. Используя алгоритм электронной цифровой подписи RSA, написать программу генерации, а затем проверки подлинности цифровой подписи под электронным документом на любом языке программирования.

Лабораторная работа №6 Алгоритм Диффи-Хелмана для безопасного обмена ключами

Цель работы: изучить алгоритмы электронной цифровой подписи и освоить их практическое применение.

Теоретическое введение

Данный алгоритм помогает обмениваться секретным ключом для симметричных криптосистем, но использует метод, очень похожий на асимметричный алгоритм RSA.

Алгоритм назван по фамилиям его создателей Диффи (Whitfield Diffie) и Хеллмана (Martin Hellman).

Предположим, что двум абонентам необходимо провести конфиденциальную переписку, а

в их распоряжении нет первоначально оговоренного секретного ключа. Однако, между ними существует канал, защищенный от модификации. Пусть абонентам известны некоторые два числа x и y. Для того, чтобы создать, неизвестный более никому секретный ключ, оба абонента генерируют случайные или псевдослучайные простые числа n и q

Далее отправитель P1 вычисляет и отправляет P2 число А полученное по формуле:

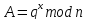
Получатель P2 вычисляет число B и отправляет P1, используя следующую формулу:

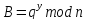
Затем каждый из участников вычисляет секретный ключ, используя следующие формулы:

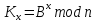
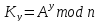
Алгоритм Диффи-Хелмана гарантирует, что 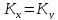. Схематично, работа алгоритма Диффи-Хеллмана представлена на рисунке

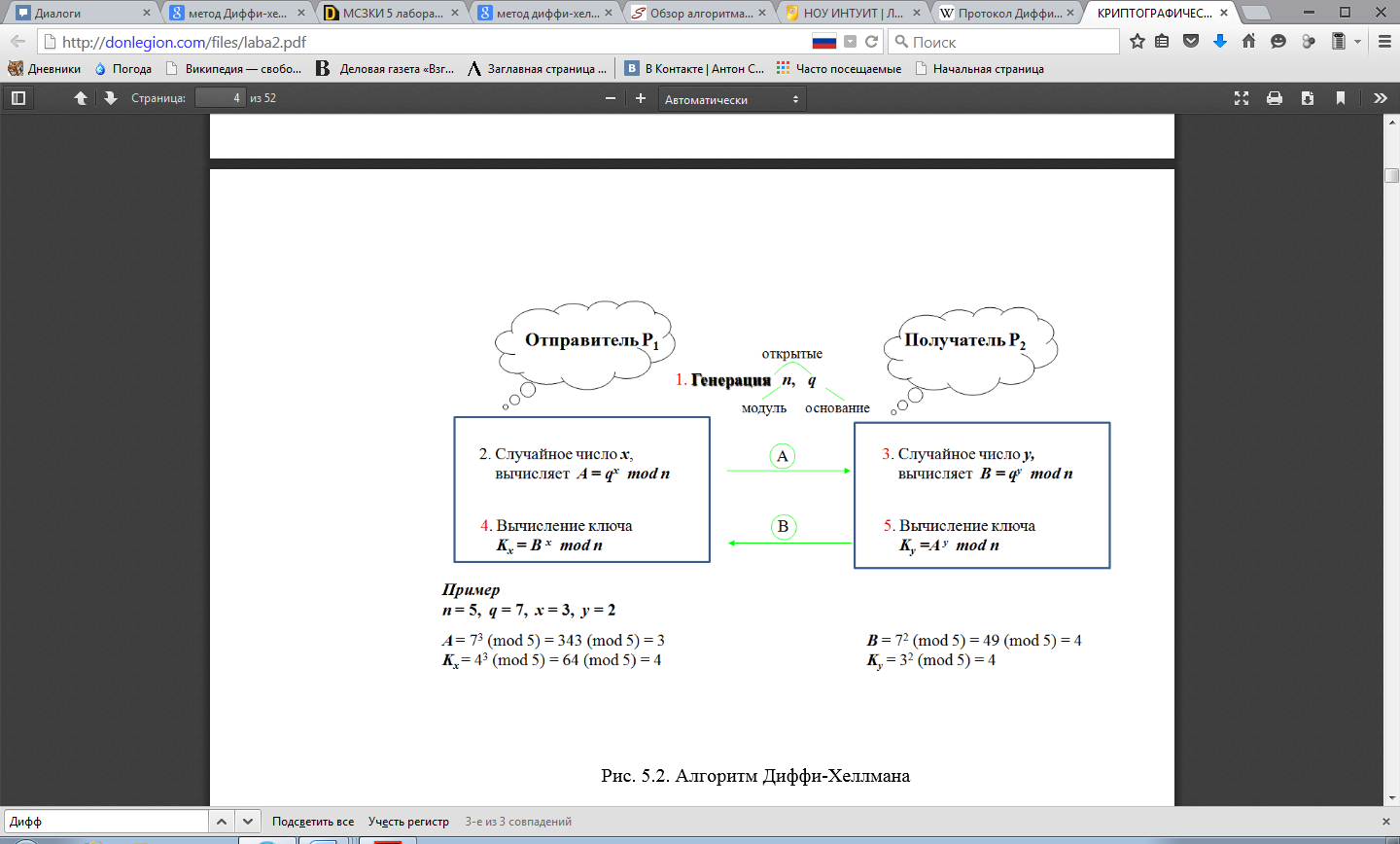
В тоже время данный метод является безопасным, так как даже если злоумышленник перехватит числа p,q,A,B он ни каким образом не сможет получить секретный ключ.

Задание на лабораторную работу

1. Используя алгоритм Диффи-Хелмана, написать программу, которая эмулирует обмен секретными ключами на любом языке программирования.

Список литературы

1. Информационная безопасность и защита информации : учебное пособие / Ю.Ю. Громов, В.О. Драчев, О.Г. Иванова, Н.Г. Шахов. - Старый Оскол : ООО "ТНТ", 2012. - 384 с. - ISBN 978-5-94178-216-1 : 330.00 УДК 004.056.

2. Мельников, В. П. Информационная безопасность и защита информации: учебное пособие / В. П. Мельников, С. А. Клейменов, А. М. Петраков ; под ред. проф. С.А. Клейменова. - 4-е изд., стер. - М. : ИЦ Академия, 2012. - 348.70 с. - ISBN 978-5-7695-6150-4 : 348.70 УДК 004.056.53.

3. Партыка, Т. Л. Информационная безопасность: учебное пособие / Т. Л. Партыка, И. И. Попов. - 4-е изд., перераб. и доп. - М. : ФОРУМ, 2013. - 432 с. : ил. - ISBN 978-5-91134-515-0 : 339.90 УДК 004.056.

4. Емельянова, Н. З. Защита информации в персональном компьютере [Text] : учебное пособие / Н. З. Емельянова, Т. Л. Партыка, И. И. Попов. - М. : ФОРУМ, 2011. - 368 с. : ил. - ISBN 978-5-91134-328-6 : 189.86 УДК 004.056.53.

5. Баричев С.Г., Серов Р.Е. Основы современной криптографии. Учебное пособие. - М.: Машиностроение, 2012. - 754 тc.: ил.

6. Брассар Ж. Современная криптология. Учебное пособие. - М.: ИЛ, 2011. - 362 тc.: ил.

Приложение

Модулярная арифметика

Модулярная арифметика часто изучается в школе как "арифметика часов". Если отсчитать 14 часов от 3 часов после полудня, то получится 5 часов утра следующего дня

3 + 14=5(mod12) или

(3+14) mod 12 = 5

Это арифметика по модулю 12

Обычная запись в модулярной арифметике

а  b(mod n)

читается так "а сравнимо с b по модулю n" Это соотношение справедливо для целых значении a b и nиn0, если и только если

а = b + kn

для некоторого целого k

Отсюда, в частности, следует

n|(a-b)

Это читается как n делит (a-b)

Если а  b(mod n)

то b называют вычетом числа а по модулю n.

Операцию нахождения вычета числа а по модулю n

a(mod n)

называют приведением числа а по модулю n или приведением по модулю.

В нашем примере (3+14) mod 12 = 17 mod 12 =5 или 175(mod l2),

число 5 является вычетом числа 17 по модулю 12.

Набор целых чисел от 0 до (n-1) называют полным набором вычетов по модулю n. Это означает что для любого целого а (а>0) его вычет r по модулю n, есть некоторое целое число в интервале от 0 до (n -1) определяемое из соотношения

r = a+ kn, где k - целое число.

Например, для n = 12 полный набор вычетов

{0,1,2 11}

Обычно предпочитают использовать вычеты

r{0,1,2 n-1},

но иногда полезны вычеты в диапазоне целых

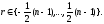
Заметим что

-12(mod 7) -5(mod 7)  2(mod 7)  9(mod 7) и т.д.

Модулярная арифметика аналогична во многом обычной арифметике, она коммутативна, ассоциативна и дистрибутивна. Точнее говоря, целые числа по модулю n с использованием операции сложения и умножения, образуют коммутативное кольцо при соблюдении законов ассоциативности, коммутативности и дистрибутивности.

Фактически мы можем либо сначала приводить по модулю n, а затем выполнять операции, либо сначала выполнять операции, а затем приводить по модулю n, поскольку приведение по модулю n является гомоморфным отображением из кольца целых в кольцо целых по модулю n.

(а + b) mod n = [a(mod n) + D(mod n)] mod n

(a - b) mod n = [a(mod n) - D(mod n)] mod n

(a  b) mod n = [a(mod n)  b(mod n)] mod n

[a  (b + c)] mod n = {[a  b(mod n)] + [a  c(mod n)]} mod n

Криптография использует множество вычислений по модулю n, потому что задачи, типа вычисления дискретных логарифмов и квадратных корней, очень трудны. Кроме того, с вычислениями по модулю удобнее работать, потому что они ограничивают диапазон всех промежуточных величин и результата

Для модуля n длиной k бит промежуточные результаты любого сложения, вычитания или умножения будут не длиннее 2k бит. Поэтому возведение в степень в модулярной арифметике можно выполнить без генерации очень больших промежуточных результатов.

Вычисление степени числа а по модулю n

а^х mod n

можно выполнить как ряд умножений и делений. Существуют способы сделать это быстрее. Поскольку эти операции дистрибутивны, быстрее произвести возведение в степень как ряд последовательных умножений, выполняя каждый раз приведение по модулю. Это особенно заметно, если работать с длинными числами (200 бит и более).

Например, если нужно вычислить

a⁸ mod п,

не следует применять примитивный подход с выполнением семи перемножений и одного приведения по модулю громадного числа

(аааааааа) mod п

Вместо этого выполняют три малых умножения и три малых приведения по модулю.

((a² mod п)² mod п)² mod n

Тем же способом вычисляют

a¹⁶ mod n= (((a² mod n)² mod n² mod n)² mod n

Вычисление

а^x mod n,

где х не является степенью 2, лишь немного сложнее. Двоичная запись числа х позволяет представить число х как сумму степеней 2.

х = 25 ₍₁₀₎1 1 0 0 1₍₂₎, поэтому 25 = 2⁴ + 2³ + 2⁰

Тогда

a²⁵ mod n = (аa²⁴) mod п=(аа⁸а¹⁶) mod п =

= а((а²)²)² (((a²)²}²)² mod n - ((((а² * а)²)²)²a) mod n.

При разумном накоплении промежуточных результатов потребуется только шесть умножений:

(((((((a² mod n)a) mod n)² mod n)² mod n)² mod п)a) mod п.

Этот метод уменьшает трудоемкость вычислении до 1,5хk операций в среднем, где k-длина числа в битах.

Поскольку многие алгоритмы шифрования основаны на возведении в степень по модулю п, целесообразно использовать алгоритмы быстрого возведения в степень.

Расширенный алгоритм Евклида

При заданных неотрицательных целых числах а и b этот алгоритм определяет вектор

{u,, u₂, u₃),

такой, что аu₁+ bu₂= u₃= НОД (a,b)

В процессе вычисления используются вспомогательные векторы (v₁,v₂,v₃), (t₁.t₂,t_з). Действия с векторами производятся таким образом, что в течение всего процесса вычисления выполняются соотношения

, ,.

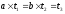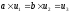Для вычисления обратной величины a^-1(mod n) используется частный режим работы расширенного алгоритма Евклида, при котором b=n, НОД(а,п)=1, и этот алгоритм определяет вектор

{u,, u₂, u₃),

такой, что

, ,

,

.

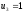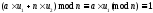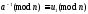Шаги алгоритма:

1. Начальная установка.

Установить (u₁,u₂,u₃): = (0,1,n)_,(v_1,v₂,v₃): = (0,1,a)_.

2. u3=1? Если u₃ = 1, то алгоритм заканчивается.

3. Разделить, вычесть.

Установить q: = [u₃/v₃].

Затем установить

(t,, t₂, t₃): = (u,, u₂, u₃) - (vi, v₂, v₃) - q,

(u,, u₂, u₃): = (v₁, v₂, v₃),

(v₁, v₂, v₃): = (t₁, t₂, t₃).

Возвратиться к шагу 2.