3.4. Алгоритм вычисления определителя -го порядка

1) Получаем в какой-либо строке (столбце), используя свойство 8, нули, кроме одного элемента.

2) Раскрываем определитель по этой строке (столбцу) и приходим к вычислению определителя порядка.

Дальше повторяем пункт 1 и 2, столько раз, пока не придём к определителю 3 порядка, который умеем вычислять.

Пример 3.7. Вычислить .

Решение. Получаем нули в первом столбце (можно во 2 строке, 4 столбце или 4 строке), т. к. один нуль там уже есть.

Удобно, когда в этой строке есть единица. Умножим первую строку на и сложим с 3 строкой (по свойству 8), третью строку сложим с 4 строкой, определитель не изменится.

3.12. Вычислить определители

1) ; 2);

3) ; 4);

5) ; 6).

3.13. Доказать, что для равенства нулю определителя второго порядка, необходимо и достаточно, чтобы его строки были пропорциональны. (коэффициент пропорциональности может быть равен 0).

3.14. Вычислить:

1)2)3)

4) 5)6)

7) 8).

3.15. Доказать, что определитель диагональной матрицы равен произведению диагональных элементов.

3.16. Используя свойства определителя, доказать тождества:

1)

2)

3) Числа 19, 38 делятся на 19. Не вычисляя определителя, докажите, что определитель делится на 19.

3.17. Вычислить:

1)2)3)

4) 5)6)

7) 8).

Вычислить 1) и 2) методом Гаусса.

4.Обратная матрица. Ранг матрицы. Линейная зависимость векторов.

ОБРАТНАЯ МАТРИЦА

Определение 4.1. Квадратная матрица называется вырожденной (особенной), если её определитель равен нулю.

Определение 4.2. Квадратная матрица называется невырожденной (неособенной), если её определитель отличен от нуля.

Определение 4.3. Матрица называетсяобратной для матрицы , если.

Выясним, когда существует обратная матрица.

1 случай. – вырожденная матрица, т. е.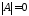, тогда обратной матрицы не существует.

2 случай. – невырожденная матрица, т. е..

Пусть .. Обозначим−присоединённую матрицу, где алгебраические дополнения элементов.

Тогда .

Значит, для невырожденной матрицы обратная матрица существует и равна .

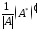Пример 4.1. Найти для.

Решение. 1) Найдём . Значит– невырожденная матрица исуществует.

2) Найдём – присоединённую матрицу, для этого вычислим алгебраические дополнения элементов матрицы.

; ;;

; ;;

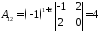; ;; тогда.

Протранспонируем , т. е..

Тогда .

4.1. Доказать, что .

4.2. Найти обратные матрицы и сделать проверку :

1. ; 2.; 3.; 4..

РАНГ МАТРИЦЫ

Рассмотрим прямоугольную матрицу .

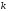Пусть . Выделим в этой матрице строк и столбцов.

Определение 4.4. Минором -го порядка матрицыназывается определитель-го порядка, составленный из элементов, стоящих на пересечении строк истолбцов.

В матрице можно составить миноров-го порядка.

Пример 4.2. Найти все миноры матрицы .

Решение. Т. к., то:

1. миноров 1 порядка (Это элементы матрицы)

2. миноров 2 порядка . Это, например,,,и др.

3. миноров 3 порядка . Это,,,

Если посчитать миноры, то окажется, что:

1) есть отличные от нуля миноры 1 порядка;

2) есть отличные от нуля миноры 2 порядка;

3) миноры 3 порядка все равны 0;

В этом случае будем говорить, что ранг матрицы A равен 2.

Определение 4.5. Рангом матрицы называется наивысший порядок отличных от нуля миноров этой матрицы.

Таким образом, если ранг матрицы равен , то среди миноров матрицы есть по крайней мере один минор-го порядка отличный от нуля, в то время как все миноры-го порядка и выше равны нулю. Ранг только нулевой матрицы равен нулю.

Ранг матрицы будем обозначать .

Для вычисления ранга матрицы существует метод (метод Гаусса), не требующий вычисления определителей, основанный на элементарных преобразованиях.

Определение. 4.6. Элементарными преобразованиями матрицы называются следующие преобразования:

1) транспонирование матрицы;

2) перестановка строк или столбцов;

3) умножение всех элементов строки (столбца) на любое число, отличное от нуля;

4) прибавление к элементам строки(столбца) соответствующих элементов строки (столбца), умноженных на одно и то же число.

Теорема 4.1. (Об элементарных преобразованиях).

При элементарных преобразованиях матрицы ее ранг не меняется.