3 семестр ЭКТ / Физика. Оптика / Методические материалы и лекции / Оптика. Методика решения задач

42	ОПТИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

Решением этой системы уравнений являются такие действительная (n′) и мнимая (n′′) части комплексного показателя прелом-

ления n = n′−in′′, зависимость которых от частоты ω определяется формулами:

				1						σ			2
(n′)	2															,
			=					1 +							+1
				2
									ε0ω
				1						σ				2
(n′′)		2
			=					1 +							−1 .
				2
										ε0ω

С учетом (2.37) уравнения для волн Е и Н представимы в виде:

′	(2.38)
E(r,t )= E0 (r) ei(ωt−k r) ,
′	(2.39)
H (r,t )= H0 (r) ei(ωt−k r) .

Амплитуды волн (2.38) и (2.39)

E0 (r) = E0e−k′′r , H0 (r) = H0e−k′′r

экспоненциально убывают в направлении k″. Фазовая скорость волн (2.38) и (2.39) определяется действительной частью показателя преломления:

		v =			c		еk′,
					′
					n			проникновения
тогда как мнимая часть характеризует глубину
волны в проводящую среду:	1				c
=			=
							.	(2.40)
	k	′′			′′
				n ω

Если σ = const, то по мере увеличения частоты ω показатель n″ убывает, стремясь к нулю, и прозрачность проводящей среды повышается.

В соответствии с (2.36) и (2.37) вектор k вещественный, если проницаемость ε(ω) вещественная и положительная, или k′ k″

(как в случае полного внутреннего отражения света на границе сред, см. гл. 7). Если векторы k′ и k″ неколлинеарны, то плоские волны (2.38) и (2.39) неоднородные.

Гл. 2. Уравнения Максвелла. Электромагнитные волны.

43

Чтобы найти связь между Е и Н для электромагнитной волны в проводящей среде, подставим (2.38) и (2.39) в уравнения Максвелла. В результате получим:

−[k, H]= ωε0E 1−i εσ0ω ,

	[k, E]=	ω	H ,
		ε0c2
	(k, E)= 0 ,

(k, H)= 0 .

Таким образом, и в этом случае электромагнитная волна – поперечная, т.е. векторы Е, Н и k ( k′↑↑ k′′ ) взаимно ортогональны, однако волна Е опережает по фазе волну Н на

ϕn′′

=arctg n′ .

В частности, если	σ	>>1, то	n	′′	≈ 1 и ϕ =	π .
				′
	ε0ω		n			4

В соответствии с формулой (2.24):

μ0 H0 = n ε0 E0 ,

или

μ0 H0 = ε0 ((n′)2 + (n′′)2 )E0 .

Интенсивность световой волны в проводящей среде убывает по закону

I = I0e−2k′′r ,

где

ε0 (n′)2 + (n′′)2 E2

I0 = 2 0 cosϕ c .

С формальной точки зрения затухание волны имеет место, если ε′′ ≠ 0 . В диэлектрической среде без дисперсии поляризация Р (а следовательно, и смещение связанных зарядов из положения равновесия) и поле Е изменяются синфазно, а скорость зарядов и Е сдвинуты по фазе друг относительно друга на π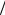2 . Поэтому сред-

няя по времени мощность сил электрического поля равна нулю. В случае же проводящей среды скорость свободных зарядов и Е из-

44	ОПТИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

меняются в фазе, поэтому затухание волн обусловлено так называемыми «потерями на джоулево тепло».

4. Электромагнитные волны в проводящей среде (ε ≠ 1)

В этом случае

′		′′			σ
			= (1	+ χ)−i ε0ω .
ε(ω)= ε	−iε

Для действительной и мнимой частей комплексного показателя преломления ( n = n′−in′′) имеем:

1

σ

2

(n′)2 =

ε′2

+

+ ε′

,

2

ε0ω

1

σ

2

(n′′)2 =

ε′2

+

−ε′ .

2

ε0ω

Замечание. Если ε′′ = 0 , а ε′ < 0 , то k′ = 0 , а k′′ ≠ 0 . В этом случае диссипация энергии отсутствует, однако волна вглубь среды не распространяется (как, например, в случае отражения от плазмы при низких частотах). Если же ε′′ ≠ 0 (инерционность отклика среды), то затухание интенсивности будет обусловлено работой электрического поля E, затрачиваемой на индуцирование токов связанных зарядов.

2.2. Задачи с решениями

Задача 2.2.1. В вакууме распространяется плоская электромагнитная волна E = ey E0 cos(ωt −kx) с частотой ω = 1,5 108 с−1,

где ey – орт вдоль оси у. Найти амплитуду Е0 напряженности элек-

трического поля волны в точке с координатой x =10 м в момент t = 40 нс, если в той же точке и в тот же момент времени Н = 0,2 еz[А м−1].

Решение

В соответствии с (2.30):

cε0 E0 = H0 .

Поскольку вектор k ориентирован вдоль оси х, то

Гл. 2. Уравнения Максвелла. Электромагнитные волны.

45

H= ez H0cos(ωt − kx)= ez H0cos ωt − ω x = ez H0cosϕ,

c

x

8

−9

10

где ϕ = ω t

−

=1,5

10

40 10

−

=1, и следовательно,

8

c

3

10

cos ϕ ≈ 0,54 .

Таким образом,

H0

=

H

=

0,2

= 0,37 А/м,

cosϕ

0,54

а искомая амплитуда:

0,37

E0

=

=139 В/м.

108 0,885 10−11

3

Ответ: E0 = 139 В/м.

Задача 2.2.2. Шар, находящийся в немагнитной среде с диэлектрической проницаемостью ε = 4,0 , облучается плоской элек-

тромагнитной волной с амплитудой Е0 = 200 В/м. Найти радиус шара R, если за время t =1 мин на него падает энергия 5 кДж. Длина волны λ << R .

Решение	t , равна
Энергия, падающая на шар за время
W = I S	t ,

где I – интенсивность световой волны, S = πR2 – площадь большого круга шара. Согласно (2.31) интенсивность световой волны равна

							ε	0	εE2
				I =						0		υ,
									2
где υ= c ε − скорость света в среде. Таким образом,
			R =						2W						,
					πΔtε					0	εE2c
или											0
R =				2 5 103												= 0,5 м.
		60	8,85	10		−12			2		4 10		4		8
3,14															3 10

Ответ: R = 0,5 м.

46	ОПТИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

Задача 2.2.3. Исследовать структуру светового поля, создаваемого двумя плоскими, линейно поляризованными, когерентными волнами, бегущими в вакууме под углом α друг к другу.

Решение

Пусть волновые векторы k1 и k2 лежат в координатной плос-

кости хOz под углом θ к оси Oz

( α = 2θ , см. рис. 2.2). Тогда

			k1 ={kx , 0, kz },
			k2 ={− kx , 0, kz },
		где	kx = k sin θ,		kz = k cos θ ,
Рис. 2.2. Ориентация волновых		k = 2π λ = ω c , с –			скорость света
		в вакууме.
векторов k1 и k2 в плоскости x0z			Уравнения для компонент Е и
		Н каждой из волн могут быть за-
		писаны (при соответствующем вы-
боре начала отсчета) следующим образом:
E = E ei(ωt−k1r) , H = H ei(ωt−k1r),
1	10		1	10

E2 = E20ei(ωt−k2r) , H2 = H20ei(ωt−k2r) .

Рассмотрим сначала случай, когда плоскости поляризации обеих волн совпадают с плоскостью х0z (рис. 2.2). Так как электромагнитные волны – поперечные, то:

E10 ={E0cosθ, 0, − E0sinθ}, E20 ={E0cosθ, 0, E0sinθ}

H10 ={0, H0 , 0},

H20 ={0, H0 , 0},

причем H

0

=

ε0

E = cε

E

. Поскольку

k r = k

x

x + k

z

z

и

μ

0

0

0

0

1

k2r = −kx x + kz z , то проекции векторов E и

H на координатные

оси:

Ex = E1x + E2 x = E0cosθ (eikx x + e−ikx x ) ei(ωt−kz z) ,

Ez = E1z

+ E2 z = E0sinθ (eikx x −e−ikx x ) ei(ωt−kz z) ,

Гл. 2. Уравнения Максвелла. Электромагнитные волны.

47

H y = H1 y + H2 y = H0 (eikx x + e−ikx x ) ei(ωt−kz z).

Переходя от комплексной формы записи к вещественной, получим:

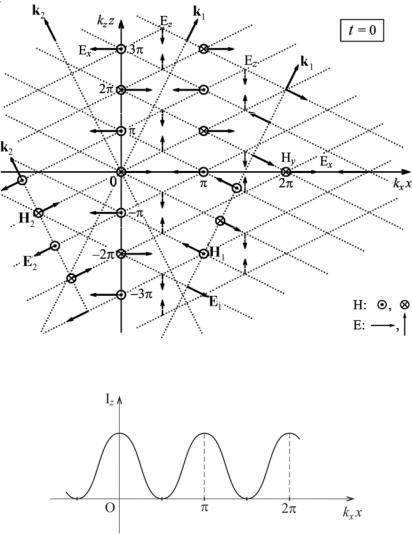
Ex = 2E0cosθ cos(kx x) cos(ωt − kz z), Ez = −2E0sinθ sin (kx x) sin (ωt − kz z),

H y = 2H0cos(kx x)cos(ωt - kz z).

Эти уравнения позволяют рассматривать результирующее поле как суперпозицию двух волн: неоднородной (Ex , H y ) -волны,

бегущей вдоль оси 0z, и стоячей (Ez , H y ) -волны.

На рис. 2.3 показана ориентация векторов Е и Н в некоторых

точках плоскости х0z в момент времени						t = 0 . Фазовая скорость
бегущей (Ex , H y ) -волны
υz =	ω	=	ω	=		c
			k cos θ		cos θ
	kz
больше скорости света (при θ ≠ 0 ),				а скорость переноса энергии
вдоль оси 0z

uz = c cosθ

меньше скорости света, причем uz υz = c2 . Вектор Пойнтинга, ха-

рактеризующий мгновенное распределение плотности потока энергии в пространстве:

S = [E, H]= {− Ez H y, 0, Ex H y },

лежит в плоскости х0z и изменяется с удвоенной частотой 2ω:

Sx = E0 H0sinθ sin (2kx x) sin 2(ωt − kz z) , Sz = 4E0 H0cosθ cos2 (kx x) cos2 (ωt − kz z).

Для соответствующих направлений интенсивность поля равна:

Ix =			Sx		T	= 0 ,			(k		x).
I	z	=	S	z	T	= 2E H	0	cosθ cos2		x
						0
Таким образом,	Iz		достигает				максимума			в плоскостях

kx x = 0, ± π, ± 2π,... (см. рис. 2.4), которые являются узловыми для стоячей (Ez , H y ) -волны, т.е. для этих плоскостей тангенциальная составляющая E всегда равна нулю.

48	ОПТИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

Рис.2.3. Ориентация векторов E и H в различных точках пространства в момент времени t = 0

Рис. 2.4. Распределение интенсивности светового поля Iz вдоль оси x

Эта особенность структуры электромагнитного поля в рассматриваемом случае может быть положена в основу анализа распространения волн в металлических волноводах (концепция Бриллюэна). В частности, при фиксированном расстоянии а между двумя узловыми плоскостями незатухающее распространение волн вдоль оси 0z возможно, только если sin(kxa)= 0 , т.е. для дискрет-

	Гл. 2. Уравнения Максвелла. Электромагнитные волны.					49
	ного набора			kx = n π ( n =1, 2,..). А так как	kx = ksinθ =	2π	sinθ и
		nλ		a		λ
	sinθ =		≤1,	то длина волны не может быть больше 2а. Если
		2a

λ < 2a , то для фиксированных а и λ угол θ может принимать лишь

nm дискретных значений: n	=	2a				([ ] − целая часть		2a	).
m								λ
		λ
В случае, когда векторы E1				и E2			параллельны оси 0у, струк-

тура светового поля аналогична описанной выше, но координаты х узловых плоскостей стоячей волны оказываются иными. (Найдите их самостоятельно!)

Расстояние между двумя соседними максимумами Iz (рис. 2.4) равно:

x =	π	=	π	=	λ	=	λ	,
	kx		ksinθ		2sinθ		2sin (α 2)

а при малых углах α – x ≈ λα.

Задача 2.2.4. Найти силу давления F плоской световой волны на шар радиусом R, если интенсивность волны равна I0, а поверхность шара рассеивает падающее излучение равномерно по всем направлениям.

Решение

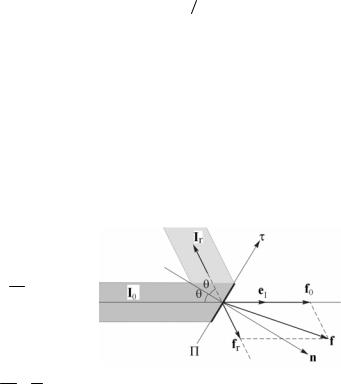
Рассмотрим сначала случай, когда плоская световая волна падает на пластинку площадью σ под углом θ (рис. 2.5).

Так как интенсивность световой волны равна I0 , то среднее

значение объемной плотности энергии электромагнитного поля:

w = Ic0 ,

где с – скорость волны, а среднее значение объемной плотности импульса:

wP = cI02 = wc .

Рис. 2.5. Падающий и отраженный световые пучки и силы, действующие на пластинку П

50	ОПТИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

Следовательно, за время t волна «приносит» к пластинке импульс

P = w c	t (σ cos θ) e	I	=	I0	tσcos θ e	I	,
P				c

где eI – единичный вектор в направлении распространения света.

Если свет, падающий на пластинку, полностью поглощается, то на пластинку будет действовать сила

f0 =	P =			I0		σcosθ eI ,
	t			c
проекции которой на направления n и τ равны соответственно
fn = f0cosθ и fτ = f0sinθ ,
а давление света на пластинку:
p =	fn		=		I0		cos2θ .
	σ
					c
При частичном отражении света от пластинки под углом θ

( Ir = ρI0 , ρ≤1 – коэффициент отражения по интенсивности) пла-

стинка будет получать дополнительный импульс («импульс отдачи»), причем

fr = rf0 .

В результате сила давления f (см. рис. 2.5) равна

f= f0 + fr ,

аформулы для проекций этой силы на различные направления имеют вид:

fn = (f , en )= (1 + ρ)Ic0 σcos2 θ,

fτ = (f, eτ)= (1 −ρ) Ic0 σsin22θ .

Вслучае рассеяния пластинкой падающего на нее света равно-

мерно по всем направлениям сила fr (в силу симметрии геометрии

рассеяния) будет направлена вдоль нормали n . Найдем величину этой силы.

Гл. 2. Уравнения Максвелла. Электромагнитные волны.

51

Пусть пластинка площадью σ рассеивает за время t энергию W равномерно по всем направлениям в телесном угле 2π (левое полупространство на рис. 2.6). В направлении (θ, ϕ) в телесный угол

dΩ = sinθ dθ dϕ за это время «уносится» импульс

dP(θ, ϕ)=		W	dΩ	eθ .
	c
		t 2π

Рис. 2.6. Рассеяние падающего на пластинку света в направлении (θ, ϕ)

Суммируя проекции dP на
направление нормали n , полу-
чим:
2π π 2		π 2		W sin θ cos θ dθ =						1	W .
P = ∫	∫ dP cos θ =	∫
										2
0	0	0		c							c
(ϕ) (θ)
Следовательно, при рассеянии света сила «отдачи» равна
			fr =		P	=	1		W
					t		2 c		t

и направлена вдоль нормали n к пластинке.

Теперь для получения ответа на вопрос, сформулированный в задаче, рассмотрим элемент поверхности шара, ориентированный под углом θ к вектору I0 (см. рис. 2.7). Площадь этого элемента равна

dσ = R2sinθ dθ dϕ.

Так как элементом dσ за время t рассеивается энергия W = I0 dσ cosθ t , то на него действует сила:

df = df0 + dfr ,

причем

df0 = Ic0 dσcosθ eI ,