3 семестр ЭКТ / Аннотации с дисциплине / lect_M8_vm2_x_MatAn_x

,

имеющее вид

.

Произведения и дают частные решения

. (8)

Из начального условия (3) получаем, что . Второе начальное условие (4) дает

Вычисляем

,

откуда

.

Окончательно решение поставленной задачи имеет вид:

.

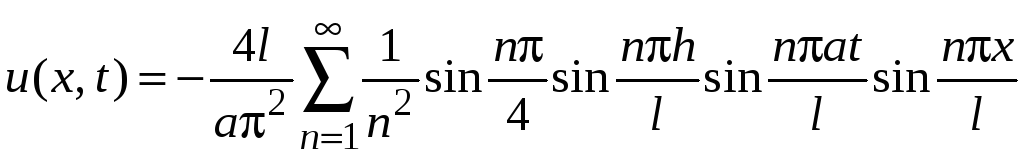Благодаря множителю , каждый четвертый член ряда при обращается в ноль.

Отметим одну особенность решений гиперболических уравнений. Если для задачи теплопроводности частные решения – это некие функции, из которых формируется общее решение, то в случае уравнения колебаний функции (8) имеют дополнительно явный физический смысл: каждая из них представляет собой реальный возможный вид колебания струны. При таких колебаниях все точки струны одновременно достигают своего максимального отклонения в ту или иную сторону и одновременно проходят положение равновесия. Такие колебания струны называются стоячими волнами. На рисунках показана форма струны в различные моменты времени для случая , . Неподвижные точки называются узлами стоячей волны. Посередине между узлами располагаются точки, в которых отклонения достигают максимума; такие точки называют пучностями.

В рассмотренном выше примере в точке оказываются узлы волн с номерами . Для всех этих волн в точке струна неподвижна, поэтому удар молоточка по струне в окрестности этой точки не вызывает появления волн с .

Теперь перейдем к рассмотрению более общего случая для уравнений параболического и гиперболического типов, когда и уравнения и краевые условия оказываются неоднородными. Методы решения таких задач для обоих типов уравнений практически одинаковы. Мы рассмотрим их применительно к уравнению параболического типа, где все преобразования чуть проще из-за того, что начальное условие только одно.

Самая общая постановка задачи такова: найти решение уравнения

,

если или ее производная при или равны соответственно и ; начальное условие, как обычно, имеет вид .

Чтобы решить эту задачу, вначале необходимо рассмотреть неоднородное уравнение с нулевыми граничными и нулевым начальным условиями. Начнем с частного случая, когда есть функция только от .

. (9)

Граничные условия возьмем как и выше:

, (10)

и нулевое начальное условие

. (11)

Величина в правой части уравнения (9) представляет собой плотность тепловых источников в стержне, причиной которых может быть, например, тепло, возникающее в стержне при пропускании через него электрического тока. Зависимость плотности этих источников от может быть связана с зависимостью величины электрического сопротивления стержня от координаты .

Будем искать решение уравнения (9) в виде суммы двух функций , подстановка которых в уравнение дает

.

Если потребовать, чтобы удовлетворяла однородному уравнению , тогда функция может быть найдена из условия двукратным интегрированием. Константы интегрирования выберем так, чтобы удовлетворяла граничным условиям: и . Тем самым функция оказывается однозначно определенной. При этом также удовлетворяет нулевым граничным условиям (10), а подстановка в начальное условие дает

или.

Итак, для функции получена стандартная задача в виде однородного уравнения, однородных граничных условий и некоторого ненулевого начального, а сумма и будет решением задачи (9-11).

Литература к лекциям 47-48.

1.Я.С.Бугров, C.М. Никольский. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. – М.: Дрофа, 2005.

19