3 семестр ЭКТ / Аннотации с дисциплине / lect_M8_vm2_x_MatAn_x

Модуль 8

«Уравнения в частных производных»

дисциплины

«Математический анализ»

Содержание лекционного материала

Лекция 46. Понятие о дифференциальных уравнениях в частных производных. Линейные уравнения в частных производных второго порядка.

Основные понятия: дифференциальное уравнение в частных производных, канонический вид дифференциальных уравнений, канонический вид уравнений гиперболического, эллиптического и параболического типов.

Уравнение называется дифференциальным, если оно вместе с одной или несколькими независимыми или зависимыми переменными содержит также производные последних по первым.

Различают два типа дифференциальных уравнений:

1. обыкновенные дифференциальные уравнения,

2. дифференциальные уравнения c частными производными.

Порядок дифференциального уравнения – порядок старшей входящей в него производной.

Дифференциальное уравнение называется линейным, если зависимые переменные и их производные входят в него лишь в первой степени и не умножаются друг на друга.

Будем рассматривать линейные дифференциальные уравнения второго порядка относительно двух или трех переменных.

Будем обозначать производные по соответствующей координате нижним индексом, т.е. , , . Общий вид дифференциального уравнения от двух переменных:

. (1)

Здесь предполагается, что неизвестная функция – функция двух переменных. Если , то уравнение (1) называют однородным (иначе неоднородным). Если коэффициенты a, b и с не зависят от переменных x и y, то уравнение (1) называют уравнением с постоянными коэффициентами.

Решением (интегралом) дифференциального уравнения является функция независимых переменных и произвольных постоянных, которая при подстановке в уравнение превращает его в тождество.

Дифференциальное уравнение называется интегрируемым в конечном виде, если его решение может быть представлено в явной форме при помощи элементарных функций (алгебраических, логарифмических, показательных, тригонометрических) и конечного числа квадратур (определенных интегралов).

Замена координат требуется в том случае, когда необходимо представить уравнение в каноническом виде (стандартный вид уравнения, который используется для нахождения общего решения) или при переходе в систему координат, которая наиболее точно отражает геометрию описываемого процесса или явления, что упрощает решение.

Запишем уравнение (1) в виде

. (2)

Здесь x и y – независимые переменные, пусть , – новые переменные. Для перехода из системы координат x и y к системе координат  и  необходимо выразить производные по x и y через производные по  и . Используя правила дифференцирования сложной функции, получаем

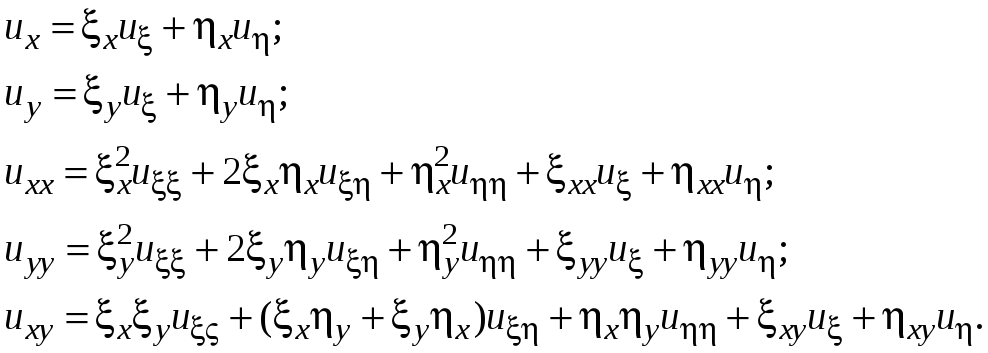(3)

Подставляя производные (3) в уравнение (2) получаем уравнение в новых переменных. При этом обычно требуют, чтобы новые переменные были линейно независимыми, что приводит к необходимости выполнения условия неравенства нулю якобиана преобразования, т.е.

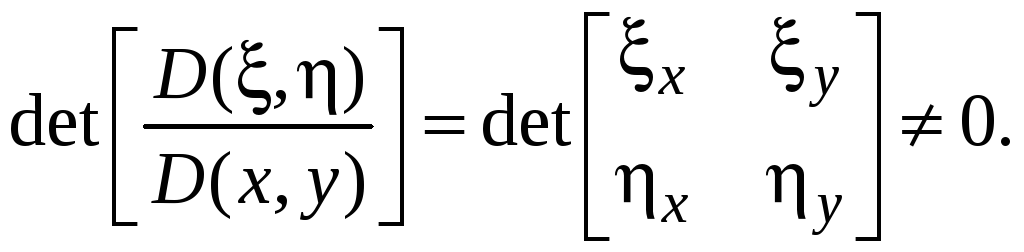(4)

Для установления канонического вида рассматривают дискриминант уравнения (1) или (2):

. (5)

Если , то уравнение называют гиперболическим, – эллиптическим, если – параболическим. В случае, когда не во всей области определения x и y дискриминант имеет одинаковый знак, выделяют области гиперболичности, эллиптичности и параболичности уравнения. Соответственно в этих областях решения уравнения (1) или (2) могут существенно отличаться.

Замена переменных, приводящая к каноническому виду, выполняется при помощи решения системы уравнений

(6)

Это обыкновенные дифференциальные уравнения и в случае постоянных коэффициентов их решение находится элементарно. Решая эти уравнения и выражая решения в виде двух функций и , получаем две переменных  и , которые и приводят исходное уравнение к каноническому виду.

Рассмотрим канонический вид уравнения при различном знаке дискриминанта.

1. Пусть , тогда система (6) имеет два линейно независимых решения, для уравнения с постоянными коэффициентами – , , преобразуя уравнение (2) в соответствии с правилами (3) получим первый канонический вид гиперболического уравнения

. (7)

В случае, когда , имеем простейшее решение

, (8)

где f₁ и f₂ – некоторые функции.

За независимые также можно принять переменные и , тогда исходное уравнение преобразуется во второй канонический вид гиперболического уравнения

. (9)

2. При уравнения (6) имеют комплексно сопряженные решения, и действительные новые линейно независимые переменные можно выбрать как мнимую и действительную части этих решений. Пусть (x,y) решение какого-либо из уравнений (6), тогда , . В результате преобразований получим канонический вид дифференциального уравнения эллиптического типа:

. (10)

3. Наконец, когда , уравнения (6) совпадают. В этом случае за переменную  принимают решение (6), а за переменную  произвольную линейно независимую функцию. Канонический вид дифференциального уравнения параболического типа будет иметь вид:

. (11)

Литература к лекции 46

1.Я.С.Бугров, C.М. Никольский. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. –М.: Дрофа, 2005.

Лекции 47-48. Метод Фурье решения линейных уравнений в частных производных.

Основные понятия: метод Фурье, уравнение теплопроводности, начальные условия, граничные условия.

Метод Фурье или метод разделения переменных является одним из наиболее распространенных методов решения уравнений с частными производными. Мы начнем изложение этого метода с задачи о распространении тепла вдоль тонкого стержня конечной длины, боковая поверхность которого теплоизолирована.

Соответствующее уравнение является уравнение параболического типа

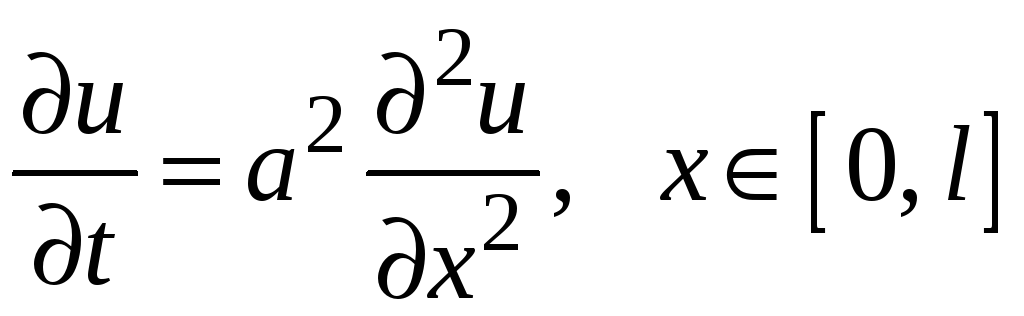, (1)

где – температура сечения с координатой в момент времени .

Пусть левый конец стержня поддерживается при нулевой температуре, то есть , а правый торец теплоизолирован. Поток тепла вдоль стержня выражается формулой , поэтому условие теплоизолированности заключается в том, что .

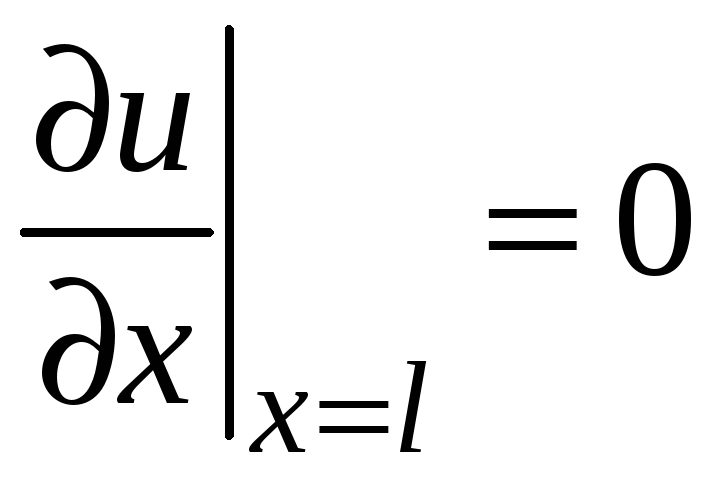Итак, граничные условия данной задачи имеют вид:

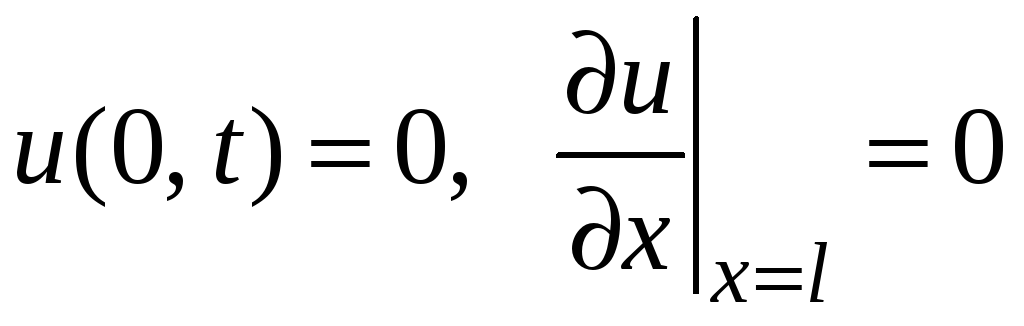. (2)

Чтобы задача была полностью определена, необходимо задать начальное условие, то есть температуру стержня в начальный момент времени:

. (3)

Будем сначала искать частные решения уравнения (1), не равные тождественно нулю, и удовлетворяющие граничным условиям (2), в виде произведения

. (4)

Подставив (4) в уравнение (1), получим

или

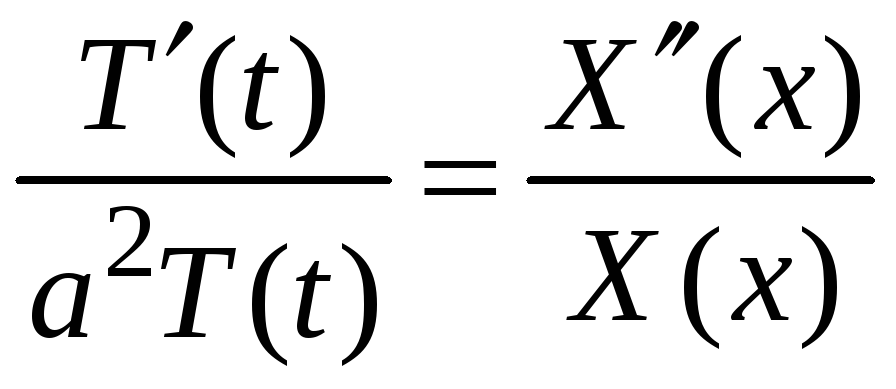. (5)

Последнее равенство, левая часть которого зависит только от , а правая – только от , возможно лишь в том случае, если обе части его не зависят ни от , ни от , то есть представляют собой одну и ту же постоянную. Обозначив ее через , из (5) получим два обыкновенных дифференциальных уравнения

. (6)

Подстановка (4) в граничные условия (2) дает:

и .

Если равна нулю в любой момент времени, то решение (4) становится тождественно равным нулю. Чтобы получить нетривиальные решения вида (4), надо взять граничные условия в виде .

Таким образом, мы приходим к следующей задаче: найти ненулевые решения уравнения

, (7)

удовлетворяющие граничным условиям

. (8)

Но это – частный случай задачи Штурма – Лиувилля.

Собственными значениями, то есть значениями параметра , при которых задача (7 – 8) имеет нетривиальные решения, являются величины

,

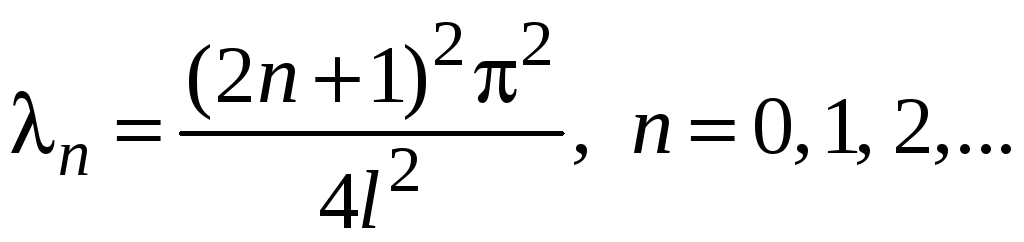а собственными функциями, или соответствующими нетривиальными решениями – функции

.

Квадрат нормы всех собственных функций этой задачи одинаков и равен .

При общее решение уравнения (6) имеет вид

,

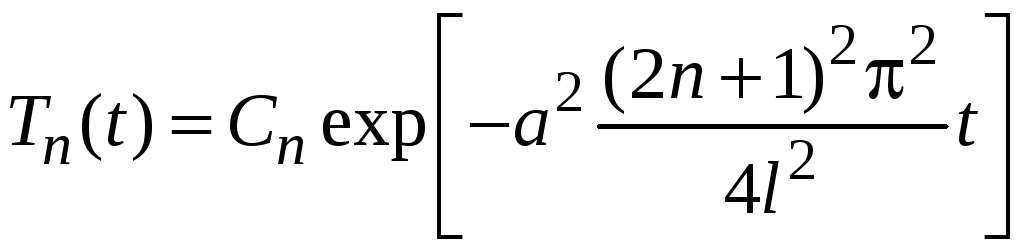где –произвольные постоянные.

Таким образом, функции

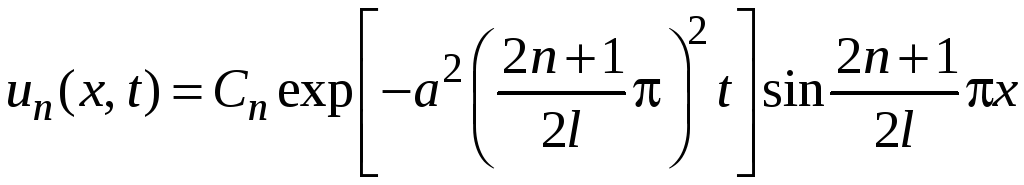
удовлетворяют уравнению (1) и граничным условиям (2) при любых .

В силу линейности и однородности уравнения (1) всякая конечная сумма решений будет также решением. То же справедливо и для ряда

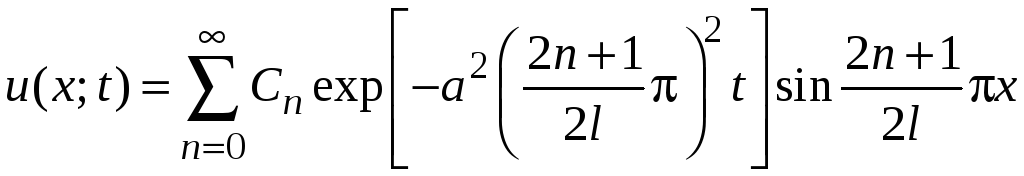, (9)

если он сходится и его можно почленно дифференцировать по и дважды по . Поскольку каждое слагаемое ряда (9) удовлетворяет нулевым граничным условиям (2), то этим условиям будет удовлетворять и сумма ряда, то есть функция . Осталось определить постоянные так, чтобы удовлетворялось начальное условие (3).

Положив в (9) и приравняв полученный ряд функции , получим

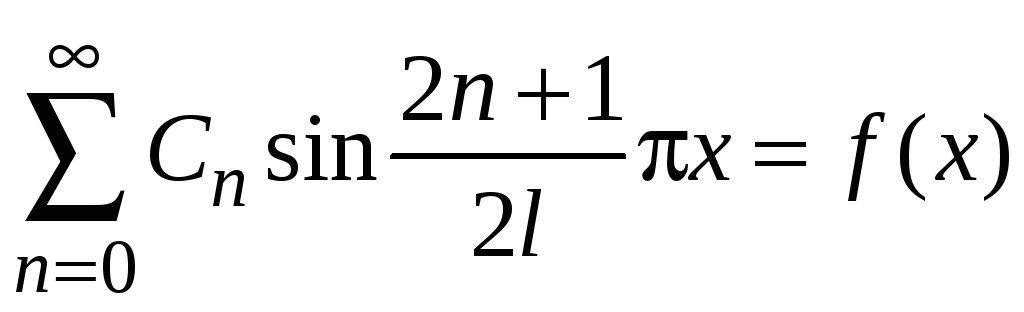. (10)

Любая кусочно-непрерывная функция может быть разложена в ряд по собственным функциям задачи Штурма - Лиувилля, и этот ряд сходится к в смысле средне-квадратического приближения. При этом коэффициенты в (10) вычисляются по формулам

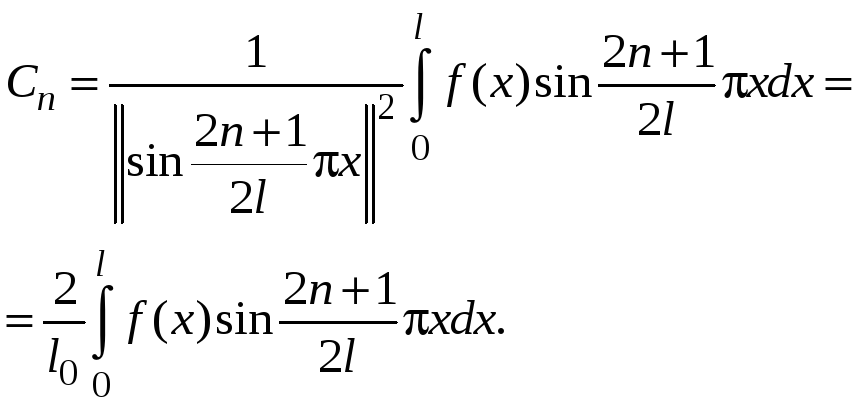(11)

Итак, решением задачи (1 – 3) является ряд (9), где коэффициенты вычисляются по формулам (11).

Продолжим рассмотрение задачи о распространении тепла в стержне, но уже не конечном, а бесконечном:

. (12)

Если стержень очень длинный, то на процессы в его средней части главное влияние оказывает начальное распределение температуры; влияние условий на концах стержня в течение довольно длительного времени почти не будет сказываться, поэтому в задачах такого типа стержень считают бесконечным.

Краевые условия при этом отпадают, а на искомую функцию накладываются только начальное условие

. (13)

Стандартный метод разделения переменных дает два обыкновенных дифференциальных уравнения

, (14)

. (15)

Из-за отсутствия граничных условий на величину параметра накладывается только одно условие: , так как при решение уравнения (14) неограниченно растет с ростом , что физически невозможно. Частным решением (14) является функция , а общим решением (15):

.

Итак, частное решение вида уравнения (12) записывается следующим образом:

,

или после замены , где :

. (16)

Выражение (16) при любом значении является решением уравнения (12), и мы можем, конечно, для каждого значения выбирать различные значения для и . Это означает, что и могут быть произвольными функциями от : и . С учетом этого, семейство частных решений (16) уравнения (12) может быть записано в виде

.

В силу линейности и однородности уравнения (6.1) функция

(17)

также является решением (12). Начальное условие (13) дает:

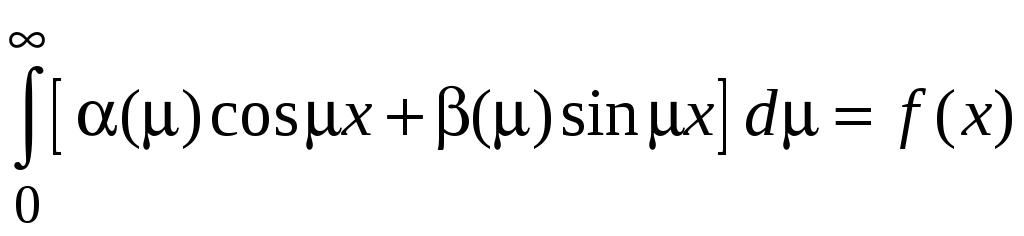. (18)

Если кусочно-непрерывна на любом конечном отрезке и абсолютно интегрируема на всей вещественной оси, что в физических задачах всегда выполняется, то выражение (18) – это разложение с точностью до коэффициента функции в интеграл Фурье. Функции и определяются при этом по формулам

,

.

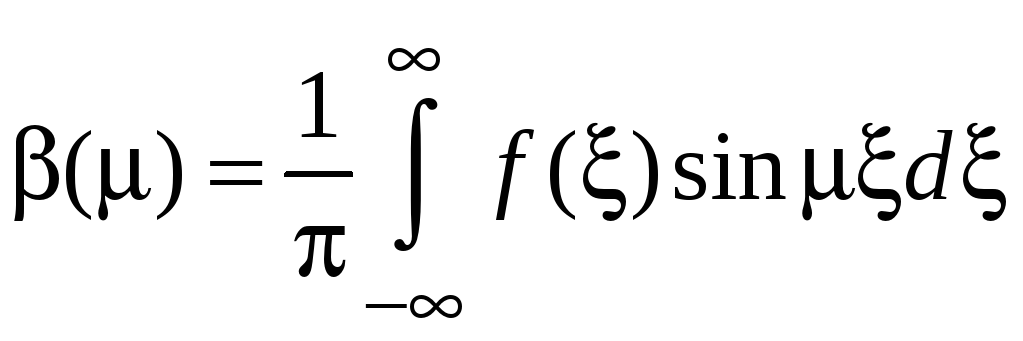Подстановка этих выражений в (17), ряд тригонометрических преобразований и изменение порядка интегрирования приводят к следующему представлению решения уравнения (12):

.

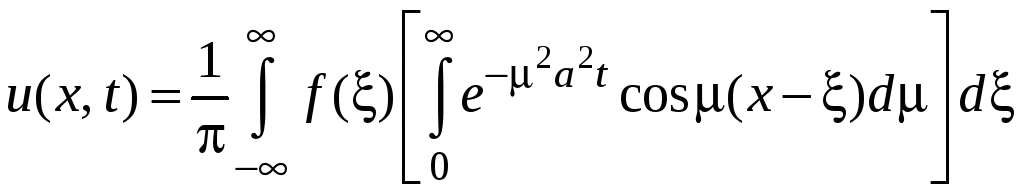Вычислим внутренний интеграл:

.

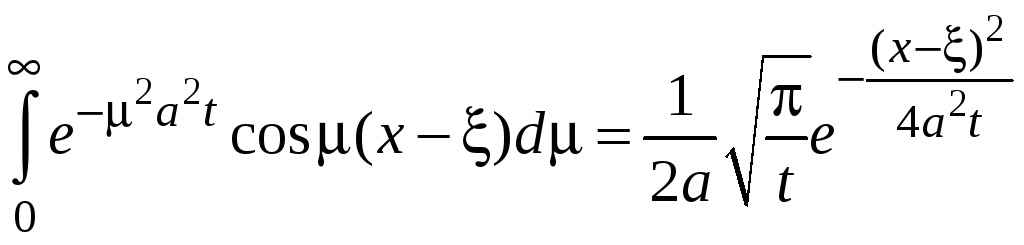Подстановка этого выражения для интеграла в предыдущую формулу позволяет представить решение задачи (12 – 13) в виде

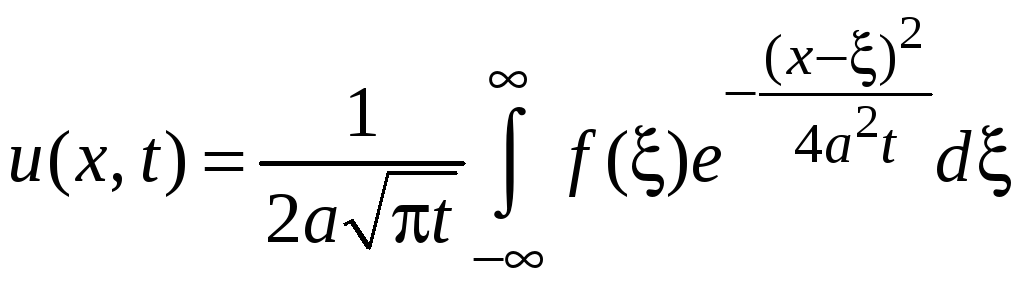. (19)

Полученное выражение может быть представлено следующим образом:

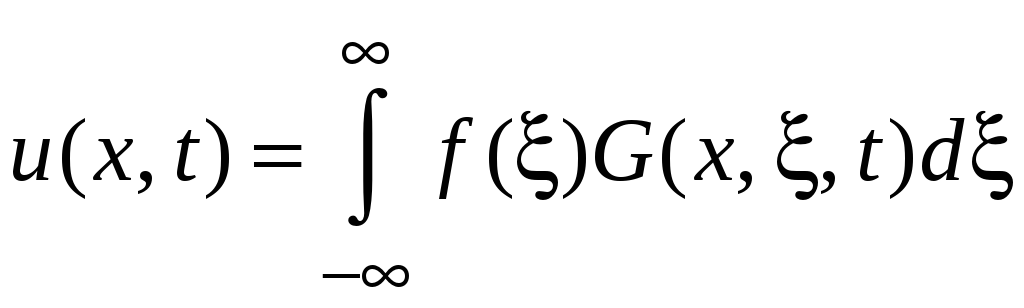, (20)

где 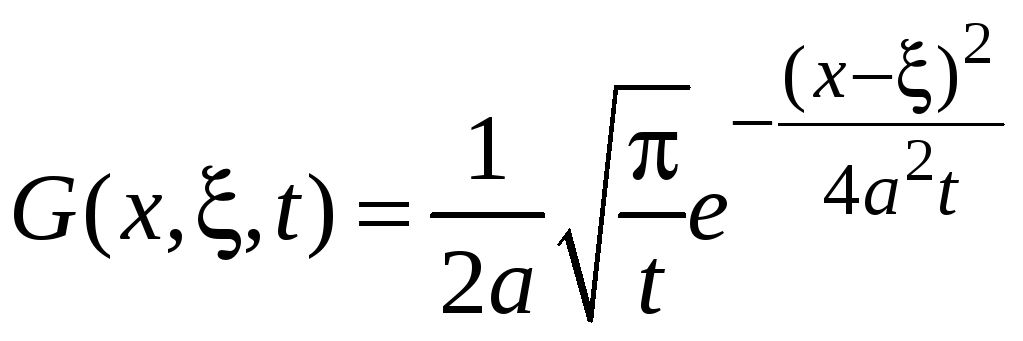есть некоторое ядро интегрального представления, причем это ядро не зависит от начальных условий задачи.

Функцию , саму являющуюся решением уравнения (12), называют фундаментальным решением или функцией Грина уравнения теплопроводности в бесконечном стержне.

Математически она позволяет найти решение уравнения теплопроводности с любыми начальными условиями в виде (20). Но эта функция имеет и важный физический смысл, который мы сейчас и рассмотрим.

Пусть начальное распределение температуры в стержне таково:

. (21)

Здесь – дельта-функция Дирака, наиболее распространенный в приложениях пример сингулярной обобщенной функции, определяемой следующим образом: для любой непрерывной на всей вещественной оси функции

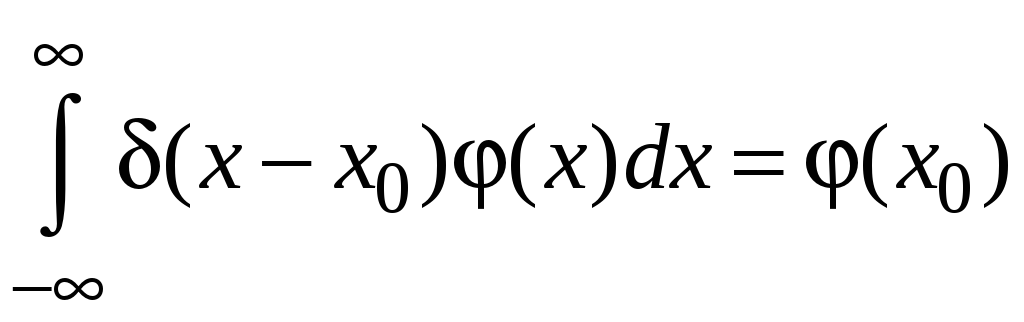. (22)

Физически условия (21) означает, что в точке в начальный момент в стержень введено единичное количество тепла.

В соответствии с общей схемой решения и с учетом определения (22) -функции

,

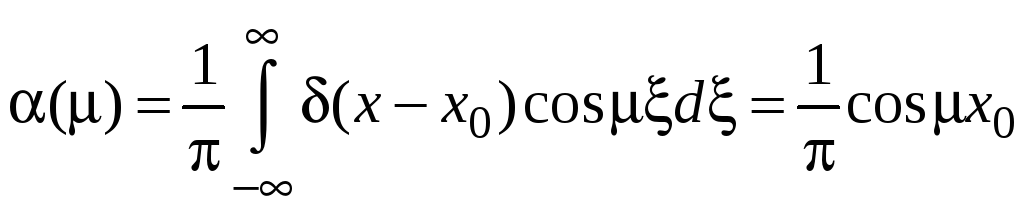и решение уравнения (12) с начальным условием (21) будет иметь вид

.

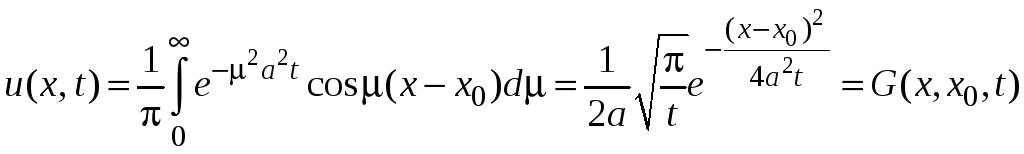Таким образом, фундаментальное решение или функция Грина представляет собой решение задачи о распространении тепла в бесконечном стержне от точечного теплового импульса сообщенного стержню в точке в начальный момент времени.

Теперь физический смысл формулы (20) можно пояснить следующим образом: начальное распределение температуры можно представить как бесконечную последовательность тепловых единичных импульсов с множителями . Каждый отдельный импульс при дает распределение температуры в стержне вида 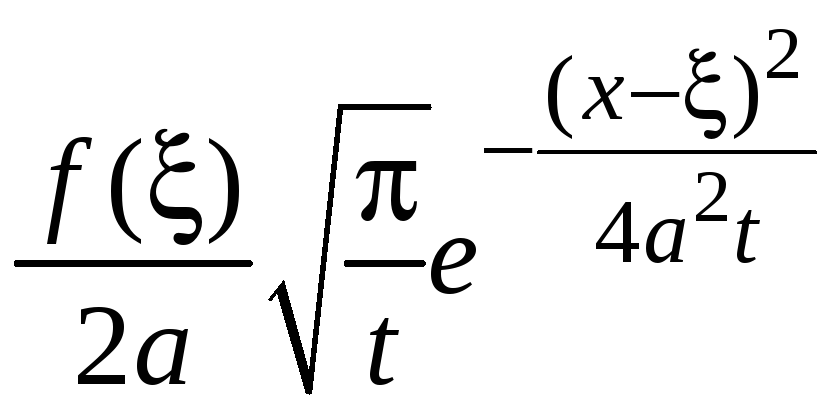, а их сумма, точнее интеграл (20) есть результирующее распределение температуры в каждой точке стержня в любой момент времени.

Решение задачи (12 – 13) может быть получено достаточно просто, если постоянна на некотором отрезке стержня и равна нулю вне его.

Уравнение гиперболического типа

описывает, как правило, процессы колебательного характера, например, колебания струны или продольные колебания тонкого упругого стержня.

При описании колебаний струны это поперечное отклонение точки струны с координатой в момент времени . При продольных колебаниях упругого стержня – продольное смещение сечения, имеющего координату для стержня в состоянии покоя.

Закрепленным концам струны или стержня соответствуют условия или . В упругом стержне продольные напряжения пропорциональны , поэтому условие на том или другом торце стержня означает, что этот торец свободен.

В гиперболическим уравнении производная по времени имеет второй порядок в отличии от параболического уравнения, и по этой причине должны быть заданы два начальных условия:

и .

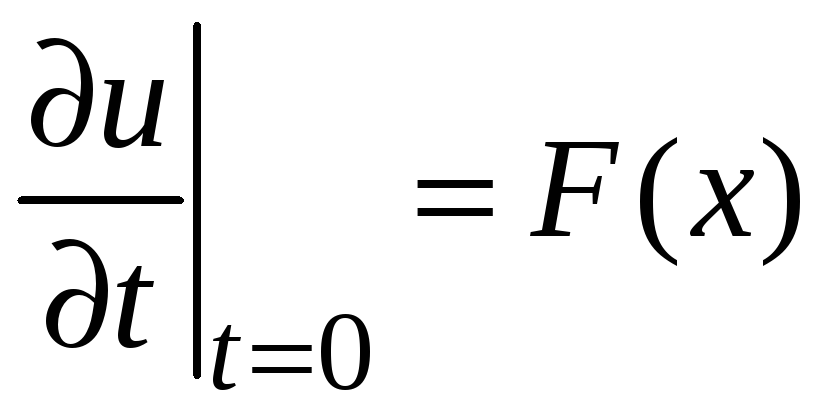Рассмотрим метод Фурье разделения переменных для гиперболического уравнения на следующем примере.

Пример. Решить уравнение

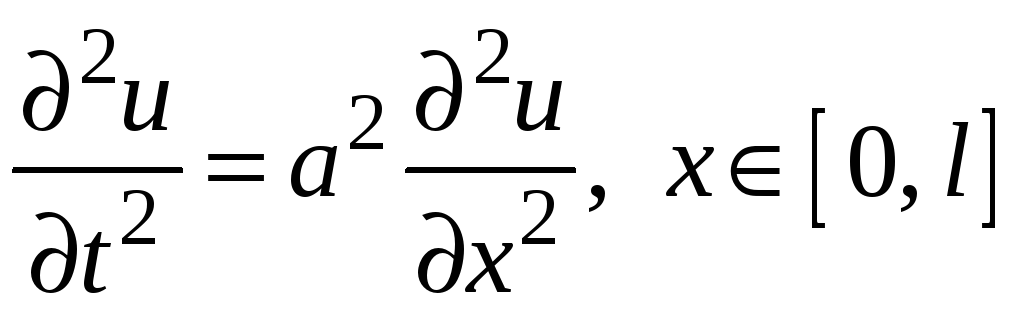, (1)

если

, (2)

, (3)

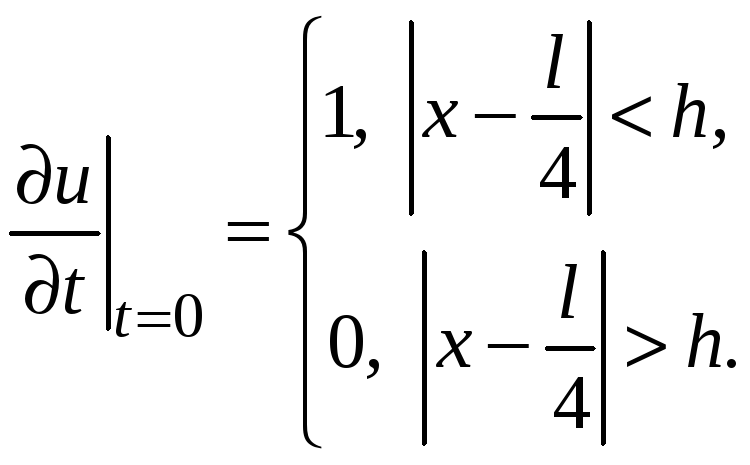(4)

Решение. Эта задача описывает, например, колебания струны, закрепленной на концах, начальные отклонения которой равны нулю, но участок струны шириной в окрестности точки с координатой получает в поперечном направлении начальную скорость, равную 1. Эта ситуация реализуется, в частности, в рояле, когда при нажатии клавиши плоский молоточек ударяет по струне в некоторой точке.

Применяя метод Фурье разделения переменных снова получаем два обыкновенных дифференциальных уравнения, только уравнение для оказывается уравнением второго порядка

. (5)

Для функции получаем аналогичную задачу Штурма-Лиувилля

, (6)

. (7)

Значение не является собственным, так как соответствующая функция . Если же , то

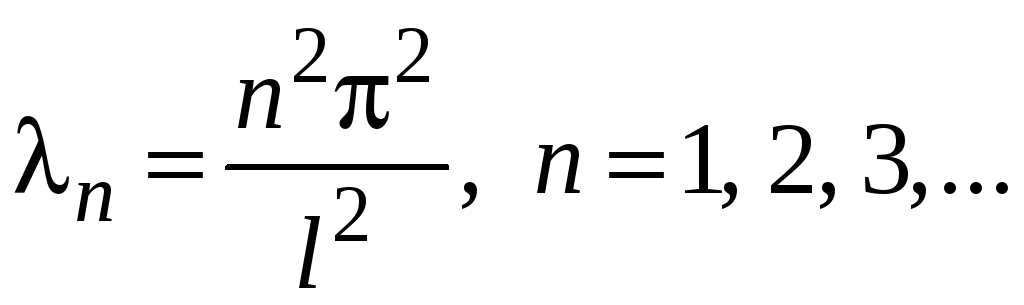
и собственные функции , квадрат нормы которых равен для всех .

Теперь обратимся к уравнению (5) для . Каждому собственному значению будет соответствовать решение уравнения