
2 семестр МПиТК / 2-й семестр / Лекции Соколова / 2_8
.docНеявные функции.
Рассмотрим сначала уравнение, связывающее
две переменные![]() .
Здесь может получиться все, что угодно.
.
Здесь может получиться все, что угодно.
Нас интересует вопрос, когда это уравнение
задает
![]() как
функцию от
как
функцию от
![]() .
.
Теорема 1. Пусть задана
![]() ,
точка
,
точка
![]() такая, что
такая, что
![]() .
И функция
.
И функция![]() определена,
непрерывна и имеет непрерывные частные
производные первого порядка в некоторой
окрестности
определена,
непрерывна и имеет непрерывные частные
производные первого порядка в некоторой
окрестности
![]() .
При этом
.
При этом
![]() на
на
![]() .
Тогда если мы рассмотрим множество
.
Тогда если мы рассмотрим множество
![]() ,
то
,
то
Для любого прямоугольника
![]() ,
число
,
число
![]() можно
уменьшить таким образом, что на пересечении
можно
уменьшить таким образом, что на пересечении
![]() ,
где
,
где![]() ,
,
![]() выражается
однозначно через
выражается
однозначно через
![]() ,
то есть
,
то есть
![]() ,
которая непрерывно дифференцируема на
,
которая непрерывно дифференцируема на
![]() .
.
Замечание: мы требовали, чтобы
![]() на
всей
на
всей
![]() ,
в силу непрерывной дифференцируемости
достаточно потребовать, чтобы
,
в силу непрерывной дифференцируемости
достаточно потребовать, чтобы
![]() в
самой точке
в
самой точке
![]() .
.
Пояснение:
Допустим у нас есть окружность![]()
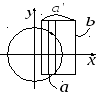
Доказательство:
У нас
![]() ,
пусть для определенности
,
пусть для определенности
![]() .
Зафиксируем
.
Зафиксируем
![]() ,
тогда рассмотрим функцию
,
тогда рассмотрим функцию
![]() .
.
Получим
![]() ,
значит
,
значит
![]() .
Значит функция в этой точке является
возрастающей, и вообще она возрастает
везде на промежутке
.
Значит функция в этой точке является
возрастающей, и вообще она возрастает
везде на промежутке
![]() .
Значит
.
Значит
![]() при
при
![]()
![]() при
при
![]() .
Наша задача состоит в том, чтобы по
произвольному
.
Наша задача состоит в том, чтобы по
произвольному
![]() найти
единственный
найти
единственный![]() .
.
Зафиксируем
![]() .
.
Найдем
![]() такое, что
такое, что
![]() .
.
![]() .
Исходя из полученных неравенств и того,
что функция
.
Исходя из полученных неравенств и того,
что функция
![]() у
нас непрерывна, значит найдется целая
окрестность, где она меньше нуля,
получаем, что
у
нас непрерывна, значит найдется целая
окрестность, где она меньше нуля,
получаем, что
![]() при
при
![]() .
.
![]() при
при
![]() .
.
С одной стороны она больше нуля, с другой меньше, тогда по непрерывности
![]() .
.
Если задана функция
f
(x,y)
и мы
рассматриваем множество точек
![]() ,
что f(x,y)
= 0, и в
некоторой окрестности точки
,
что f(x,y)
= 0, и в
некоторой окрестности точки
![]() f
(x,y)
непрерывно дифференцируема, и
f
(x,y)
непрерывно дифференцируема, и
![]() во всей окрестности, тогда для любого
прямоугольника
во всей окрестности, тогда для любого
прямоугольника
![]() ,
такой что его замыкание
,
такой что его замыкание
![]() , то число
, то число
![]() можно уменьшить таким образом, что если
мы возьмем новый прямоугольник
можно уменьшить таким образом, что если
мы возьмем новый прямоугольник
![]() ,
множество
,
множество
![]() задается уравнением
задается уравнением
![]() ,
где
,
где
![]() и
и
![]() является непрерывно дифференцируемой
на промежутке
является непрерывно дифференцируемой
на промежутке
![]() .
Мы доказали, что y
выражается через х:
мы уменьшили окрестность и для любого
x
нашли соответствующий y,
такой что (x,y)
принадлежит
множеству
.
Мы доказали, что y
выражается через х:
мы уменьшили окрестность и для любого
x
нашли соответствующий y,
такой что (x,y)
принадлежит
множеству
![]() ,
т.е.
,
т.е.
![]() .
Докажем, что полученная функция
.
Докажем, что полученная функция
![]() будет непрерывно дифференцируема и
вычислим ее производную.
будет непрерывно дифференцируема и
вычислим ее производную.
Зададим приращения
![]() точке
точке
![]() ,
такие что
,
такие что
![]() ,
тогда распишем приращение функции:
,
тогда распишем приращение функции:
![]() ,
причем в промежуточной точке
,
причем в промежуточной точке
![]()
![]() - одно и то же, т.к. у нас в формуле Тейлора
для функции n
– переменных
- одно и то же, т.к. у нас в формуле Тейлора
для функции n
– переменных
![]() .
Заметим, что у нас
.
Заметим, что у нас
![]() ,
т.к. обе эти точки принадлежат по условию
множеству
,
т.к. обе эти точки принадлежат по условию
множеству
![]() .
Тогда
.
Тогда
 .
.
Устремим
![]() к нулю, тогда, т.к. по условию частные
производные непрерывны, при
к нулю, тогда, т.к. по условию частные
производные непрерывны, при
![]()
![]() .
Нам нужно теперь доказать, что из того,
что
.
Нам нужно теперь доказать, что из того,
что
![]() следует, что
следует, что
![]() тоже стремится к нулю. Т.е. фактически
нужно доказать, что функция
тоже стремится к нулю. Т.е. фактически
нужно доказать, что функция
![]() является непрерывной. Выразим из
полученного равенства
является непрерывной. Выразим из
полученного равенства
![]() :
:
 .
.
Производная
![]() непрерывна на
непрерывна на
![]() (вот здесь нам нужно, что прямоугольник
содержится в
(вот здесь нам нужно, что прямоугольник
содержится в
![]() вместе с своим замыканием, потому что
когда мы говорим об ограниченности
непрерывной функции, нам нужно замкнутое
множество), значит она является
ограниченной на этом множестве:
вместе с своим замыканием, потому что
когда мы говорим об ограниченности
непрерывной функции, нам нужно замкнутое
множество), значит она является
ограниченной на этом множестве:
![]() .
.
![]() и также непрерывна на
и также непрерывна на
![]() ,
значит она достигает своего локального
минимума, причем этот
,
значит она достигает своего локального
минимума, причем этот
![]() ,
,
![]() .
Значит
.
Значит
![]() ,
а из этого следует, что при
,
а из этого следует, что при
![]() .
Теперь мы можем устремить
.
Теперь мы можем устремить
![]() к нулю, тогда получим:
к нулю, тогда получим:
 .
.
Дифференцируемость
функции
![]() доказана. Еще разговор шел о непрерывной
дифференцируемости. Т.к. у нас обе функции
доказана. Еще разговор шел о непрерывной
дифференцируемости. Т.к. у нас обе функции
![]() и
и
![]() непрерывны и
непрерывны и
![]() , то и функция
, то и функция
![]() является непрерывной.
является непрерывной.
Теорема доказана.
П ример:
ример:
Рассмотрим в
качестве примера функцию
![]() ,
,
![]() - окружность в плоскости xy,
она и будет составлять множество
- окружность в плоскости xy,
она и будет составлять множество
![]() .
Выделим двумерную окрестность
.
Выделим двумерную окрестность
![]() точки
точки
![]() так, чтобы для всех точек в этой окрестности
так, чтобы для всех точек в этой окрестности
![]() (окрестность, обозначенная на рисунке
пунктирной линией не может быть взята
в качестве
(окрестность, обозначенная на рисунке
пунктирной линией не может быть взята
в качестве
![]() ,
т.к. в точках
,
т.к. в точках
![]() (они отмечены на рисунке) производная
(они отмечены на рисунке) производная
![]() ).
В качестве начального прямоугольника
берем прямоугольник, который полностью
содержится в
).
В качестве начального прямоугольника
берем прямоугольник, который полностью
содержится в
![]() ,
вместе со своим замыканием.
,
вместе со своим замыканием.
В замечании мы
говорили, что неравенство нулю
![]() на всей окрестности
на всей окрестности
![]() можно заменить на
можно заменить на
![]() вследствие ее непрерывности, но тогда
придется немного изменить условие
теоремы: нужно было бы уменьшать не
только a,
но и b,
т.к. теперь мы можем утверждать, что
существует некоторая окрестность точки
вследствие ее непрерывности, но тогда
придется немного изменить условие
теоремы: нужно было бы уменьшать не
только a,
но и b,
т.к. теперь мы можем утверждать, что
существует некоторая окрестность точки
![]() ,
в которой
,
в которой
![]() ,
а окрестность мы берем не только по x,
но и по y.
Если же мы возьмем в качестве
,
а окрестность мы берем не только по x,
но и по y.
Если же мы возьмем в качестве
![]() точку, обозначенную на рисунке
точку, обозначенную на рисунке
![]() ,
в которой
,
в которой
![]() ,
то для нее мы совсем ничего не можем
сказать, потому что мы не сможем найти
такую окрестность этой точки, в которой
функция
,
то для нее мы совсем ничего не можем
сказать, потому что мы не сможем найти
такую окрестность этой точки, в которой
функция
![]() выражается через х
однозначно.
выражается через х
однозначно.
Обобщим доказанную теорему.
Теорема2:
Звучит почти так
же, как теорема 1, только точка
![]() - пространственная.
- пространственная.
Пусть задана
функция
![]() ,
т.е.
,
т.е.
![]() - непрерывно дифференцируемая,
- непрерывно дифференцируемая,
![]() .
.
![]() - множество таких точек, что
- множество таких точек, что
![]() .
Предположим,
что в некоторой окрестности
.
Предположим,
что в некоторой окрестности
![]() ,
где
,
где
![]() ,
,
![]() функция
функция
![]() непрерывно дифференцируема и
непрерывно дифференцируема и
![]() ,в
этой окрестности тогда каков
бы ни был
,в
этой окрестности тогда каков
бы ни был
![]() - мерный прямоугольник
- мерный прямоугольник
![]() , такой что
, такой что
![]() ,
число
,
число
![]() можно уменьшить таким образом, что
можно уменьшить таким образом, что
![]() и множество
и множество
![]() ,
причем функция
,
причем функция
![]() - непрерывная дифференцируемая функция
многих переменных и
- непрерывная дифференцируемая функция
многих переменных и
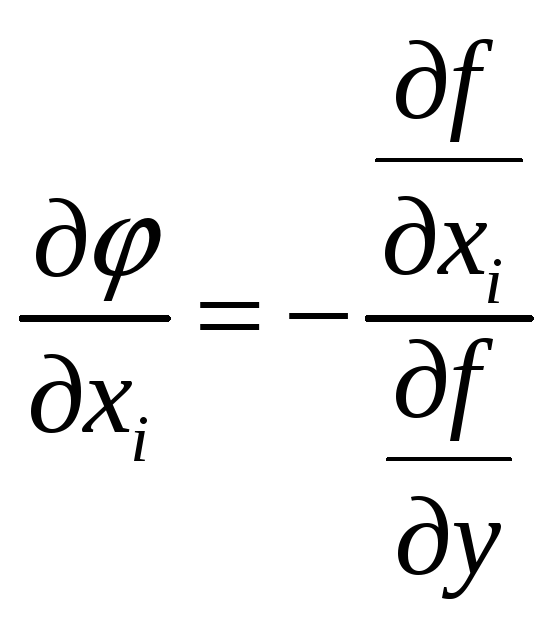 .
.
Все точно так же,
только над x
появится черточка и
![]() .
.
Теорема3:
Пусть заданы
функции
![]() ,
где
,
где
![]() ,
,
![]() ,
i
меняется в пределах:
,
i
меняется в пределах:
![]() .
Тогда множество
.
Тогда множество
![]() .
Берем точку
.
Берем точку
![]() ,
говорим, что в некоторой окрестности
этой точки
,
говорим, что в некоторой окрестности
этой точки
![]() частных производных (у нас m
функций и m
переменных, ранее мы накладывали условие
только на y)
мы завяжем в следующее условие. Составим
Якобиант (определитель матрицы Якоби):
частных производных (у нас m
функций и m
переменных, ранее мы накладывали условие
только на y)
мы завяжем в следующее условие. Составим
Якобиант (определитель матрицы Якоби):
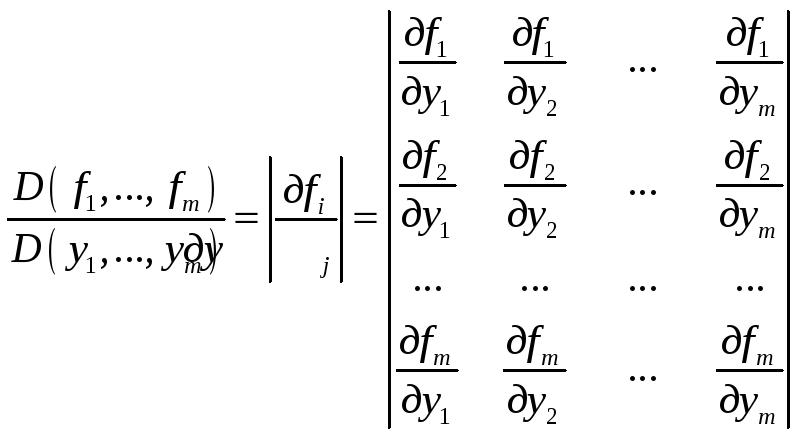 .
Если
.
Если
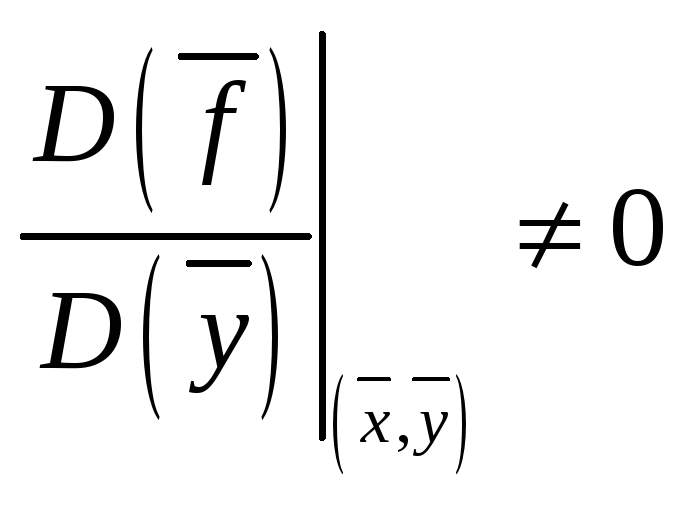 ,
где
,
где
![]() ,
то каков бы ни был прямоугольник
,
то каков бы ни был прямоугольник
![]() ,
,
![]() ,
числа
,
числа
![]() можно уменьшить таким образом, что для
прямоугольника
можно уменьшить таким образом, что для
прямоугольника
![]() ,
множество
,
множество
![]() задается уравнениями:
задается уравнениями:
![]() ,
причем
,
причем
![]() имеют непрерывные частные производные.
имеют непрерывные частные производные.
Пример:
n = 1, m = 2;
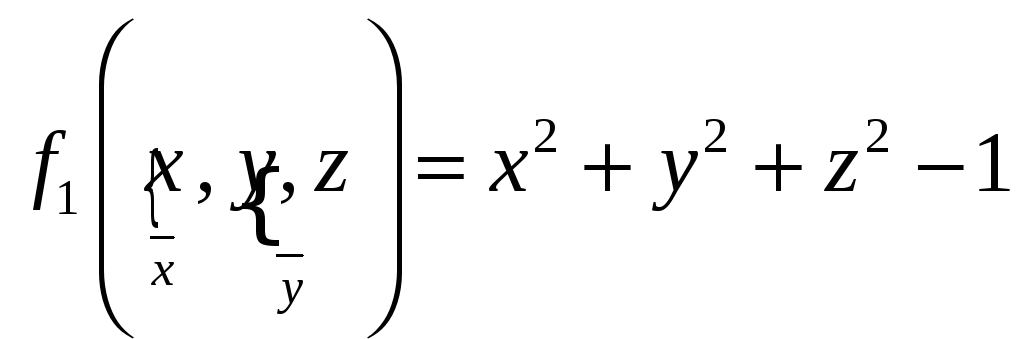 ,
,
![]() ,
,
![]() - сечение шара плоскостью.
- сечение шара плоскостью.
Приведенные уравнения называются уравнениями связи.
Обе функции полностью удовлетворяют условию теоремы 3.
Составим якобиан:
![]() ,
т.е. теорема справедлива в окрестности
любой точки
,
т.е. теорема справедлива в окрестности
любой точки
![]() ,
тогда
,
тогда
y и z выразятся однозначно через х.
Найдем частные
производные
![]() :
:
![]()
Эти уравнения называются дифференциальными уравнениями связи.
![]()
Из условия
![]() (мы
по условию рассматриваем только такие
точки)
(мы
по условию рассматриваем только такие
точки)
![]() .
.
Гладкая поверхность. Касательная плоскость.
Рассмотрим сначала
случай, когда множество задается явно:
![]() ,
где
,
где
![]() .
А
– открытое множество. Если функция
имеет непрерывные
.
А
– открытое множество. Если функция
имеет непрерывные
![]() и
и
![]() на множестве А,
то множество точек
на множестве А,
то множество точек
![]() ,
,
![]() задает гладкую
поверхность.
задает гладкую
поверхность.
Теперь рассмотрим
функцию, заданную неявно. Пусть у нас
есть функция
![]() и уравнение
и уравнение
![]() .
По всему сказанному выше, если у нас
.
По всему сказанному выше, если у нас
![]() ,
то z
можно выразить через х
и
y,
но может случиться так, что
,
то z
можно выразить через х
и
y,
но может случиться так, что
![]() ,
но
,
но
![]() ,
тогда можно выразить y.
Тогда общее условие
запишем в следующем виде. Пусть f
имеет
непрерывные частные производные
,
тогда можно выразить y.
Тогда общее условие
запишем в следующем виде. Пусть f
имеет
непрерывные частные производные
![]() , все они непрерывны на
, все они непрерывны на
![]() и
и
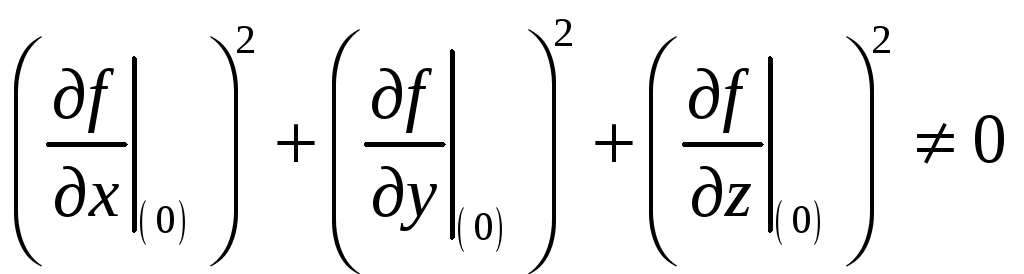 ,
т.е. все частные производные не обращаются
в ноль одновременно. Тогда в окрестности
этой точки функция задает гладкую
поверхность.
,
т.е. все частные производные не обращаются
в ноль одновременно. Тогда в окрестности
этой точки функция задает гладкую
поверхность.
Построим касательную плоскость к этой поверхности.
Пусть у нас есть
поверхность
![]() ,
задаваемая уравнением
,
задаваемая уравнением
![]() ,
точка
,
точка
![]() ,
такая что
,
такая что
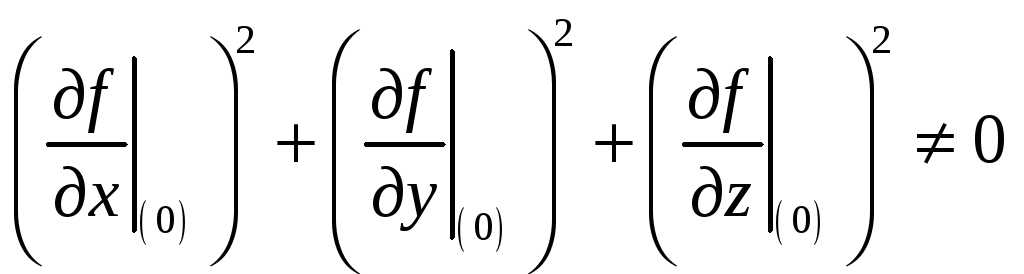 ,
тогда это равенство выполняется и в
некоторой окрестности точки
,
тогда это равенство выполняется и в
некоторой окрестности точки
![]() ,
т.к. частные производные у нас непрерывны.
Тогда в этой окрестности полностью
выполняется условие теоремы 1 из
предыдущего пункта для какой-то
переменной. Раз сумма квадратов частных
производных
,
т.к. частные производные у нас непрерывны.
Тогда в этой окрестности полностью
выполняется условие теоремы 1 из
предыдущего пункта для какой-то
переменной. Раз сумма квадратов частных
производных
![]() ,
значит какая-то из этих частных производных
точно
,
значит какая-то из этих частных производных
точно
![]() .
Предположим, что
.
Предположим, что
![]() (далее мы покажем, что на самом деле все
равно, какая из частных производных
(далее мы покажем, что на самом деле все
равно, какая из частных производных
![]() ).
Тогда в окрестности этой точки у нас
получится явное выражение: поверхность
).
Тогда в окрестности этой точки у нас
получится явное выражение: поверхность
![]() будет задаваться уравнением
будет задаваться уравнением
![]() (по Теореме
1). Запишем
уравнение касательной плоскости, которое
для явно заданных функций мы уже выводили:
(по Теореме
1). Запишем
уравнение касательной плоскости, которое
для явно заданных функций мы уже выводили:
![]() .
.
Теперь по той же
теореме:
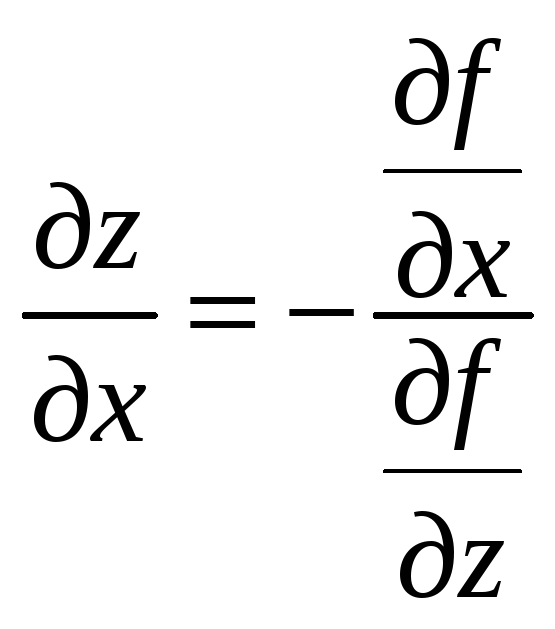 ,
,
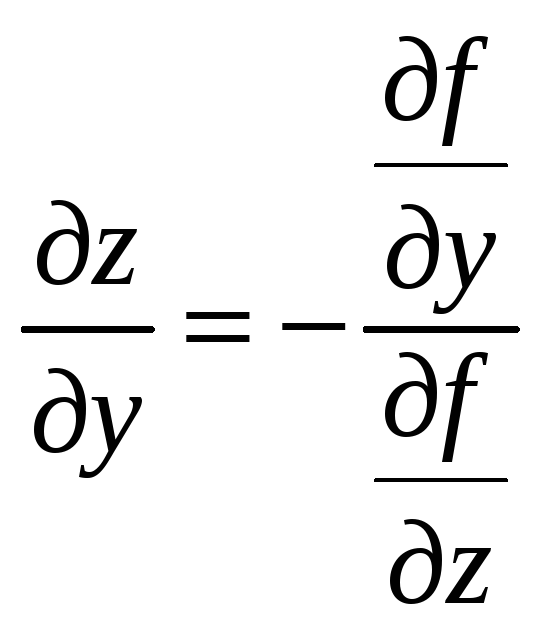 .
Тогда подставив эти выражение в формулу
для касательной плоскости, получим:
.
Тогда подставив эти выражение в формулу
для касательной плоскости, получим:
![]() .
Тогда
.
Тогда
![]() .
Т.е. получили, что градиент перпендикулярен
касательной плоскости.
.
Т.е. получили, что градиент перпендикулярен
касательной плоскости.
Пример:
Построим касательную
плоскость к поверхности
![]() (шару) в точке
(шару) в точке
![]() .
.
![]() в этой точке = 0. Однако заметим, что если
бы при выводе уравнения касательной
плоскости у нас не
в этой точке = 0. Однако заметим, что если
бы при выводе уравнения касательной
плоскости у нас не
![]() ,
а
,
а
![]() или
или
![]() ,
то конечная формула бы не изменилась.
Итак, воспользуемся уже полученной
формулой:
,
то конечная формула бы не изменилась.
Итак, воспользуемся уже полученной
формулой:
![]() ,
,
![]() ,
получаем, что
,
получаем, что
![]()
![]() - касательная
плоскость.
- касательная
плоскость.
