Применительно к задачам о наименьших квадратах [править]

На практике часто встречаются задачи, в которых требуется произвести настройку свободных параметров объекта или подогнать математическую модель под реальные данные. В этих случаях появляются задачи о наименьших квадратах:

Эти задачи отличаются особым видом градиента и матрицы Гессе:

где  — матрица Якоби вектор-функции ,  — матрица Гессе для её компоненты .

Тогда очередное направление  определяется из системы:

Геометрическая интерпретация 

Основная идея метода заключается в следующем: задаётся начальное приближение вблизи предположительного корня, после чего строится касательная к исследуемой функции в точке приближения, для которой находится пересечение с осью абсцисс. Эта точка и берётся в качестве следующего приближения. И так далее, пока не будет достигнута необходимая точность.

Пусть  — определённая на отрезке  и дифференцируемая на нём вещественнозначная функция. Тогда формула итеративного исчисления приближений может быть выведена следующим образом:

где  — угол наклона касательной в точке .

Следовательно искомое выражение для  имеет вид:

Итерационный процесс начинается с некоего начального приближения  (чем ближе к корню, тем лучше, но если предположения о его нахождении отсутствуют, методом проб и ошибок можно сузить область возможных значений, применив теорему о промежуточных значениях).

Алгоритм 

1. Задается начальное приближение .

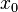2. Пока не выполнено условие остановки, в качестве которого можно взять  или  (то есть погрешность в нужных пределах), вычисляют новое приближение: .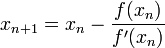

Метод наискорейшего спуска

Рис.3 Геометрическая интерпретация метода наискорейшего спуска. На каждом шаге выбирается так, чтобы следующая итерация была точкой минимума функции  на луче L.

Этот вариант градиентного метода основывается на выборе шага из следующего соображения. Из точки  будем двигаться в направлении антиградиента до тех пор пока не достигнем минимума функции f на этом направлении, т. е. на луче:

.

Другими словами,  выбирается так, чтобы следующая итерация была точкой минимума функции f на луче L (см. рис. 3). Такой вариант градиентного метода называется методом наискорейшего спуска. Заметим, кстати, что в этом методе направления соседних шагов ортогональны.

Метод наискорейшего спуска требует решения на каждом шаге задачи одномерной оптимизации. Практика показывает, что этот метод часто требует меньшего числа операций, чем градиентный метод с постоянным шагом.

В общей ситуации, тем не менее, теоретическая скорость сходимости метода наискорейшего спуска не выше скорости сходимости градиентного метода с постоянным (оптимальным) шагом.

значимыми. Это означает, что достигнута область оптимума.

Пример:

Дана система лин. Уравнений

Зх1-5x2+x3+2x4 =1

2x1-2x2 +x4-x5=-4

X1-3x2-2x4-x5=-5

Ф=х1+2х2+х3+х4+х5

Требуется среди неотрицательных решений данной системы выбрать такое, которое минимизирует данную целевую функцию f.

Прежде всего замечаем, что переменная x3 входит только в первое уравнение системы и коэффициент при x3 имеет тот же знак, что и свободный член этого уравнения.

Поэтому разрешим это уравнение относительно x3

X3=1-(3x1-5x2+2x4)

Примем x3 одним из базисных неизвестных. Для остальных двух уравнений вводим искусственные переменные (неизвестные(у1 и у2). В результате:

x3=1-(3x1-5x2+2x4)

Y1=4-(-2x4+2x2-x4+x5)

Y2=5-(-x1+3x2-2x4+x5)

С помощью симплекс-метода минимизируем следующую функцию:

Ф=у1+у2=9-(-3х1+5х2+3х4+2х5)

Первая Симплекс-таблица имеет вид:

							*****
	Базисные	Свободные	Х1	Х2	Х3	Х4	Х5	У1	У2
	Х3	1	3	-5	1	2	0	0	0
*****	У1	4	-2	2	0	-1	1	1	0
	У2	5	-1	3	0	-2	1	0	1
	Ф'	9	-3	5	0	-3	2	0	0
	Ф	0	-1	-2	0	0	0	0	0

Последующие шаги имеет целью минимизацию Ф''. Целевая функция при этом преобразовании играет пассивную роль. Разрешающий элемент «1» выбираем в строке «у», и столбце «х5».

Таким образом, в результате первого шага неизвестное «у» выходит из базиса. Далее, поскольку столбцы «у1» и «у2» должны вычеркиваться на последнем шаге (после достижения минимума «Ф»), то столбец «у1» имеет смысл вычеркивать уже сейчас. Переходим к таблице 2.

			*****	*****
	Базисные	Свободные	Х1	Х2	Х3	Х4	Х5	У2
*****	Х3	1	3	-5	1	2	0	0
	Х5	4	-2	2	0	-1	1	0
*****	У2	1	1	1	0	-1	0	1
	Ф'	1	1	1	0	-1	0	0
	Ф	0	1	-2	0	0	0	0

Таким образом, после второго шага оба искуственных неизвестных выходят из системы и становятся небазисными.

Этот факт уже свидетельствует о достижении минимума

minФ’=0

Так как в последнем базисном решении F=y1+y2

Отбрасываем столбец «у2» и строку «Ф» и переходим к следующей таблице 3.

		*****
Базисные	Свободные	Х1	Х2	Х3	Х4	Х5
Х1	6/8	1	0	1/8	-3/8	0
Х5	5	0	0	½	-1/2	1
Х2	2/8	0	1	-1/8	-5/8	0
Ф	10/8	0	0	-1/8	-13/8	0

Как видно, целевая функция Ф достигла минимума равного 10/8.

Оптимальное решение есть:

Х1=6/8; х5=5; х2=2/8; х3=х4=0.