7. Бесконечно малые и бесконечно большие функции.

Опр. Функция f(x) наз.бесконечно малой при х →х_0, если

ибесконечно большой при х →х₀ , если

Справедливы теоремы. 1.Сумма и произведение двух бесконечно малых функций (при х →х₀) снова являются бесконечно малыми функциями (при х →х₀).

2.Произведение бесконечно малой функции на ограниченную есть снова бесконечно малая функция.

8. Свойства предела функции.

1. Функция f(x) в точке х₀ может иметь только один предел.

Доказательство: Пусть (1)

и одновременно

где a≠b. (2)

Тогда для любой последовательности { х_n} сходящейся к х₀ (где все х_n≠ х₀), мы должны иметь два предела

что невозможно, т.к. последовательность {f(х_n)} может иметь только один предел.

2.Если f(x) имеет предел в точке, то в некоторой окрестности этой точки функция ограничена.

Доказательство. Предположим, что это не так. U₁=( х₀-ε ; х₀+ε), ε>0 . Ввиду неограниченности f(x) в этой окрестности должна найтись точка х₁ U₁ , такая что │f(х₁)│>1. Уменьшим вдвое эту окрестность и рассмотрим U₂=( х₀-ε/2 ; х₀+ε/2), ε>0 окрестность, в ней снова найдется такая точка х₂ U₂ , такая что │f(х₂)│>2. Продолжив это рассуждение, получим U_n=( х₀-ε/n ; х₀+ε/n) , f(х_n) > n, х_n → х₀ ; f(х_n)→∞. мы пришли к противоречию.

3.Если для всех точек х некоторой окрестности точки х₀ выполняется неравенство f(x) ≥b , то и если такой предел существует. (доказывается по соответствующему свойству предела числовой последовательности).

4.Если в некоторой окрестности точки х₀ имеем f(x)≥g(x) , то и если пределы существуют.

5. Если в некоторой окрестности точки х₀ имеем f(x)≥g(x)≥h(x) причем пределы f(x) и h(x) при х→ х₀ существуют и равны между собой

Арифметические свойства пределов.

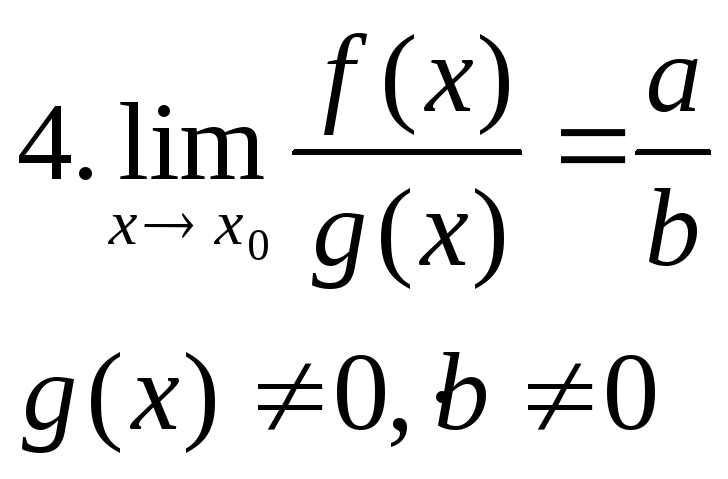
9. Односторонние пределы.

Опр.Число а называют пределом функцииf(x)в точке х₀ справа, если для любой сходящейся к х₀ последовательности {х_n}, в которой все х_n>х₀, соответствующая последовательность {f(х_n)} сходится к а.

Аналогично определяют предел функции слева:

10. Асимптоты функций.

Прямая у=а называется вертикальной асимптотой графика у=f(x) , если хотя бы один из пределов

Прямая у=кх+b является наклонной асимптотой графика у=f(x) при х→+∞, если f(x) представима в виде f(x)= кх+b+α(х), где

Теорема. Для того чтобы график функции у=f(x) имел х→+∞ наклонную асимптоту , необходимо и достаточно, чтобы существовали два предела

Аналогично определяется наклонная асимптота для случая х→-∞.

11 Монотонные функции.

Функция y=f(x) называется возрастающей (убывающей) на некотором множестве Х принадл. R¹, если она определена на этом множестве и если для любых значений х1, х2, принадлежащим Х, из условия х1<х2 следует нер-во:

f(x1)<f(x2) (f(x1) >f(x2))

Функция y=f(x) называется неубывающей (невозрастающей) на некотором множестве Х принадл. R¹, если она определена на этом множестве и если для любых значений х1, х2 принадлежащим Х из условия х1<х2 следует нер-во:

f(x1)≤f(x2) (f(x1) ≥f(x2))

Невозрастающие, неубывающие, возрастающие и убывающие ф-и наз. Монотонными.

Любая ограниченная монотонная функция имеет предел.

12. Замечательные пределы.

1. lim f(x)sinx/x =1(при х→0) – первый замечательный предел.

Док-во. Т.к. ф-я y= sinx – четная, то достаточно показать, что предел при х→0 справа равен 1.

T

M

tgx

x

K A

O

MK= sinx Видно, что sinx<x<tgx,

1<x/ sinx<1/cosx

1>sinx/x>cosx

при х→0 справа имеем lim cosx=1, lim 1=1. Значит получили требуемое равенство.

2) lim (1+1/x)^x =e(х→+ (-)∞) – второй замечательный предел.

Док-во.

Докажем

1)при +∞. Пусть х – любое число. Найдем такое целое n, чтобы выполнялось нер-во:

n ≤ x< n+1 (1)

Будем считать, что х>1,n>0. Сделав необходимые преобразования, получим: 1+1/ n ≥ 1+1/x> 1+1/(n+1)

Зная условие (1), можем получить: (1+1/ n)ⁿ⁺¹≥ (1+1/x)^x> (1+1/(n+1))ⁿ или f(x) ≥(1+1/x)^x>g(x). При х→+∞ ,n →+∞, f(x) и g(x)→е. По св- ву предела ф-и lim (1+1/x)^x →е(при х→+∞), что и т.д.

2) при -∞. Пусть х=-t, где t>0.

(1+1/x)^x=(1-1/t)-^t =((t-1)/t)^-t =(t/(t-1))^t =(1+1/(t-1))^t =(1+1/(t-1))^t-1 (1+1/(t-1))^x Выражение в правой части →е*1=е при х→-∞, т.е. t →+∞, что и т.д.