complan_taskbook_1

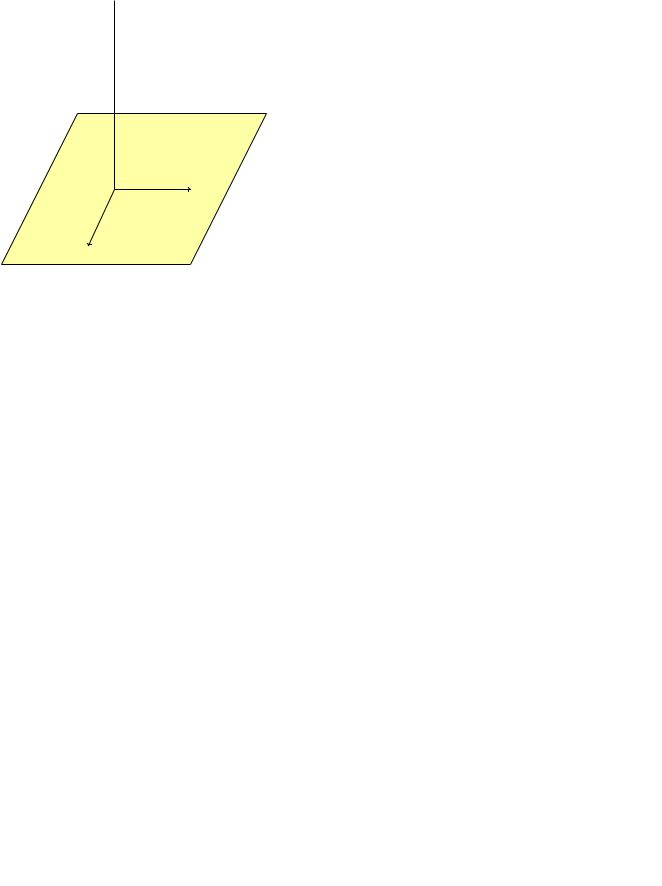
Роздiл 2. Способи зображення комплексних чисел

11

перетину цiєї прямої зi сферою. Вiдображення z $ M(z) є взаємно однозначним вiдображенням мiж комлексною площиною i сферою, проколотою в точцi N:

N

M(z)

Oiy

x

z

Рис. 3: Сфера Рiмана

Доповнимо комплексну площину символiчною точкою, яка називається нескiнченно вiддаленою точкою, позначимо її 1 i покладемо M(1) = N: Комплексна площина, яка доповнена точкою 1 називається розширеною комплексною площиною або повною комплексною площиною та позначається C, а сфера, на яку вона проектується — сферою Рiмана. Виберемо систему координат ; ; таким чином, щоб осi O i O збiгалися з осями Ox i Oy комплексної площини, а вiсь O була напрямлена вздовж дiаметра сфери Рiмана (див. рис. 3). Координати точки на сферi зв’я- занi рiвнянням 2 + 2 + ( 1=2)2 = 1=4. Зв’язок мiж координатами точки на площинi x, y та координатами точки на сферi, , задається такими формулами

x =

; y =

; =

x

; =

y

; =

jzj2

:

(2.1)

1

1 + jzj2

1 + jzj2

1 + jzj2

1

Матрична iнтерпретацiя комплексних чисел. При операцiях множення та дiлення комплекснi числа мають властивiсть лiнiйних операторiв. А саме, геометрично множення комплексного числа z1 = 1ei'1 на комплексне число z2 = 2ei'2 зводиться до повороту вектора z1 на кут '2 та змiни його довжини в 2 разiв, тобто можна розглядати z1 як вектор, а z2 як лiнiйний оператор, що дiє на цей вектор (або навпаки). Таким чином, кожне комплексне число z = x + iy може бути ототожнено з кососиметричною матрицею другого порядку такого вигляду

z =	y	x	:
	x	y

Для таким матриць виконуються алгебраїчнi операцiї додавання, вiднiмання, множення та дiлення так само, як i для комплексних чисел.

Приклад 2.1. C Зобразити на комплекснiй площинi множину точок

	z + 4i		2
M =	z : Re	z 3	1	:

B

Розв’язання. J Знайдемо множину точок z; яка задовольняє рiвняння

Re zz+ 43i = 12;

c	v. 25 березня 2014 р.
Є. Д. Бiлоколос, Л. Д. Зайцева, Д. Д. Шека, 2014

12

Глава 1. Основнi поняття комплексного аналiзу

це буде межа множини M. Нехай z = x+iy; x; y 2 R: Зауважимо, що z 6= 4i.

Пiдставимо в шукане рiвняння: Re x + iy 3

=

1, або Re

x 3 + iy

=

1

x + iy + 4i

2

x + i(y + 4)

2. Знайдемо частку вiд дiлення двох комплексних чисел, а потiм її дiйсну

частину:

Re (x 3 + iy)(x i(y + 4)) = Re (x 3)x + y(y + 4) + i (yx (x 3)(y + 4)) =

x2 + (y + 4)2

= (x 3)x + y(y + 4) =

x2 + (y + 4)2

1:

x2 + (y + 4)2

2

Розв’яжемо звичайне рiвняння для двох дiйсних змiнних x; y:

(x 3)x + y(y + 4) =

1

;

x2 + (y + 4)2

2

звiдки 2x2 6x + 2y2 + 8y = x2 (y + 4)2, тому 3x2 6x + 3y2 + 16y + 16 = 0:

Отримали рiвняння другого порядку. Видiлимо повнi квадрати:

(x 1)2

8

2

5

2

5

8i

+ y + 3

= 3

;

або

jz z0j = 3;

де z0

= 1 3 :

iy

Це рiвняння описує коло з центром в точцi z0 =

i

1 83i

радiуса

35. Межею множини M буде

ко-

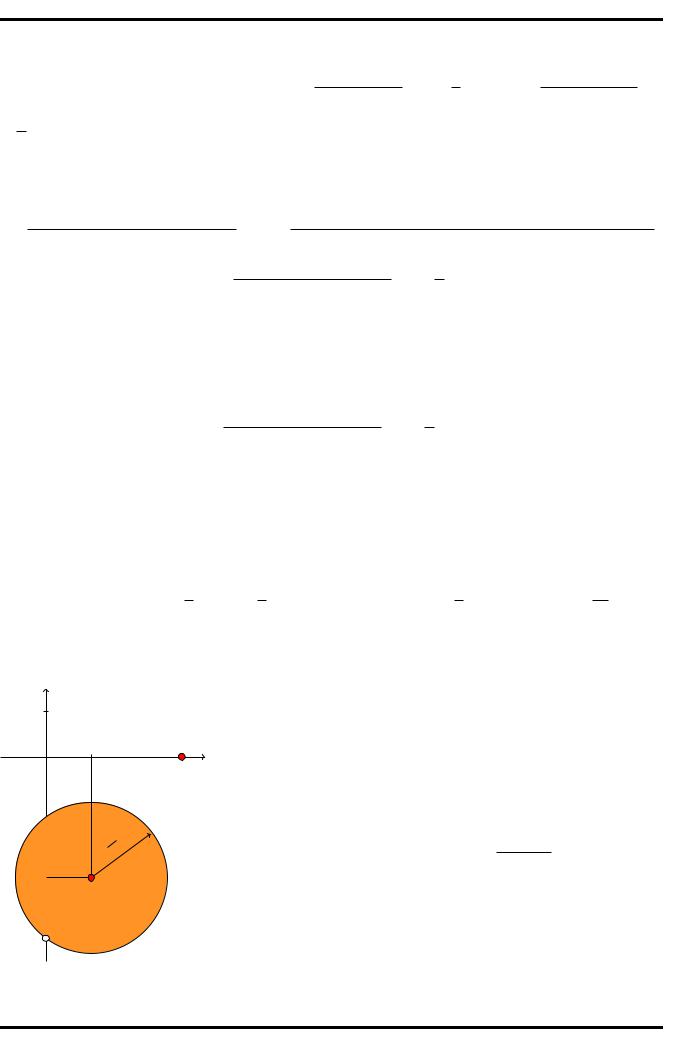
ло з виколотою точкою 4i. Залишилось визна-

1

z1

x

чити,

множина

M — це внутрiшнiсть або зовнi-

шнiсть побудованого кола. Для цього вiзьмемо

довiльну точку комплексної площини, наприклад,

точку z1

= 3. З одного боку, точка z1 не нале-

10

жить множинi M; оскiльки Re z1 3 = 0, тобто її

3

83i

z1 + 4i

z0

координати не задовольняють нерiвнiсть, що ви-

значає M: З iншого боку, точка z1 лежить зовнi

-4i

кола, оскiльки jz1 z0j = 103 . Це означає, що M —

це внутрiшня частина побудованого кола (разом з

Рис. 4: До прикладу 2.1

межею, але з виколотою точкою 4i, див. рис. 4).

Таким чином, M = z : z 1 + 83i 35 nf4ig: I

v. 25 березня 2014 р.

c Є. Д. Бiлоколос, Л. Д. Зайцева, Д. Д. Шека, 2014

Роздiл 2. Способи зображення комплексних чисел

13

Приклад 2.2. C Для заданих z1; z2 2 C зобразити на комплекснiй площинi множину точок M = fz : jjz z1j jz z2jj = 1g : B

Розв’язання. J На вiдмiну вiд попереднього прикладу, тут для розв’язку задачi зручно використати не аналiтичний пiдхiд, а геометричну iнтерпретацiю комплексного числа. Дiйсно, рiвняння jjz z1j jz z2jj = 1 задає множину точок комплексної площини, рiзниця вiдстаней вiд яких до двох фiксованих точок z1 i z2 є величина стала i дорiвнює 1 або 1: З курсу аналiтичної геометрiї вiдомо, що таку властивiсть має крива другого порядку — гiпербола, а точки z1 i z2 — це фокуси даної гiперболи (див. рис. 5). I

iy

z2

x

z1

Рис. 5: До прикладу 2.2

Приклад 2.3. C Який образ на сферi Рiмана має точка i? Точка

1

? B

z

Розв’язання. J Точка i має координати (0; 1); jij

= 1: Для знаходження

координат точки M(i) скористаємось формулами (2.1):

=

0

= 0; =

1

=

1

; =

1

=

1

:

1 + 1

1 + 1 2

1 + 1 2

Таким чином, M(i) =

0;

1

;

1

:

2

2

має координати

=

1

x

y

1

Нехай z = x+iy; z 6= 0: Тодi точка

;

;

z

z

2

z

2

z

1

j j

j j

: З формул (2.1) випливає, що точка M

1

має такi координати:

z

j

z

j

1 =

x=jzj2

=

x

=

; 1 =

y=jzj2

=

y

=

;

1 + (1= z

)2

1 + jzj2

1 + (1= z

)2

1 + jzj2

z

z

z

z

j j

(1=jzj)2

1

j j

1 =

=

= 1

:

1 + (1= z

)2

1 + jzj2

z

z

j j

Таким чином, M

z1 = ( ; ; 1 ) : Якщо z = 0; тодi z1

= 1; M(1) =

N

(пiвнiчний полюс сфери).

I

Приклад 2.4. C При якому значеннi параметра a колу jz ij = a;

a > 0

комплексної площини вiдповiдає велике коло на сферi Рiмана? B

Розв’язання. J Спочатку зауважимо, що jz ij

= a тодi i тiльки тодi, коли

z

2

i

=

a(cos ' + i sin '); '

(

; ]; або z = a cos ' + i(a sin ' + 1): Крiм того,

2

+ 2a sin ':

2

jzj

= 1 + a

Тодi образ точки z (яка лежить на колi jz ij = a) на

сферi Рiмана має такi координати

=

a cos '

;

=

a sin ' + 1

;

=

1 + a2 + 2a sin '

:

2 + a2 + 2a sin '

2 + a2 + 2a sin '

2 + a2 + 2a sin '

c	v. 25 березня 2014 р.
Є. Д. Бiлоколос, Л. Д. Зайцева, Д. Д. Шека, 2014

14	Глава 1. Основнi поняття комплексного аналiзу

Множинi точок сфери вiдповiдає велике коло тодi i тiльки тодi, коли ця множина належить деякiй площинi, яка проходить через центр сфери. У випадку сфери Рiмана така площина задовольняє рiвняння A + B + C( 1=2) = 0; де A; B; C — це деякi константи, якi одночасно не дорiвнюють 0 (тобто для кожного набору параметрiв A; B; C площина, яка задовольняє вказане рiвняння, проходить через точку (0; 0; 1=2) — центр сфери Рiмана). Таким чином, потрiбно знайти, при якому значеннi параметра a знайдуться

константи A; B; C такi, що рiвнiсть A + B + C( 12) = 0 виконується для

всiх точок z; якi лежать на колi jz ij = a: Пiдставимо в цю рiвнiсть знайденi вирази для ; ; :

Aa cos ' + B(a sin ' + 1) + C(1 + a2 + 2a sin ') 0 2 + a2 + 2a sin '

для всiх ' 2 ( ; ]: Знаменник завжди бiльше 0 при довiльних a > 0; ' 2 ( ; ]: Чисельник тотожно дорiвнює 0 тодi i тiльки тодi, коли коефiцiєнти при sin '; cos ' i вiльний член дорiвнюють 0 одночасно. Запишемо цю умову

(Aa = 0;

aB + aC = 0;

2B + a2C = 0:

Оскiльки a > 0; то A = 0; C = B i, з третього рiвняння, B(2 a2) = 0: p

B 6= 0 (тодi A = B = C = 0) i a =p 2:

Таким чином, колу jz ij = 2 комплексної площини вiдповiдає велике коло на сферi Рiмана. I

Приклад 2.5. C Знайти матричне зображення числа z:1 B

Розв’язання. J Нехай z = x + iy: Даному числу вiдповiдає така матриця

z =	y	x	:
	x	y

Оскiльки при такому ототожненнi всi алгебраїчнi операцiї виконуються за звичайними правилами матричної алгебри, то

y x

1

y x

x

y

z

x2 + y2

x2

+y2

x2+y2

1

x y

1

x y

2

+y2

x2+y2

=

=

= x

y

x

:

I

Завдання для класної роботи i домашнi завдання.

В прикладах 33–44 визначити геометричний смисл вказаних спiввiдношень.

33.jz z0j = R z0 2 C; R > 0:

34.jz z0j < R z0 2 C; R > 0:

35.jz z0j R; z0 2 C; R > 0:

36.Re z C; C 2 R:

v. 25 березня 2014 р.	c
	Є. Д. Бiлоколос, Л. Д. Зайцева, Д. Д. Шека, 2014

Роздiл 2.

Способи зображення комплексних чисел

15

37.

Im z < C; C 2 R:

42.

z1; z2 2 C; a > 0:

38.

< arg z < ; ; 2 R; < :

jz z1j + jz

1z2j = 2a;

39.

< arg(z z0) < ;

z1; z2 2 C; a >

2jz2 z1j:

; 2 R; < ; z0 2 C:

43.

Re

z z1

= 0;

z1

; z2

2

C:

40.

2 C

z z2

z

z

=

z

z

; z ; z

:

j

1j

j

2j

1

2

44.

Im

z z1

= 0;

z

; z

2

C

:

41.

z z2

jz z1j jz z2j = 2a;

1

2

В прикладах 45–55 зобразити на C-площинi множину точок, яка задо-

вольняє вказану рiвнiсть або нерiвнiсть.

45.

Re

z 3 + i

> 0:

Im

z 1 2i

< 1:

50.

z i

z + 3 i

46.

Re

z 2

< 0:

51.

Re z + Im z < 1:

z + 1 + 2i

52.

jzj < Re z + 1:

47.

Re

z 4 i

> 4:

53.

i)) < p

:

Im(z(1

2

z + 2

i

z

z

48.

Im z

i

2 > 0:

54.

z

z2

= ;

> 0:

z + i

1

z

3i

1

i

z

49.

Im

< 0:

55.

0 < arg

<

:

z + i

z + 1

2

В прикладах 56–59 визначити сiм’ю лiнiй, яка задана рiвнянням.

56.

1

= C; C 2 R:

58.

1

= C; C 2 R:

Re

Im

z

z

57.

Re z2 = C; C 2 R:

59.

Im z2 = C; C 2 R:

В прикладах 60–61 за допомогою геометричних мiркувань довести спiввiдношення.

60.jz1 + z2j jz1j + jz2j z 2 C:

61.

jz1 + z2j 21 (jz1j

+ jz2j)

z1

+

z2

; z1; z2 2 C:

jz1j

jz2j

В прикладах 62–67 знайти

образ точки

на сферi Рiмана.

62.

1:

64. 1 i:

66. 2 + 2i:

63.

65.

3 + i

:

67.

1 i

:

2

8

i:

p

p

на.

В прикладах 68–71 знайти образ вказаної множини точок на сферi Рiма-

68.

arg z = ; R > 0:

71.

jzj > 1:

69.

jzj = R; R > 0:

72.

Imz > 0:

70.

jzj < 1:

73.

Imz < 0:

В прикладах 72–79 знайти матричне зображення комплексного числа.

c	v. 25 березня 2014 р.
Є. Д. Бiлоколос, Л. Д. Зайцева, Д. Д. Шека, 2014

16

Глава 1.

Основнi поняття комплексного аналiзу

74.

77.

(z 2i)2 + 1:

z:

2

78.

i(2z +

)2:

75.

jzj

:

z

79.

i

76.

z2 + i:

:

z + 1

80. Довести, що для довiльних A > 0; C 2 R; B 2 C таких, що AC < jBj2 рiвняння

A jzj2 + Bz + Bz + C = 0

є рiвнянням кола. Знайти радiус i центр цього кола.

z a

81. Для довiльного a 2 C такого, що Im a > 0 довести, що величина z a

бiльша за 1 у верхнiй пiвплощинi, менша за 1 у нижнiй пiвплощинi, дорiвнює 1 на дiйснiй осi.

82. Нехай точки z1; z2; z3 лежать на колi з центром в початку координат. Довести, що трикутник з вершинами в цих точках є рiвностороннiм тодi i лише тодi, коли z1 + z2 + z3 = 0.

83. Нехай точки z1; z2; z3 — три вершини паралелограма (точки занумерованi в порядку обходу кола). Довести, що точка є внутрiшньою точкою цього паралелограма тодi i лише тодi, коли iснують числа a; b; c 2 (0; 1) такi, що a + b + c = 1 i = az1 + bz2 + cz3: Показати, що для кожної внутрiшньої точкичисла a; b; c визначаються єдиним чином.

84.Довести спiввiдношення 2.1, якi дають взаємозв’язок мiж коoрдинатами точки на комплекснiй площинi i на сферi Рiмана.

85.Для заданого 2 R визначити, при якому значеннi параметра R колу jz j = R вiдповiдає велике коло на на сферi Рiмана.

86.Довести, що колу на сферi Рiмана вiдповiдає коло або пряма на комплекснiй площинi, причому пряма вiдповiдає в тому i лише в тому випадку, коли коло на сферi Рiмана проходить через точку N (пiвнiчний полюс).

§ 3. Добування кореня з комплексного числа

Число z1 називається коренем n-го степеня (n 2 N) з комплексного числа

z, якщо z = z1n: Нехай z = ei'; z1 = 1ei'1 ; тодi z1 = z1=n; якщо = n1 ,

' = n'1:

Алгебраїчне рiвняння zn = a, де a = jajei , n 2 N при a 6= 0 має рiвно n рiзних коренiв, якi обчислюються за формулою

p

zk = n jajei( +2 k)=n; k = 0; n 1:

На комплекснiй площинi коренi рiвняння zn = a зображуються точками, розташованими у вершинах правильного n-кутника, вписаного у коло радiуса

p

n jaj з центром у початку координат (див. рис. 6).

v. 25 березня 2014 р.	c
	Є. Д. Бiлоколос, Л. Д. Зайцева, Д. Д. Шека, 2014

	Роздiл 3. Добування кореня з комплексного числа						17
	Надалi ми позначатимемо через z1=n множину					iy	C
	всiх значень кореня n-го степеня з комплексного			z1
	числа z; через pn		— арифметичнi (дiйснi невiд’єм-
	нi) значення кореня з дiйсного числа .					2 =n	z0
	Приклад 3.1. C Розв’язати рiвняння z2 + 1 =					=n
	0; z3 + 1 = 0: B
					0		x
	Розв’язання. J Перш нiж переходити до розв’яза-
	ння рiвнянь, зауважимо, що на множинi дiйсних
	чисел перше рiвняння не має жодного кореня, а
	друге рiвняння має рiвно один корiнь z = 1:
	На множинi комплексних чисел перше рiвнян-			Рис. 6: Добування корення
	ня має два рiзних кореня:
				з комплексного числа

z = ( 1)1=2 = ei( +2 k)=2; k = 0; 1: z0 = ei =2 = i; z1 = ei3 =2 = i:

На множинi комплексних чисел перше рiвняння має три рiзних кореня:

z = ( 1)1=3 = ei( +2 k)=3; k = 0; 1; 2:

ip

ip

1

3

1

3

z0 = ei =3 =

+

; z1 = ei = 1; z2 = ei5 =3 =

:

2

2

2

2

I

Приклад 3.2. C Обчислити всi значення ( p

+ i)1=6

: B

3

p

в показниковiй формi

Розв’язання. J Позначимо z = 3 + i: Запишемо z

z = 2ei( =6+2 k): Тодi

p

z1=6 = 6 2ei( =6+2 k)=6; k = 0; 5:

p

Таким чином, вираз ( 3 + i)1=6 має шiсть рiзних значень:

p p p

z0 = 6 2e i =36; z1 = 6 2e i11 =36; z2 = 6 2e i23 =36;

p p p

z3 = 6 2e i35 =36; z4 = 6 2e i47 =36; z5 = 6 2e i59 =36:

I

Приклад 3.3. C Обчислити всi значення (3 2i)1=5: B

Розв’язання. J Позначимо z

= 3 2i: Запишемо z в показниковiй формi

z = p

13

ei( arctg 2=3+2 k): Тодi

z1=5 =

p

ei( arctg 2=3+2 k)=5; k = 0; 4:

13

10

Таким чином, вираз (3 2i)1=5

має п’ять рiзних значень:

z0 = p

ei( arctg 2=3)=5; z1

= p

ei( arctg 2=3+2 )=5; z2 = p

e i( arctg 2=3+4 )=5

;

13

13

13

10

10

10

z3 = p

e i( arctg 2=3+6 )=5; z4 = p

e i( arctg 2=3+8 )=5

:

13

13

10

10

I

Завдання для класної роботи i домашнi завдання.

В прикладах 87–96 обчислити всi значення кореня i побудувати їх.

c	v. 25 березня 2014 р.
Є. Д. Бiлоколос, Л. Д. Зайцева, Д. Д. Шека, 2014

18				Глава 1.	Основнi поняття комплексного аналiзу
87.	i1=4.		89.	( 3 + 5i)2=3.			91.	(8 + i)1=8.
88.	(2 2i)1=6.		90.	( 7 9i)1=5.			92.	(3 4i)1=7.

93. Довести, що для будь-якого комплексного числа z = x + iy справедливо:

!

			r			r		p
			2			2
(x + iy)1=2	=			+ x	+ i signy		x	; де = x2 + y2: (3.1)

В прикладах 94–99, використовуючи результат задачi 93, знайти всi значення кореня:

94.	( 9 + 2i)1=2.				96.	(7 + 4i)1=2.							98.	( 2 + 12i)1=2.
95.	(11 3i)1=2.				97.	( 8 5i)1=2.							99.	(6 9i)1=2.
	В прикладах 100–105, знайти всi розв’язки рiвнянь:
100.		z4		1 = 0.			z6		2 = ip		.		104.		(z + 1)4 = 4i 7.
					102.					3
101.		z	5	+ 1 = i.					7						5
					103.		(z + i) + i = 0.						105.		z = 6i 8.

106.Скiльки значень має вираз zn=m, де z 2 C; n; m 2 N; m 6= 0?

107.За якої умови множини значень z1=m n i (zn)1=m збiгаються?

108.Довести, що всi вершини довiльного правильного n-кутника, який ле-

	жить в	комплекснiй площинi, задаються формулою		k
				zk = aw + b; k = 0; n 1;
		2 i=n	; a; b 2 C:
	де w = e

§ 4. Елементарнi трансцендентнi функцiї

Показникова функцiя ez, z 2 C визначається наступним спiввiдношенням

exp z = ez = ex+iy = ex (cos y + i sin y) :

(4.1)

Тригонометричнi функцiї sin z, cos z, z 2 C визначаються за формулами Ейлера:

sin z =	eiz e iz	;	cos z =	eiz + e iz	;	(4.2)
	2i
			2
звiдки
	eiz = cos z + i sin z:					(4.3)

Тригонометричнi функцiї tg z; ctg z визначаються за допомогою рiвностей:

	tg z =	sin z	;	ctg z =	cos z	:	(4.4)
		cos z			sin z

Функцiя tg z визначена на множинi Cnfz : cos z = 0g = Cnf =2 + n; n 2 Zg; функцiя ctg z — на множинi Cnfz : sin z = 0g = Cnf n; n 2 Zg: Для тригонометричних функцiй залишаються справедливими всi формули тригонометрiї.

v. 25 березня 2014 р.	c
	Є. Д. Бiлоколос, Л. Д. Зайцева, Д. Д. Шека, 2014

Роздiл 4. Елементарнi трансцендентнi функцiї

19

Гiперболiчнi функцiї комплексного аргументу визначаються за допомогою рiвностей:

ch z =

ez + e z

;

sh z =

ez e z

;

thz =

sh z

;

cth z =

ch z

:

(4.5)

ch z

sh z

2

2

Функцiя thz визначена на множинi Cnfz : ch z = 0g = Cnfi =2 + ni; n 2 Zg; функцiя cth z — на множинi Cnfz : sh z = 0g = Cnf ni; n 2 Zg:

Функцiї sin z, cos z є перiодичними з дiйсним перiодом 2 , функцiї tg z, ctg z є перiодичними з дiйсним перiодом . Аналогiчно, функцiї ez, sh z, ch z є перiодичними з уявним перiодом 2 i, функцiї thz, cth z є перiодичними з уявним перiодом i . Зауважимо, що на множинi комплексних чисел функцiї sin z, cos z, z 2 C не є обмеженими.

Логарифм визначається як функцiя, обернена до експоненти. Число w 2 C називається логарифмом числа z i позначається w = Ln z, якщо ew = z.

Якщо z = jzjei(arg z+2 n) = eln jzj+i(arg z+2 n); n 2 Z; тодi

Ln z = ln jzj + i Arg z = ln jzj + i(arg z + 2 n) = ln + i(' + 2 n); n 2 Z: (4.6)

Функцiя Ln z визначена на множинi Cnf0g: Зауважимо, що на множинi комплексних чисел функцiя Ln z; z 2 C є багатозначною, її уявна частина визначена з точнiстю до числа, кратного 2 . Через ln z; z 2 C позначається будьяке iз значень функцiї Ln z:

Узагальнена степенева функцiя визначається спiввiдношенням
za = ea Ln z; z 2 C; a 2 C:	(4.7)

Нехай a = + i 2 C; z = ei('+2 n); n 2 Z; тодi:

w = za = ea Ln z = e( +i )(ln +i('+2 n)) = e ln ('+2 n)+i( ln + ('+2 n)) =

h i

= e ln ('+2 n) cos [ ln + (' + 2 n)) + i sin( ln + (' + 2 n)) :

Узагальнена степенева функцiя є багатозначною на множинi комплексних чисел, якщо a 62Z:

Аналогiчно визначається узагальнена показникова функцiя:
az = ez Ln a; z 2 C; a 2 C:	(4.8)

Нехай a = jajei( +2 n), n 2 Z, 6= 0, z = x + iy; тодi:

w= az = ez Ln a = e(x+iy)(ln jaj+i( +2 n)) = ex ln jaj y( +2 n)+i(y ln jaj+x( +2 n)) =

= ex ln jaj y( +2 n) (cos(y ln jaj + x( + 2 n)) + i sin(y ln jaj + x( + 2 n))) :

Оберненi тригонометричнi i гiперболiчнi функцiї Arcsin z, Arccos z, Arctg z, Arcctg z, Arsh z, Arch z, Arth z, Arcth z визначаються як функцiї оберненi до функцiй sin w, cos w, tg w, ctg w, sh w, ch w, thw, cth w, вiдповiдно. Наприклад, число w 2 C називається арксiнусом числа z i позначається

c	v. 25 березня 2014 р.
Є. Д. Бiлоколос, Л. Д. Зайцева, Д. Д. Шека, 2014

20 Глава 1. Основнi поняття комплексного аналiзу

w = Arcsin z; якщо z = sin w: Всi оберненi тригонометричнi функцiї є багато-

значними i виражаються через логарифмiчну функцiю:

Arcsin

= iLn 1 + iz

i

z + i

z

i

iz + (1

z2)1=2 ;

Arccos z =

i Ln z + (z2

1)1=2 ;

Arctg z

=

Ln

;

Arcctg z =

Ln

;

2

1 iz

2

z i

Arsh

=

1

1 + z

1

z + 1

z

Ln

z + (z2 + 1)1=2 ;

Arch z = Ln

z + (z2

1)1=2 ;

Arth z

=

Ln

;

Arcth z =

Ln

:

2

1 z

2

z 1

Через arcsin z, arccos z, arctg z, arcctg z, arsh z, arch z, arth z, arcth z, z 2 C

позначається будь-яке iз значень функцiй Arcsin z, Arccos z, Arctg z, Arcctg z,

Arsh z, Arch z, Arth z, Arcth z, вiдповiдно.

Приклад 4.1. C Обчислити суму sin z + sin 2z + : : : + sin nz; n 1; z 2 C: B

Розв’язання. J Скористаємось означенням функцiї sin z для кожного доданка:

z

sin 2z + : : : + sin nz =

1

eiz

e iz + e2iz

e 2iz + : : : + einz

e inz

=

sin

1

+ iz

2iz

inz

2i

iz

2iz

inz

=

e + e

+ : : : + e

e

+ e

+ : : : + e

=

2i

1

eiz

ei(n+1)z

e iz e i(n+1)z

2i

1 eiz

1 e iz

=

=

=

eiz ei(n+1)z 1 + einz e iz + e i(n+1)z + 1 e inz

=

2i (1 eiz e iz + 1)

=

2i sin z + 2i sin nz 2i sin(n + 1)z

=

sin z + sin nz sin(n + 1)z

:

2i (2 2 cos z)

2(1 cos z)

В третiй рiвностi ми скористалися вiдомою формулою для обчислення суми геометричної прогресiї, в п’ятiй — означеннями тригонометричних функцiй.

I

Приклад 4.2. C Знайти всi точки z, в яких функцiя thz приймає дiйснi значення. B

Розв’язання. J Iншими словами, потрiбно знайти всi z 2 C такi, що Im thz = 0: Нехай z = x + iy; тодi

thz = th(x + iy) =

ex+iy e x iy

=

ex(cos y + i sin y) e x(cos y i sin y)

=

ex(cos y + i sin y) + e x(cos y i sin y)

ex+iy + e x iy

=

cos y(ex e x) + i sin y(ex + e x)

=

cos y sh x + i sin y ch x

=

cos y(ex + e x) + i sin y(ex e x)

cos y ch x + i sin y sh x

cos

2 y

sh

x

ch

x

sin

2 y sh x ch x + i

ch2 x sin y cos y

sh2 x sin y cos y

=

cos2 y ch2 x

+ sin2 y sh2 x

=

y

y

=

sh x ch x cos 2y + i sinpcos

;

p

cos2 y ch2 x + sin2 y sh2 x

v. 25 березня 2014 р.	c
	Є. Д. Бiлоколос, Л. Д. Зайцева, Д. Д. Шека, 2014