complan_taskbook_1

Роздiл 8. Iнтеграл вiд функцiї комплексної змiнної

51

316. Обчислити iнтеграл
	Ik = Z tg2 zdz; k = 1; 2; 3;
	k
якщо
а) 1	— це ромб з вершинами в точках i; =4; i; =4;
б) 2	— це вiдрiзок, який з’єднує точки z1 = =4 i z2 = i;
в) 3	— це ламана z1z3z2, де z3 = 0:

В прикладах 317–308 обчислити iнтеграл I вздовж кривої :

317.

z sh z2dz, якщо =

z : jzj = p

:

I =

2

318.

R

e

z2

I =

dz, якщо — це трикутник з вершинами в точках 1 + 2i; i;

1 + 2i:

R

th2zdz, якщо = fz

: jzj = 1g :

319.

I =

320.

R

dz

I =

, якщо — це прямокутник з вершинами в точках 2 + 2i;

z2

5

2

2i;

2i; 2 + 2i:

2 R

321.

I =

(2z + i)11 dz, якщо — це вiдрiзок, який з’єднує точки 1 + i=2 i

i:

R

sin iz cos 4izdz, якщо = fz : jzj = =2; 0 < arg z < =2g :

322.

I =

R e3iz + 1

323.

I =

dz, якщо — це вiдрiзок, який з’єднує точки i ln 2 i 2 :

eiz + 1

324.

I = R

ch3 zdz, якщо = fz

: jzj = ; =2 < arg z < g :

325.

R

(z + 1) sh zdz, якщо — це вiдрiзок, який з’єднує точки i i 1:

I =

326.

I = R (iz + 1) eizdz, якщо = fz : jzj = ; 0 < arg z < =2g :

327.

I = R z2 sin zdz, якщо — це вiдрiзок, який з’єднує точки 2i i =2:

z2 + 2z + 1 ch zdz, якщо — це ламана, який з’єднує точки 1;

328.

I = R

R

0i i:

Вприкладах 329–346 обчислити iнтеграл I вiд заданої вiтки багатозначної функцiї вздовж кривої :

R	dz			p3
329. I = p3			; якщо = fz : jzj = 1g ; за умови		1 = 1.
		z

c	v. 25 березня 2014 р.
Є. Д. Бiлоколос, Л. Д. Зайцева, Д. Д. Шека, 2014

52	Глава 2. Аналiтичнi функцiї. Iнтегрування функцiй комплексної змiнної

331.	I = R	z	p
			3idz; якщо = fz
330.	I =	z		2dz; якщо = fz
	R	4
332.	I = R	p				dz; якщо = fz
				z

p

: jzj = 1g ; за умови 1 2 = 1.

: jzj = 1g ; за умови 13i = 1.

p

: jzj = 1g ; за умови 4 1 = i.

p

p

p

333.

R

dz

jzj = 1g ; за умови 1 3 = e4 i

3.

I =

z

3dz; якщо = fz

:

z2i+1 ; якщо = fz

: jzj = 1g ; за умови 12i+1 = e2 (i 2).

334.

I =

R

335.

R

Ln zdz; якщо = fz

: jzj = 1g ; за умови Ln 1 = 6 i.

I =

336.

R

Ln zdz; якщо = fz

: jzj = 5g ; за умови Ln 5 = ln 5 + 8 i.

I =

337.

R

jLn zj dz; якщо = fz

: jzj = 1g ; за умови Ln 1 = 2 i.

I =

Ln z

338.

R

: jzj = 1g ; за умови Ln( 1) = 3 i.

I =

jLn zj dz; якщо = fz

R

Ln z

339.

I =

z

dz; якщо = fz

:

jzj = eg ; за умови Ln e = 1.

341.

I = R

z

5

Ln zdz; якщо = fz

: jzj = 1g ; за умови Ln 1 = 0.

340.

I =

z

dz; якщо = fz

:

jzj = 4g ; за умови Ln 4 = ln 4 2 i.

342.

I = R

z9 Ln zdz; якщо = fz

: jzj = 1g ; за умови Ln( 1) = i.

R

3

Ln zdz; якщо = fz

: jzj = 2g ; за умови Ln 2 = ln 2 + 4 i.

343.

I = R z

: jzj = 1g ; за умови Ln 1 = 0.

344.

I = R jLn zj2 dz; якщо = fz

: jzj = 1g ; за умови Ln 1 = 4 i.

345.

I = R jLn zj2 dz; якщо = fz

346. I = R jLn zj2 dz; якщо = fz : jzj = 1=2g ; за умови Ln 1=2 = ln 2 +

2 i.
347. Для заданого 2 R обчислити
I = Z	z dz;

якщо = fz : jzj = 1g ; за умови 1 = e2 ik0 ; k0 2 Z. 348. Для заданого 2 R обчислити

Z

I = zi dz;

v. 25 березня 2014 р.	c
	Є. Д. Бiлоколос, Л. Д. Зайцева, Д. Д. Шека, 2014

jdzj 2 R

jz ajjz + aj < jR2 jaj2j:

Роздiл 8. Iнтеграл вiд функцiї комплексної змiнної

53

якщо = fz : jzj = 1g ; за умови 1i = e 2 k0 ; k0 2 Z. 349. Для заданого 2 C обчислити

Z

I = z dz;

якщо = fz : jzj = 1g ; за умови 1 = e2 ik0 ; k0 2 Z. 350. Обчислити

Z

I = Ln zdz;

якщо = fz : jzj = Rg ; за умови Ln R = ln R + 2 ik0; k0 2 Z. 351. Обчислити

Z

I = jLn zj dz;

якщо = fz : jzj = 1g ; за умови Ln 1 = 2 ik0; k0 0. 352. Обчислити

I = Z	z dz;
	Ln z

якщо = fz : jzj = Rg ; за умови Ln R = ln R + 2 ik0; k0 2 Z. 353. Для заданого n 2 Znf 1g обчислити

Z

I = zn Ln zdz;

якщо = fz : jzj = Rg ; за умови Ln R = ln R + 2 ik0; k0 2 Z. 354. Обчислити

Z

I = jLn zj2 dz;

якщо = fz : jzj = Rg ; за умови Ln R = ln R + 2 ik0; k0 2 Z. 355. Довести, якщо jaj 6= R, то

Z

jzj=R

356. Довести, якщо jaj 6= R, то		= jR2 jaj2j:
Z	jzj ajj2
	dz		2 R

jzj=R

357. Нехай f(z) 2 C (fz :

lim

"!0

jz z0j Rg)) для деякого R > 0. Довести, що

Z

f(z)

z z0 dz = 2 i f(z0):

jz z0j="

c	v. 25 березня 2014 р.
Є. Д. Бiлоколос, Л. Д. Зайцева, Д. Д. Шека, 2014

54	Глава 2. Аналiтичнi функцiї. Iнтегрування функцiй комплексної змiнної

§ 9. Iнтегральна формула Кошi

Якщо функцiя f(z) є аналiтичною в областi D i неперервною в D, тодi для довiльного z0 2= @D має мiсце iнтегральна формула Кошi:

2 i Z		z z0		0;	z0	2= D;
1		f(z)	dz =	f(z0);	z0	2	D		(9.1)
	@D

напрямок обходу контуру @D додатний (так, що область D залишається лiворуч). Вираз в лiвiй частинi формули (9.1) має назву iнтеграл Кошi. Важливою властивiстю цього iнтеграла є iснування i аналiтичнiсть всiх похiдних довiльного порядку, так звана iнтегральна формула Кошi для похiдних:

2 !i Z		(z	f	(z0)n+1 dz =
n				z)
	@D

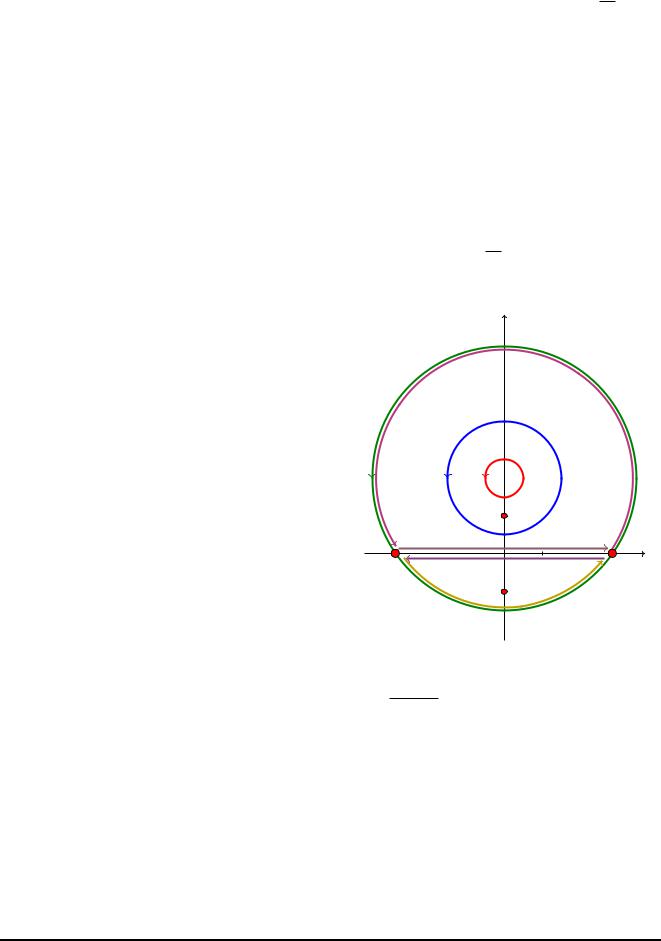
Приклад 9.1. C Обчислити iнтеграл

Ik = Z	z2 + 1 ; k = 1; 2; 3;
	sin zdz
k
якщо

а) 1 = fz : jz 2ij = 1=2g ;

б) 2 = fz : jz 2ij = 3=2g ;

в) 3 = fz : jz 2ij = 7=2g :

B

f(n)(z0);	z0 2 D			(9.2)
0;	z0 2= D;
			iy
				3
			2
			1
				+
		i	z	3
			1	+
2		0	1	1 x
			z2 3

Рис. 15: До прикладу 9.1

sin z

Розв’язання. J а) Пiдiнтегральна функцiя z2 + 1 є аналiтичною в областi

jz 2ij 3=4; яка мiстить замкнений контур 1; тому за iнтегральною формулою Кошi (9.1) для випадку, коли особлива точка не належить областi,

випливає, що	z2 + 1 = 0:
I1 = Z
	sin zdz
1

Цей результат можна отримати також, пригадавши iнтегральну теорему Кошi (8.7).

б) Всерединi областi, яка обмежена контуром 2; знаходиться одна точка z1 = i; в якiй знаменник пiдiнтегральної функцiї обертається в нуль.

v. 25 березня 2014 р.	c
	Є. Д. Бiлоколос, Л. Д. Зайцева, Д. Д. Шека, 2014

= 2 i

Роздiл 9. Iнтегральна формула Кошi

55

Перепишемо iнтеграл у виглядi

(z + i)(z i) = Z2

I2 = Z2 z2 + 1 = Z2

sin z

dz

zz+ i i :

sin zdz

sin zdz

Функцiя

sin z

є аналiтичною в областi, яка обмежена 2: Застосувавши

z + i

iнтегральну формулу Кошi (9.1), отримаємо

Z2

sin z

dz

2i = i sh 1:

zz+ i i = 2 i z + i z=i

sin z

sin i

в) Всерединi областi, яка обмежена контуром 3; знаходяться двi точки z1 = i i z2 = i; в яких знаменник пiдiнтегральної функцiї обертається в нуль. Тому беспосередньо застосовувати iнтегральну формулу Кошi для обчислення I3 не можна. Розглянемо два способи обчислення iнтегралу.

I СПОСIБ. Скористаємося лiнiйною властивiстю iнтегралiв: зведемо пiдiнтегральну функцiю до виразу, в якому зможемо безпосередньо скористатися

1

iнтегральною формулою Кошi, розклавши z2 + 1 на елементарнi дроби:

1			1	1			1		1
		=									:
z2 + 1			2i		z i		2i			z + i

Тодi можемо переписати шуканий iнтеграл у виглядi:

I3 = Z	z2 + 1	= 2i Z			z i	2i Z			z + i
	sin zdz	1			sin zdz	1			sin zdz
3				3				3

Застосувавши iнтегральну формулу Кошi (9.1) для кожного з iнтегралiв,

	отримаємо	2 i		2 i
	I3 =		sin i		sin( i) = 2 i sh i:
		2i		2i

II СПОСIБ. Скористаємося властивiстю адитивностi iнтегралу: подамо контур iнтегрування у виглядi об’єднання таких контурiв, для кожного з яких

можна скористатися iнтегральною формулою Кошi. Для цього позначимо
	p			p
1 =		33	; 2 =		33			(це точки, в яких 3 перетинає вiсь абсцис) та
	2			2

розглянемо наступнi додатковi контури (див. рис. 15):

+ = fz : z(t) = 2 + ( 1 2)t; t 2 [0; 1]g (верхнiй берег розрiзу [ 2; 1]);

= fz : z(t) = 1 + ( 2 1)t; t 2 [0; 1]g (нижнiй берег розрiзу [ 1; 2]);

3+ = fz	: jz 2ij = 3=2; Im z 0g	(пiвколо вiд 1	до 2);
3 = fz	: jz 2ij = 3=2; Im z < 0g	(пiвколо вiд 2	до 1).

c	v. 25 березня 2014 р.
Є. Д. Бiлоколос, Л. Д. Зайцева, Д. Д. Шека, 2014

56 Глава 2. Аналiтичнi функцiї. Iнтегрування функцiй комплексної змiнної

Зауважимо, що 3

= +

;

крiм того,

sin zdz

= 0. Перепишемо

3

3

+RS z2 + 1

iнтеграл I3 наступним чином:S

+Z

3 =Z3

z2 + 1

+Z

z2

+ 1

z2 + 1

+

Z +

z2 + 1

I

sin zdz

=

sin zdz

+

sin zdz

=

sin zdz

=

3

3

S

3

3

sin z

S

sin z

S

S

S

3

sin zdz

3

sin zdz

Z3

Z3

idz

+

=+Z

+ Z

=

z + i

+

zz + i

:

+z2 + 1

z2 + 1

z i

S

S

+

S

S

Кожний з контурiв 3+

+ i 3

є кусково-гладким i замкненим, при-

чому напрям обходу

кожного контуру є додатним. Всерединi кожного з цих

S

S

контурiв знаходиться по однiй точцi, в якiй знаменник обертається в нуль. Функцiї, якi стоять в чисельниках, є аналiтичними у вiдповiдних областях. Тому для кожного з iнтегралiв можна застосувати iнтегральну формулу Кошi (9.1):

Z4 2	sin z	dz			z=i
			= 2 iz + i			= 2 i 2i = i sh 1;
	zz+ i i
				sin z		sin i
S

Z5 1	sin z dz
	zz + i
	i
S

Таким чином,

	z	i					2i
= 2 i	sin z		z= i		= 2 i	sin( i)			= i sh 1:

I3 = 2 i sh 1:

I

Приклад 9.2. C Обчислити iнтеграл

I = Z	(zcos2 i)3 ;
	z	izdz

якщо = fjzj = 7g : B

v. 25 березня 2014 р.	c
	Є. Д. Бiлоколос, Л. Д. Зайцева, Д. Д. Шека, 2014

Роздiл 9. Iнтегральна формула Кошi

57

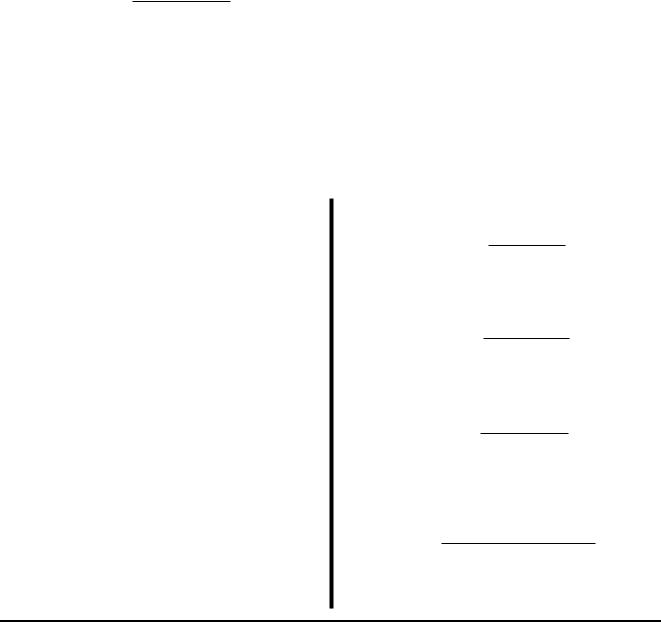
Розв’язання. J Всерединi областi, яка обмежена контуром ; знаходиться одна точка z0 = 2 i; в якiй знаменник пiдiнтегральної функцiї обертається в нуль (див. рис. 16). Функцiя z cos iz є аналiтичною в областi, яка обмежена : Застосувавши iнтегральну формулу Кошi для похiдних (9.2) для n = 3, отримаємо

I = Z

(zcos2 i)4

=

23!

(z cos iz)000

z=2 i

=

z

izdz

i

i

h

= 3

i z=2 i

3(cos iz)00

+ z(cos iz)000

=

i

2

3

3i

cos iz

zi

sin iz

z=2 i

3

=

= i:

I

iy

z0

	i
0	1	x

Рис. 16: До прикладу 9.2

358. Обчислити iнтеграл
Ik = Z				zezdz
					;		k = 1; 2; 3;
				z2 + 4
	k
якщо
а) 1 = fz : jz + ij = 1=4g ;							в) 3 = fz : jz + ij = 7=2g :
б) 2 = fz : jz + ij = 2g ;
359. Обчислити iнтеграл
Ik = Z		ch2 zdz					k = 1; 2; 3; 4;
						;
	z (z2 + 2)
k
якщо
а) 1 = fz : jz 4ij = 1=3g ;							в) 3 = fz : jz 4ij = 13=3g ;
б) 2 = fz : jz 4ij = 4=3g ;							г) 4 = fz : jz 4ij = 25=3g :
360. Обчислити iнтеграл			4z2 2 ;
Ik = Z							k = 1; 2; 3;
			z sin zdz

k

якщо

c	v. 25 березня 2014 р.
Є. Д. Бiлоколос, Л. Д. Зайцева, Д. Д. Шека, 2014

58

Глава 2. Аналiтичнi функцiї. Iнтегрування функцiй комплексної змiнної

а) 1 = fz : jz 1j = 1=5g ;

в) 3 = fz : jz 1j = 3g :

б) 2 = fz : jz 1j = 1g ;

361. Обчислити iнтеграл

Ik = Z

2eiz

z

z d

;

k = 1; 2; 3; 4;

(z 1) (z2 + 9)

k

якщо

а) 1 = fz : jz 4ij = 1=2g ;

в) 3 = fz : jz 4ij = 9=2g ;

б) 2 = fz : jz 4ij = 3=2g ;

г) 4 = fz : jz 4ij = 15=2g :

В прикладах 362–365, обчислити iнтеграл:

362.

364.

Z

Z

z5(i z2)dz

:

z2 ch( z)dz

:

(z + i)5

(z

i)7

z+i =4

jz 1j=3

365.

j j

363.

Z

eizdz

Z

3z

:

(2z + 3)e dz

:

(z

5i)10

21

jz 3ij=3

(z + 2)

jz+1j=2

В прикладах 366–377, обчислити iнтеграл:

366.				2 z			z
Z
			sin d					:
				z3
jzj=1=2
367.	ch z5						:
Z
				2zdz
jzj=1
368.				z (z2 + 9):
Z
				tg zdz
jz 1=2j=1
369.
Z					1
	(z + 1) (z + 3)2 :
				ez+2 dz

jz+1=3j=4=3

370.

Zsin ei zdz

z (z 2)2 :

jz 3j=2

371.

Z

cos 2zdz z2 (z )2 :

jz 3j=1

372.

Zz2dz

z2 + iz + 2:

jzj=5=2

373.

Z (ch z + sh 2 z) dz (z2 + 1) (z2 + 4) :

jzj=3

v. 25 березня 2014 р.	c
	Є. Д. Бiлоколос, Л. Д. Зайцева, Д. Д. Шека, 2014

Роздiл 9. Iнтегральна формула Кошi

59

374.

Z	ezdz	:
	z3 (z + 2i)
jz 1j=5=2

375.

Zz2 + i dz

z (z i)4 :

jzj= =2

376.

Z			(iz + 1) (z2	+ 1)2 :
			sh zdz
p
jzj=	2

377.

Z

dz (z2 + 9)3 :

jzj=

378. Обчислити

I =	Z	(z a)n(z b); n 1;
		dz
	jzj=R

якщо jaj < R < jbj.

379. Скiльки рiзних значень в залежностi вiд n може приймати iнтеграл

zZ=R =1(z zk)			6
I =	dz	;	zj = zk;
	n
j j	kQ

якщо jzkj =6 R; k = 1; 2; : : : n?

380. Нехай функцiя f(z) є аналiтичною в областi D i неперервною в D; а z1; : : : ; zn — довiльнi рiзнi точки в D. Позначимо

wn(z) = (z z1) : : : (z zn) :

Показати, що iнтеграл		wn( )			z n
P (z) = 2 i Z			n			d
1		f( )	w	( )	w	(z)
	@D

є многочленом (n 1)-го степеня, який спiвпадає з f(z) в точках z1, : : :, zn (многочлен P (z) називається iнтерполяцiйним многочленом Лагранжа).

c	v. 25 березня 2014 р.
Є. Д. Бiлоколос, Л. Д. Зайцева, Д. Д. Шека, 2014

Вiдповiдi

Роздiл 1

1. Re z =

3

, Im z = 2529:

25

2. Re z = 6566, Im z = 6557:

3. Re z = 2617, Im z = 2619:

4. Re z =

19, Im z =

4

:

50

25

5. Re z = 1335, Im z = 1320:

6. Re z =

6

, Im z =

8

:

25

25

7. jzj = p

; Arg z =

3

+ 2 n; n 2 Z:

2

4

8. jzj = 1313; Arg z = 2 13 arctg

5

+ 2 n; n 2 Z:

12

9. jzj = 105=718; Arg z = 36 arctg p

10 arctg 3 10 + 2 n; n 2 Z:

6

p

3

2 Z:

10. jzj = 4

2; Arg z =

+ 2 n; n

4

Z:

100

3

11. jzj = 1025=2

; Arg z = 20 100 arctg 4

+ 2 n; n 2

12. jzj =

29

; Arg z = 25 25 arctg 25 39 arctg p13 + 2 n; n 2 Z:

1439=2

13. exp

i(2 + 2 n) ; n 2 Z:

14.

3

8

f

g

; n

2 Z

:

exp

i( + 2 n)

15.

5

exp fi(16 arctg 2 11 arctg 7 + 2 n)g ; n 2 Z:

5011=2

16.

1

f

g

; n

2 Z

:

2 exp

i2 n

g 2 Z

17.

1015=2

f

2 Z:

2 exp8

i( 2 + 2 n)

; n

18.

2

exp

i(15 arctg 3

5 + 2 n) ; n

:

19. cos4 ' sin '

6

10 cos2 ' sin3 ' + sin5 ':

28 cos2

' sin6

' + sin8

':

20.

5

8 '

' sin2 ' + 70 cos4 ' sin4 '

21.

cos3

'

28 cos

2

':

cos

3 cos

'

sin

3

'

4 '

5

'

2

'

7 '

9

':

22.

8

6

9 cos ' sinx' 84 cos

' sin

y +126 cos

sin

36 cos

sin

+sin

23. Re w =

; Im w =

:

x2+y2

x2+y2

24.

2

2 y

2

+2 x2; Im w = y(23 x2+ 1):

Re w = x3

+x +xy y

y +x y+2xy

25.

Re w = xx2+y2+2x+1

; Im w =

:

x2+y2+2x+1

26. Re w = x2 y2 + 4y + 1; Im w = 2x(y 2):

29. Вказiвка.Скористатись формулою Муавра.

30. Вказiвка.Скористатись методом математичної iндукцiї.

31. Вказiвка.Скористатись тим, що для довiльного a 2 R : a = a.

Роздiл 2

33. Коло з центром в точцi z0; радiуса R:

34. Внутрiшнiсть кола з центром в точцi z0; радiуса R:

35. Коло з центром в точцi z0; радiуса R i зовнiшнiсть цього кола. 36. Пряма x = C i пiвплощина, яка лежить справа вiд неї.

37. Пiвплощина, яка лежить нижче прямої y = C:

38. Внутрiшнiсть кута з вершиною в початку координат i сторонами, якi утворюють з додатним напрямком осi Ox кути i :

60