complan_taskbook_1

Роздiл 8. Iнтеграл вiд функцiї комплексної змiнної

41

тодi

Z	b	f (z(t)) z0(t)dt = Z	b
	f(z)dz = Z		f (x(t) + iy(t)) (x0(t) + iy0(t)) dt; (8.3)
	a	a

b

ZZ

f(z) jdzj = f (z(t)) jz0(t)j dt =

a

b

Z

=f (x(t) + iy(t))

p

(x0(t))2 + (y0(t))2dt:

(8.4)

a

В частинному випадку, коли — це вiдрiзок з початком в точцi z1 = x1 + iy1 i кiнцем в точцi z2 = x2 + iy2, тодi зручно використовувати таку

параметризацiю
	= fz(t) : z(t) = (1 t)z1 + tz2 =	(8.5)
	= (1 t)x1 + tx2 + i ((1 t)y1 + ty2) ; t 2 [0; 1]g :
Якщо — це коло з центром в точцi z0 = x0 + iy0 i радiуса R (позначення
= fz	: jz z0j = Rg), тодi зручно використовувати таку параметризацiю
=	z(t) : z(t) = z0 + Reit = x0 + R cos t + i (y0 + R sin t); t 2 [0; 2 )	: (8.6)

Наведемо деякi властивостi iнтеграла (8.1) у випадку аналiтичної пiдiнтегральної функцiї f 2 A(D).

Згiдно з iнтегральною теоремою Кошi iнтеграл вiд аналiтичної функцiї по замкненому контуру, що належить областi аналiтичностi, дорiвнює нулевi:

Z

f(z)dz = 0; якщо f(z) 2 A(D), D. (8.7)

Як наслiдок, iнтеграл вiд аналiтичної функцiї не залежить вiд шляху iнтегрування, тобто для будь-яких кривих k, що належать областi D та мають спiльнi кiнцi:

k = fz(t) : t 2 [0; 1]; z(0) = z1; z(1) = z2g D;		(8.8)
iнтеграл приймає одне й те саме значення:
Z	z2
	Z	(8.9)
f(z)dz =	f(z)dz:
k	z1

Для функцiї f(z), яка є аналiтичною в однозв’язнiй областi D, має мiсце формула Ньютона—Лейбнiца:

z2	f(z)dz = (z) z1		= (z2) (z1);	(8.10)
Z
z1		z2

c	v. 25 березня 2014 р.
Є. Д. Бiлоколос, Л. Д. Зайцева, Д. Д. Шека, 2014

42	Глава 2. Аналiтичнi функцiї. Iнтегрування функцiй комплексної змiнної

тут (z) — довiльна первiсна функцiї f(z); тобто 0(z) = f(z) в областi D.

Якщо f(z) i g(z) є аналiтичними в однозв’язнiй областi D, тодi має мiсце формула iнтегрування частинами:

z2	f(z)g0(z)dz = [f(z)g(z)] z1		z2	g(z)f0(z)dz	(8.11)
Z			Z
z1		z2	z1

для довiльних z1; z2 2 D.

Замiна змiнних в iнтегралах вiд функцiї комплексної змiнної вiдбувається аналогiчно випадку функцiї дiйсної змiнної. Нехай аналiтична функцiя z = g(w) вiдображає взаємно однозначно контур 1 в w-площинi на контурв z-площинi. Тодi

ZZ

f(z)dz = f[g(w)]g0(w)dw:

1

При обчисленнi iнтегралiв вiд багатозначних функцiї будемо видiляти вiтку цiєї функцiї. Це можна зробити, наприклад, завдавши значення багатозначної функцiї в деякiй точцi контуру iнтегрування.

Зауваження. В усiх задачах, де контур замкнений, вважаємо, що обхiд контуру вiдбувається проти годинникової стрiлки.

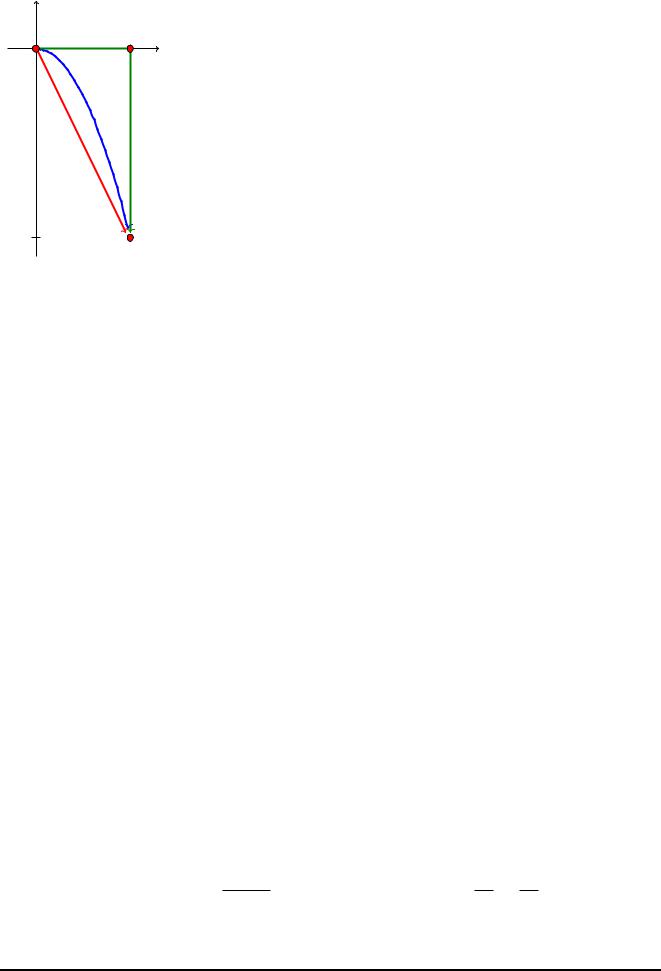
Приклад 8.1. C Обчислити iнтеграл

Z

Ik = (2z Im z + 1) dz; k = 1; 2; 3;

k

якщо

а) 1 — це вiдрiзок, який з’єднує точки z1 = 0 i z2 = 1 2i;

б) 2 — це частина параболи, яка з’єднує точки z1 i z2; за умови, що задана парабола має вершину в точцi z1 i є симетричною вiдносно уявної осi;

в) 3 — це ламана z1z3z2, де z3 = 1.

B

Розв’язання. J

v. 25 березня 2014 р.	c
	Є. Д. Бiлоколос, Л. Д. Зайцева, Д. Д. Шека, 2014

Роздiл 8. Iнтеграл вiд функцiї комплексної змiнної

43

	iy
z1	31 z3
0	1 x

2

23

1

2i

z2

Рис. 8: До прикладу 8.1

Z

Кожна з кривих 1; 2 або 3 — це лiнiя, яка з’єднує точки z1 = 0 i z2 = 1 2i по рiзних траєкторiях. Оскiльки пiдiнтегральна функцiя не є аналiтичною, iнтеграл залежить вiд шляху iнтегрування, i природно очiкувати в кожнiй ситуацiї рiзнi вiдповiдi.

а) Параметризуємо 1 аналогiчно до (8.5):

1 = fz(t) : z(t) = (1 2i) t; t 2 [0; 1]g : Тодi dz = (1 2i) dt;

2z Im z + 1 = 2 (1 + 2i) t + 2t + 1 = 4 (1 + i) t + 1;

де при знаходженнi останнього виразу ми скористалися тим, що параметр t є дiйсним.

Обчислимо iнтеграл, див. (8.3):

1

Z

I1 = (2z Im z + 1) dz = (1 2i) (4 (1 + i) t + 1) dt =

1		0
= (1 2i) 2 (1 + i) t2	+ t	1
		0 = (1 2i) (2 (1 + i) + 1) = 7 4i:
б) Параметризуємо 2 :

2 = z(t) : z(t) = x(t) + iy(t) = y(t) = 2t2			= t 2t2i; t 2 [0; 1] :
	x(t) = t;

Тодi dz = (1 4ti) dt;

2z Im z + 1 = 2 t + 2t2i t + 2t2 + 1 = (2 + 4i) t2 + 2t + 1;

при знаходженнi останнього виразу, ми скористалися тим, що параметр t — дiйсний.

Обчислимо iнтеграл, див. (8.3):

	1
I2 = Z (2z Im z + 1) dz = Z			(2 + 4i) t2 + 2t + 1 (1 4ti) dt =
2	0
1
Z

=(16 8i) t3 + (2 4i) t2 + (2 4i) t + 1 dt =

0
				2 4it3			1		20 16i:
= (4		2i) t4	+		+ (1		2i) t2 + t	=
				3			0		3 3

в) Позначимо через 13 вiдрiзок z1z3, через 23 — вiдрiзок z3z2 (див. рис. 8).

c	v. 25 березня 2014 р.
Є. Д. Бiлоколос, Л. Д. Зайцева, Д. Д. Шека, 2014

44 Глава 2. Аналiтичнi функцiї. Iнтегрування функцiй комплексної змiнної

Ламана 3 є об’єднанням цих вiдрiзкiв 3 = 31 S 32

i

I3 = Z1

(2z Im z + 1) dz + Z2

(2z Im z + 1) dz:

3

3

Параметризуємо 31

аналогiчно (8.5):

Тодi

31 = fz(t) : z(t) = t; t 2 [0; 1]g :

dz = dt;

2z Im z + 1 = 2t + 1:

Параметризуємо 32

аналогiчно (8.5):

Тодi dz = 2idt;

32 = fz(t)

: z(t) = 1 2ti;

t 2 [0; 1]g :

2z Im z + 1 = 2 (1 + 2it) + 2t + 1 = (2 + 4i) t + 3:

Обчислимо iнтеграл, див. (8.3):

1

1

I3 = Z0

(2t + 1) dt 2i Z0

((2 + 4i) t + 3) dt =

= t2

+ t

1

2i (1 + 2i) t2

+ 3t

1

0

0 = 6 8i:

I

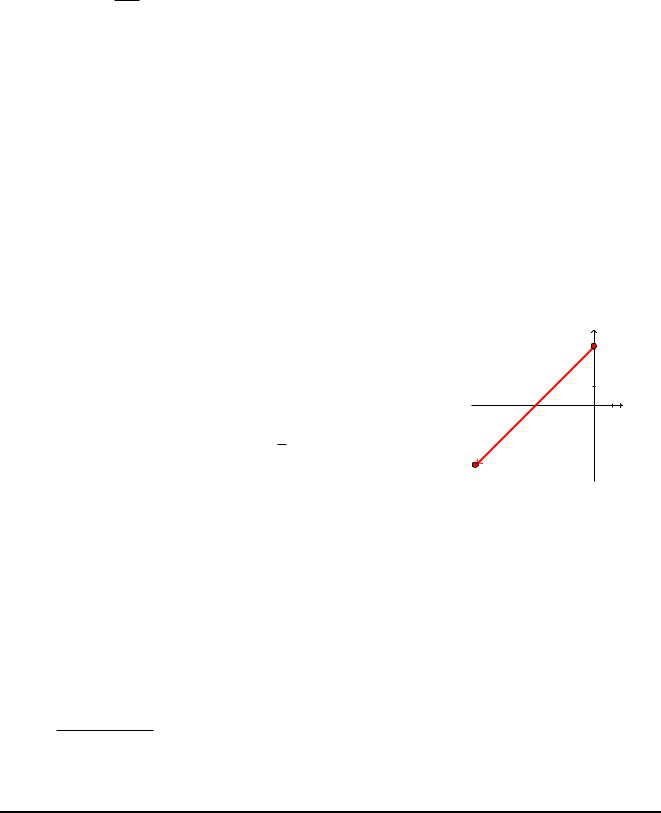
Приклад 8.2. C Обчислити iнтеграл

i

iy

I = Z

z3

zz2

dz;

0

1 x

якщо = nz : jzj

= 1;

arg z

o: B

i

2

2

Рис. 9: До

прикладу

8.2

Розв’язання. J Зауважимо, що пiдiнтегральна функцiя не є аналiтичною, iнтеграл залежить вiд шляху iнтегрування.

Параметризуємо аналогiчно (8.6):

z(t)

: z(t) = eit;

t

23hit

;

:

Тодi

= n

it

t;

z

3

zz

2

2 it2 io2it

3it

it

:

d

z

=

ie

d

=

e

e e

=

e

e

v. 25 березня 2014 р.	c
	Є. Д. Бiлоколос, Л. Д. Зайцева, Д. Д. Шека, 2014

Роздiл 8. Iнтеграл вiд функцiї комплексної змiнної

45

Обчислимо iнтеграл, див. (8.3):

I = Z

=2

=2

z3

zz2

dz = i

Z

e3it e it

eitdt = i

Z

e4it 1 dt =

=2

=2

= i

e4i

t

=2

= i :

4it

=2

I

Приклад 8.3. C Обчислити iнтеграл

Z

I = cos z jdzj ;

якщо — це вiдрiзок, який з’єднує точки z1 = i i z2 = 2 i . B

Розв’язання. J

Цей iнтеграл визначається формулою (8.2). Параметризуємо аналогiчно (8.5):

= fz(t) : z(t) = i + ( 2 2 i) t; t 2 [0; 1]g :

p

Тодi jdzj = j2 2 ij dt = 2 2dt, z = i + ( 2 + 2 i) t.

	z1	iy
	i	x
	0	1
z2
Рис. 10: До прикладу 8.3

Обчислимо iнтеграл, див. (8.4):

1

I = Z

cos z jdzj = 2 p

Z

cos ( i + ( 2 + 2 i) t) dt =

2

p

0

p

2

1

2

=

2

sin ( i + ( 2 + 2 i) t) 0

=

(sin ( i 2 ) + sin i) =

2 + 2 i

i 1

p

( i

2

1)

=

2 sin i = p2 ( i

1) i sh = p2 sh (1

i):

2

I

c	v. 25 березня 2014 р.
Є. Д. Бiлоколос, Л. Д. Зайцева, Д. Д. Шека, 2014

46	Глава 2. Аналiтичнi функцiї. Iнтегрування функцiй комплексної змiнної

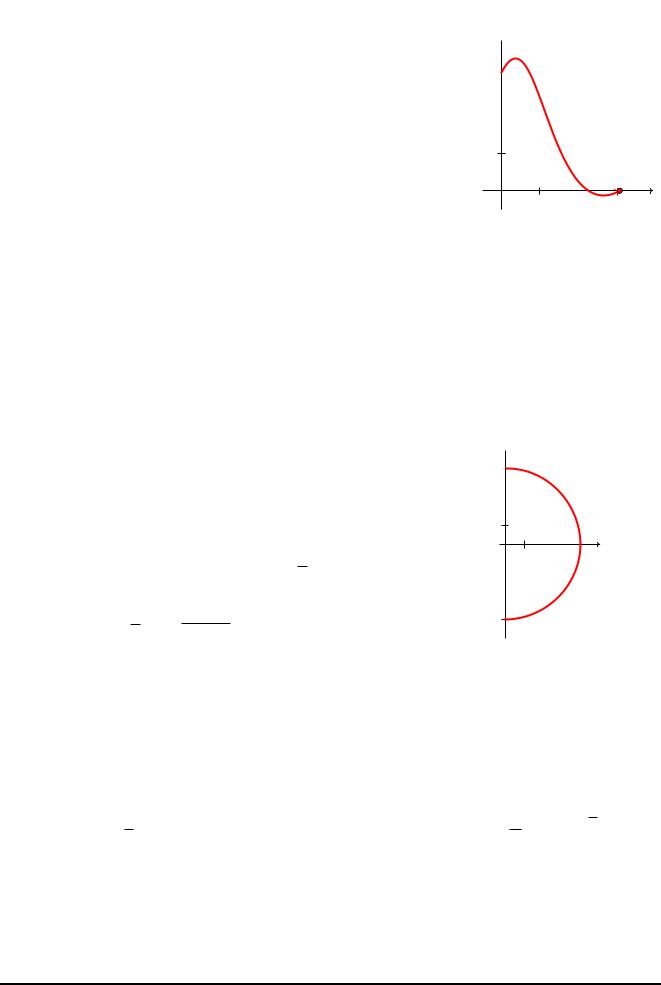
Приклад 8.4. C Обчислити iнтеграл

Ik = Z		z2 + sin2 z dz; k = 1; 2; 3;
k

якщо

а) 1 = fz : jzj = 1g ;

б) 2 — це вiдрiзок, який з’єднує точки z1 = 1 i z2 =

i;
в) 3 = nz : jzj = 1; arg z		o:
	2
B

		iy
	1	i
		z2
		2

z1

01 x

3

Рис. 11: До прикладу 8.4

Розв’язання. J Зауважимо, що пiдiнтегральна функцiя f(z) = z2 + sin2 z всюди є аналiтичною f 2 A (C) (див. задачу 179).

а) Оскiльки 1 — це замкнена крива, а пiдiнтегральна фукцiя є аналiтичною, то за iнтегральною теоремою Кошi, див. (8.7), випливає, що

I1 = Z

z2

+ sin2 z dz = 0:

1

б) Застосуємо формулу Ньютона—Лейбнiца (8.10):

I2 = Z

i

z2 + sin2 z

i

z2 + 1

2

dz =

z2 + sin2 z dz = Z

dz = Z

cos 2z

2

1

1

z3

z

sin 2

z

i

i

i

sin 2i

1

1

sin 2

=

+

=

+

+

=

3

2

4

1

3

2

4

3

2

4

=	5	+	sin 2			+ i	1			sh 2		:
	6		4				6			4

в) Кривi 2 i 3 мають однаковi початки i кiнцi, а пiдiнтегральна фукцiя є аналiтичною, тому iнтеграл не залежить вiд шляху iнтегрування, див. (8.9),

звiдки

= I2

= 6

+ 4

+ i

6

4

:

I3

5

sin 2

1

sh 2

I

Приклад 8.5. C Обчислити iнтеграл

I = Z

zezdz;

якщо — це деякий кусково-гладкий контур, який з’єднує точки z1 = i i z2 = . B

v. 25 березня 2014 р.	c
	Є. Д. Бiлоколос, Л. Д. Зайцева, Д. Д. Шека, 2014

Роздiл 8. Iнтеграл вiд функцiї комплексної змiнної

47

Розв’язання. J Зауважимо, що пiдiнтегральна функцiя f(z) = zez всюди є аналiтичною f 2 A (C), тому можна застосувати формулу (8.11) iнтегрування частинами:

ezdz =

I = Z zezdz = Z zezdz = (zez) i Z

i

i

i

z

= e

i e

e

= e

1 =

+ i e

i

= e ( 1) 1 + i :

iy

z1

i
		x
0	1	z2

I									Рис. 12: До прикладу 8.5
Приклад 8.6. C Обчислити iнтеграл					pz ;
			I = Z
					dz
якщо = njzj = 4;		arg z		o; за умови p4 = 2. B
	2		2

Розв’язання. J Параметризуємо аналогiчно (8.6):

= nz(t) = 4eit;	1t 2 h					;			io:
					2		12
Тодi dz = 4ieitdt;	p		=							; k = 0; 1:
				2ei(t+2 k)=2
		z

1

Пiдiнтегральна функцiя f(z) = pz є багатозначною. Iнтегрувати будемо ту вiтку, яка визначається умовою

p p

4 = 4ei 2 k = 2ei k = 2;

звiдки k = 1.

Обчислимо iнтеграл, див. (8.3):

iy

4i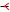

i
0 1	4 x

4i

Рис. 13: До прикладу 8.6

=2

=2

I = Z

dz

Z

eitdt

= 2ie i

Z

eit=2dt =

p

= 4i

2ei(t+2 )=2

z

=2

=2

i eit=2

= 2i

=2

= 4

ei =4 e i =4

= 4 2i sin 4 = 4p2i:

=2

2

I

Приклад 8.7. C Обчислити iнтеграл

Z

I = z2 Ln zdz;

c	v. 25 березня 2014 р.
Є. Д. Бiлоколос, Л. Д. Зайцева, Д. Д. Шека, 2014

48	Глава 2. Аналiтичнi функцiї. Iнтегрування функцiй комплексної змiнної

якщо = fz : jzj = 1g, за умови Ln( 1) = i : B Розв’язання. J Параметризуємо аналогiчно (8.6):

i

iy

= z(t) : z(t) = eit;

t 2 [ ; ] :

)

2 Z

Тодi

dz = ie

it

dt;

z

2

Ln z = e

2it

i (t + 2

k

; k

:

Пiдiнтегральна функцiя Ln z

є багатозначною. Iнте-

0

1 x

грувати будемо ту вiтку, яка визначається умовою

Ln( 1) = Ln ei( +2 k) = i( + 2 k) = i ;

тобто k = 1:

Рис. 14: До прикладу 8.7

Обчислимо iнтеграл, див. (8.3):

3it

3it

I = Z

z2 Ln zdz = Z

+ Z

(t 2 ) e3itdt = (t 2 )

e

e

dt =

3i

3i

1

e

3it

2

=

e

3i

+ 3 e

3i

+

=

3i

(3i)2

3i :

I

297. Обчислити iнтеграл

Ik = Z

(3z 2 Re z) dz;

k = 1; 2; 3;

k

якщо

а) 1 — це вiдрiзок, який з’єднує точки z1 = 1 i i z2 = 0;

б) 2 — це частина параболи, яка з’єднує точки z1

i z2; за умови, що

задана парабола має вершину в z2 i є симетричною вiдносно уявної

осi;

в) 3 — це ламана z1z3z2, де z3 = 1:

298. Обчислити iнтеграл

Ik = Z

(Im z z + 2z) dz;

k = 1; 2; 3; 4;

k

якщо

а) 1 — це вiдрiзок, який з’єднує точки z1 = 0 i z2 = 2i 3;

б) 2 — це частина параболи, яка з’єднує точки z1

i z2; за умови, що

задана парабола має вершину в z1 i є симетричною вiдносно уявної

осi;

v. 25 березня 2014 р.	c
	Є. Д. Бiлоколос, Л. Д. Зайцева, Д. Д. Шека, 2014

Роздiл 8.	Iнтеграл вiд функцiї комплексної змiнної					49
в)	3	— це ламана z1z3z2, де z3 = 3;
г) 4		— це ламана z1z4z2, де z4 = 2i:
299. Обчислити iнтеграл
		Ik = Z			3jzj2 + 1 dz;	k = 1; 2; 3;
якщо			k
а) 1		— це вiдрiзок, який з’єднує точки z1 = 0 i z2 = 1 + 2i;
б) 2		— це частина параболи, яка з’єднує точки z1 i z2; за умови, що
	задана парабола має вершину в z1 i є симетричною вiдносно дiйсної
	осi;
в) 3		— це ламана z1z3z2, де z3 = 2i:
300. Обчислити iнтеграл
		Ik = Z		z2	Re z + i dz;	k = 1; 2; 3;
якщо		k
а) 1		— це вiдрiзок, який з’єднує точки z1 = 1 i i z2 = 0;
б) 2		— це частина кубiчної параболи y = x3; яка з’єднує точки z1 i z2;
в) 3		— це ламана z1z3z2, де z3 = 1:

В прикладах 301–308 обчислити iнтеграл I вздовж кривої :

301.		R		2 2				: jzj = 2; 0 < arg z < g :
	I =		z5	jzj3z2		dz, якщо = fz
					2			p
302.	I =	R								< arg z < =2g :
			jzjz z z dz, якщо = fz					: jzj = 1=2;
303.		R
	I =		Re z + Im z				dz, якщо =	z : jzj = 2		:
304.		R						: jzj = 1; 2 =3 < arg z < =3g :
	I =	(Im z jzjz) dz, якщо = fz
305.	I =	sh zdz, якщо — це вiдрiзок, який з’єднує точки 2i та 2 :
1 2i:
		R	e2z+Im zdz, якщо — це вiдрiзок, який з’єднує точки 2i 1 та
306.	I =R
2i:	I =	R	z ch Re zdz, якщо — це вiдрiзок, який з’єднує точки 1 i та
307.
+ i :		R	Im z sin zdz,				якщо — це вiдрiзок, який з’єднує точки та
308.	I =

c	v. 25 березня 2014 р.
Є. Д. Бiлоколос, Л. Д. Зайцева, Д. Д. Шека, 2014

50 Глава 2. Аналiтичнi функцiї. Iнтегрування функцiй комплексної змiнної

В прикладах 309–312 обчислити iнтеграл першого роду I вздовж кривої

	:	R
	309.		Im z2 jdzj, якщо — це вiдрiзок, який з’єднує точки 4 та1 3i:
		I =
	i =2:
		R	sh z jdzj, якщо — це вiдрiзок, який з’єднує точки i =2 та
	310.	I =
	311.	R	3
		I =	Re z4 jdzj, якщо =		z : jzj = p5 2; 0 < arg z < =8			:
	312.	R	z jdzj, якщо = fz		: jzj = 1; =6 < arg z < =6g :
		I =
	313.	Обчислити iнтеграл
			Ik = Z	z cos z2dz; k = 1; 2; 3;
			k

якщо

p

а) 1 = z : jzj = 2 ;

б) 2 — це вiдрiзок, який з’єднує точки 1 i i 1 + i;

	p
в) 3 = z : jzj = 2; =4 < arg z < =4 :
314. Обчислити iнтеграл
	Ik = Z sh2 2zdz;			k = 1; 2; 3;
			k
якщо

а) 1 = fz : jzj = g ;

б) 2 — це вiдрiзок, який з’єднує точки i i ;

в) 3 = fz : jzj = ; 0 < arg z < =2g :

315. Обчислити iнтеграл

Z

Ik = (iz 2)15 dz; k = 1; 2; 3;

k

якщо

а) 1 — це прямокутник з вершинами в точках 1 + i; 1 i; 1 i; 1 + i;

б) 2 — це вiдрiзок, який з’єднує точки z1 = 1 i i z2 = i;

в) 3 — це ламана z1z3z2, де z3 = 1 + i:

v. 25 березня 2014 р.	c
	Є. Д. Бiлоколос, Л. Д. Зайцева, Д. Д. Шека, 2014