- •Билет 1.
- •Свойства равнобедренного треугольника
- •Теорема о свойстве медианы равнобедренного треугольника
- •Билет 2.
- •Теорема о геометрическом месте точек, равноудаленных от двух данных точек
- •Второй признак равенства треугольников
- •Третий признак равенства треугольников III
- •Билет 7.
- •Теоремы об углах, образованных двумя параллельными прямыми и секущей Рис.7.1
- •Билет 18.
- •Свойства параллелограмма
- •Билет 21. Теорема Менелая
- •Билет 22. Средняя линия треугольника
- •Второй признак подобия треугольников
- •Вывод формулы площади параллелограмма
- •Билет 34.
- •Вывод формулы площади трапеции
- •Теорема о четырех точках трапеции
- •Билет 38.
- •Свойства окружности Апполония
- •Билет 39. Теорема Чевы
Билет 1.
Треугольник называется равнобедренным, если у него две стороны равны. Эти стороны называются боковыми, а третья сторона – основанием.
Свойства равнобедренного треугольника
-
Углы при основании равны и являются острыми;
-
Медиана, проведенная к основанию, является биссектрисой и высотой.
Теорема о свойстве медианы равнобедренного треугольника
Определение: Медиана, проведенная к основанию, является биссектрисой и высотой.
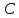
Доказательство:
Пусть Δ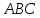 – равнобедренный, с основанием
– равнобедренный, с основанием
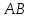 ,
и
,
и
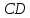 – медиана, проведенная к основанию. В
треугольниках
– медиана, проведенная к основанию. В
треугольниках
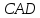 и
и
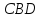 углы
углы
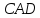 и
и
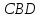 равны, как углы при основании
равнобедренного, стороны
равны, как углы при основании
равнобедренного, стороны
 и
и
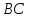 равны по определению равнобедренного
треугольника, стороны
равны по определению равнобедренного
треугольника, стороны
 и
и
 равны, потому что
равны, потому что
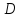 – середина отрезка
– середина отрезка
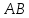 .
Отсюда получаем, что Δ
.
Отсюда получаем, что Δ Δ
Δ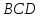 .
.
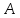
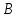
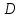




Билет 2.
Геометрическое место точек – это множество всех точек, удовлетворяющих определенным заданным условиям.
-
Срединный перпендикуляр любого отрезка есть геометрическое место точек, равноудаленных от концов этого отрезка.
-
Биссектриса угла есть геометрическое место точек, равноудаленных от его сторон.
-
Окружность есть геометрическое место точек, равноудаленных от ее центра.
Теорема о геометрическом месте точек, равноудаленных от двух данных точек
Определение:
Геометрическое место точек, равноудаленных
от двух данных точек, есть прямая,
перпендикулярная к отрезку, соединяющему
эти точки, и проходящая через его
середину.
Доказательство:
Пусть
 к
к
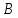 — данные точки,
— данные точки,
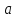 — прямая, проходящая через середину
— прямая, проходящая через середину
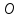 отрезка
отрезка
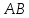 перпендикулярно к нему. Любая точка
перпендикулярно к нему. Любая точка
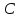 прямой
прямой
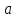 находится на одинаковом расстоянии от
точек
находится на одинаковом расстоянии от
точек
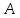 и
и
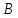 ,
следует из равенства треугольников
,
следует из равенства треугольников
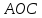 и
и
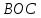 .
У этих треугольников углы при вершине
.
У этих треугольников углы при вершине
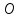 прямые, сторона
прямые, сторона
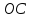 общая, а
общая, а
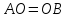 ,
так как
,
так как
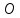 — середина отрезка
— середина отрезка
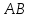 .
.


Билет 3.
Углы, смежные с углами треугольника, называются внешними углами треугольника.
Сумма
внешних углов многоугольника всегда
равна
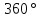 .
.
Теорема о внешнем угле треугольника
Определение: Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.


Доказательство:
Пусть Δ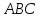 – данный треугольник. Из
теоремы о сумме углов треугольника,
– данный треугольник. Из
теоремы о сумме углов треугольника,
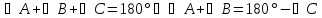 .
Но
.
Но
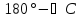 — величина внешнего угла при вершине
— величина внешнего угла при вершине
 ,
значит, внешний угол равен
,
значит, внешний угол равен
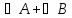 .
.
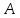
Билет 4.
Прямые, на всем своем протяжении не имеющие точек пересечения, называются параллельными.
Признаки параллельности прямых
-
Две прямые, параллельные третьей параллельны.
-
Если внутренние накрест лежащие* углы равны, то прямые параллельны.
-
Если сумма внутренних односторонних* углов равна 180°, то прямые параллельны.
-
Если соответственные* углы равны, то прямые параллельны.
*см. Билет 7.
Билет 5.
Соотношения между прямыми и отрезками окружности
-
Произведение отрезков пересекающихся хорд окружности равны.
-
Отрезки касательных, проведенные к окружности из одной точки равны.



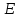

-
Квадрат отрезка касательной равен произведению отрезков секущей, проведенной из той же точки:
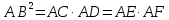
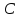
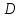

-
Произведения отрезков секущих, проведенных из одной точки, равны:

Билет 6.
I


Первый признак равенства треугольников
Определение:
Если две стороны и угол между ними
одного треугольника равны соответственно
двум сторонам и углу между ними другого
треугольника, то такие треугольники
равны.


Доказательство:
Рассмотрим Δ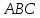 и Δ
и Δ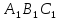 ,
у которого
,
у которого
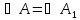 ,
,
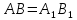 и
и
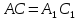 .
Так как
.
Так как
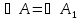 ,
то Δ
,
то Δ можно наложить на Δ
можно наложить на Δ так, что вершина
так, что вершина
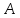 совместится с вершиной
совместится с вершиной
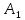 ,
а стороны
,
а стороны
 и
и
 наложатся соответственно на лучи
наложатся соответственно на лучи
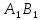 и
и
 .
Поскольку
.
Поскольку
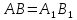 ,
,
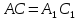 ,
то точка
,
то точка
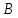 совместится с точкой
совместится с точкой
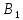 ,
а точка
,
а точка
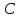 –
с точкой
–
с точкой
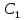 .
Итак, Δ
.
Итак, Δ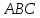 и Δ
и Δ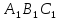 равны.
равны.
II