
- •Билет 1.
- •Свойства равнобедренного треугольника
- •Теорема о свойстве медианы равнобедренного треугольника
- •Билет 2.
- •Теорема о геометрическом месте точек, равноудаленных от двух данных точек
- •Второй признак равенства треугольников
- •Третий признак равенства треугольников III
- •Билет 7.
- •Теоремы об углах, образованных двумя параллельными прямыми и секущей Рис.7.1
- •Билет 18.
- •Свойства параллелограмма
- •Билет 21. Теорема Менелая
- •Билет 22. Средняя линия треугольника
- •Второй признак подобия треугольников
- •Вывод формулы площади параллелограмма
- •Билет 34.
- •Вывод формулы площади трапеции
- •Теорема о четырех точках трапеции
- •Билет 38.
- •Свойства окружности Апполония
- •Билет 39. Теорема Чевы
Второй признак подобия треугольников
Определение: Если две стороны одного треугольника пропорциональны двум сторонам другого и угол между этими
сторонами в первом и втором треугольнике равен, тогда эти треугольники подобны.
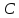
Доказательство:
Пусть стороны
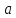 и
и
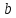 треугольника
треугольника
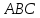 пропорциональны сторонам
пропорциональны сторонам
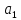 и
и
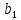 треугольника
треугольника
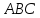 .
Преобразуем треугольник
.
Преобразуем треугольник
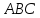 в подобный с коэффициентом подобия
в подобный с коэффициентом подобия
 .
Тогда у вновь полученного треугольника
.
Тогда у вновь полученного треугольника
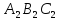 и треугольника
и треугольника
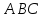 будут две пары равных сторон и равны
углы, заключенные между этими сторонами.
Треугольники
будут две пары равных сторон и равны
углы, заключенные между этими сторонами.
Треугольники
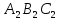 и
и
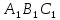 равны по признаку равенства
равны по признаку равенства 


треугольников, исходные же треугольники подобны.
Третий признак подобия треугольников
Определение: Если три стороны одного треугольника пропорциональны трем сходственным сторонам другого, то треугольники подобны.
Доказательство:
Пусть стороны треугольника
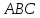 пропорциональны сходственным сторонам
треугольника
пропорциональны сходственным сторонам
треугольника
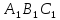 .
Преобразуем треугольник
.
Преобразуем треугольник
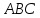 в подобный с коэффициентом подобия
в подобный с коэффициентом подобия
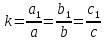 .
Получившийся треугольник и Δ
.
Получившийся треугольник и Δ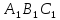 равны, из чего следует, что Δ
равны, из чего следует, что Δ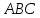 подобен Δ
подобен Δ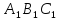 .
.
Билет 32.
Вывод формулы площади
треугольника
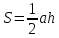 .
.
Дан
Δ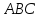 .
Достроим его до параллелограмма,
обозначив четвертую вершину точкой
.
Достроим его до параллелограмма,
обозначив четвертую вершину точкой
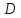 .
Треугольники равны по трем сторонам.
Значит, параллелограмм
.
Треугольники равны по трем сторонам.
Значит, параллелограмм
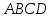 состоит из двух одинаковых треугольников.
Отсюда площадь одного из них равна
половине площади параллелограмма. Так
как площадь параллелограмма равна
состоит из двух одинаковых треугольников.
Отсюда площадь одного из них равна
половине площади параллелограмма. Так
как площадь параллелограмма равна
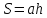 ,
то площадь прямоугольника
,
то площадь прямоугольника
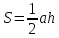 .
.
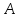
Вывод формулы Герона
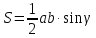 ,
где
,
где
 – угол, противолежащий стороне
– угол, противолежащий стороне
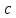 .
По теореме косинусов:
.
По теореме косинусов:
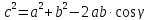 .
Отсюда:
.
Отсюда:
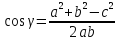 .
Значит:
.
Значит:

Замечая,
что
 ,
,
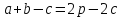 ,
,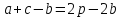 ,
,
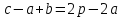 ,
получаем:
,
получаем:
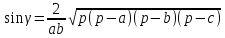 .
Отсюда
.
Отсюда
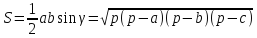 ,
ч. т. д.
,
ч. т. д.
Билет 33.
Вывод формулы площади
параллелограмма
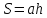
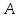
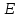

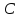
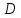
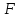
Пусть
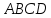 – данный параллелограмм. Опустим
перпендикуляр
– данный параллелограмм. Опустим
перпендикуляр
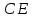 на прямую
на прямую
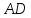 .
Тогда площадь трапеции
.
Тогда площадь трапеции
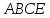 равна сумме площадей параллелограмма
равна сумме площадей параллелограмма
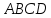 и треугольника
и треугольника
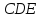 .
.
Опустим
перпендикуляр
 на прямую
на прямую
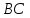 .
Тогда площадь трапеции
.
Тогда площадь трапеции
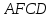 равна сумме площадей параллелограмма
равна сумме площадей параллелограмма
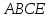 и треугольника
и треугольника
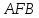 .
.
Треугольники
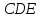 и
и
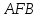 равны, значит, имеют равную площадь,
отсюда следует, что площадь параллелограмма
равна площади прямоугольника
равны, значит, имеют равную площадь,
отсюда следует, что площадь параллелограмма
равна площади прямоугольника
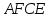 ,
значит, она равна
,
значит, она равна
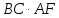 ,
где
,
где
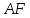 – высота данного параллелограмма.
– высота данного параллелограмма.
Вывод формулы площади параллелограмма
Пусть
в данном произвольном параллелограмме
диагонали равны
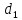 и
и
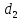 ,
а угол между ними –
,
а угол между ними –
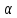 .
Так как диагонали параллелограмма
точкой пересечения делятся пополам, то
очевидно, что параллелограмм состоит
из четырех треугольников со сторонами
.
Так как диагонали параллелограмма
точкой пересечения делятся пополам, то
очевидно, что параллелограмм состоит
из четырех треугольников со сторонами
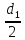 и
и
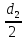 .
Площадь этого параллелограмма может
быть вычислена как сумма площадей данных
треугольников. Так как площадь
прямоугольника равна
.
Площадь этого параллелограмма может
быть вычислена как сумма площадей данных
треугольников. Так как площадь
прямоугольника равна
 ,
то площадь параллелограмма равна
,
то площадь параллелограмма равна
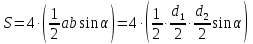 =
=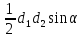 ,
что и требовалось доказать.
,
что и требовалось доказать.
Билет 34.
Трапеция – четырехугольник, у которого только одна пара противолежащих сторон параллельна.
Вывод формулы площади трапеции
Пусть
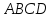 – данная трапеция. Диагональ
– данная трапеция. Диагональ
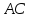 разбивает ее на два данных треугольника:
разбивает ее на два данных треугольника:
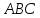 и
и
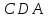 .
Следовательно, площадь трапеции равна
сумме их площадей. Высоты
.
Следовательно, площадь трапеции равна
сумме их площадей. Высоты
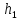 и
и
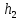 этих треугольников равны расстоянию
между параллельными прямыми
этих треугольников равны расстоянию
между параллельными прямыми
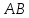 и
и
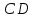 .
Отсюда,
.
Отсюда,
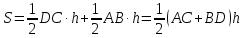
Теорема о четырех точках трапеции
Определение: В трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжений боковых сторон располагаются на одной прямой.
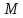
Доказательство:
Для этого докажем, что прямая, проходящая
через точку пересечения диагоналей
трапеции и через точку пересечения
продолжений ее боковых сторон, делит
основания трапеции пополам.
Обозначим
через
 и
и
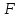 середины оснований
середины оснований
 и
и
 трапеции
трапеции
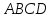 ;
;
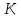 – точка пересечения ее диагоналей,
– точка пересечения ее диагоналей,
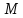 – точка пересечения продолжений боковых
сторон.
Заметим, что точки
– точка пересечения продолжений боковых
сторон.
Заметим, что точки
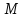 ,
,
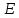 и
и
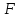 лежат на одной прямой. Это следует из
подобия треугольников
лежат на одной прямой. Это следует из
подобия треугольников
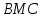 и
и
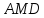 .
В каждом из них отрезки
.
В каждом из них отрезки
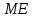 и
и
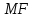 соответственно являются медианами, а
значит, они делят угол при вершине
соответственно являются медианами, а
значит, они делят угол при вершине
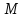 на одинаковые части.
Точно так же на
одной прямой расположены точки
на одинаковые части.
Точно так же на
одной прямой расположены точки
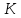 ,
,
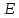 и
и
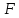 .
(Здесь это следует из подобия треугольников
.
(Здесь это следует из подобия треугольников
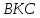 и
и
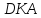 .)
Значит, все четыре токи
.)
Значит, все четыре токи
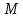 ,
,
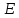 ,
,
 и
и
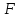 лежат на одной прямой, т.е. прямая
лежат на одной прямой, т.е. прямая
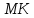 проходит через
проходит через
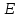 и
и
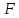 .
.






Билет 35.
Теорема Пифагора

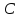
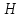
Определение: Квадрат длины гипотенузы прямоугольного треугольника равен сумме квадратов длин его катетов.
Доказательство:
Проведем высоту BH из
угла B к стороне AC.
Δ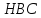 подобен Δ
подобен Δ по двум углам. Аналогично, Δ
по двум углам. Аналогично, Δ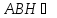 Δ
Δ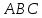 .
Отсюда:
.
Отсюда:
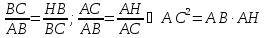 .
Теорема доказана.
.
Теорема доказана.
Билет 36.
Теорема синусов
Определение: Стороны треугольника пропорциональны синусам противолежащих углов.
Доказательство:
Пусть дан треугольник со сторонами
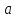 ,
,
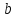 и
и
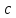 .
Его площадь можно найти по формуле:
.
Его площадь можно найти по формуле:
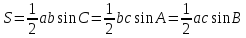 .
Из первых двух выражений получаем:
.
Из первых двух выражений получаем:
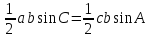 .
Отсюда,
.
Отсюда,
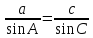 .
Аналогично,
.
Аналогично,
 .
Следовательно,
.
Следовательно,
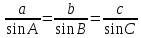 .
Теорема доказана.
.
Теорема доказана.
Билет 37.
Теорема косинусов
Определение:
Квадрат стороны треугольника равен
сумме квадратов других сторон треугольника,
минус удвоенное произведение этих
сторон на косинус угла между ними.
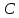
Доказательство:
Рассмотрим треугольник
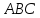 .
Из вершины
.
Из вершины
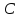 на сторону
на сторону
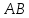 опущена высота
опущена высота
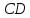 .
Из треугольника
.
Из треугольника
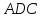 следует, что
следует, что
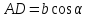 и
и
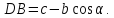 Запишем теорему Пифагора для двух
прямоугольных треугольников
Запишем теорему Пифагора для двух
прямоугольных треугольников
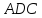 и
и
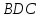 :
:
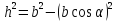 (1)
(1)
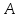
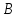

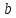
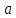

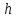
 (2)
(2)
Приравниваем правые части уравнений (1) и (2):
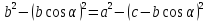 ,
или
,
или
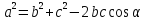 .Аналогично,
.Аналогично,
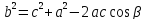 ,
и
,
и
 .
.
