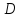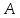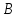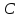- •Билет 1.
- •Свойства равнобедренного треугольника
- •Теорема о свойстве медианы равнобедренного треугольника
- •Билет 2.
- •Теорема о геометрическом месте точек, равноудаленных от двух данных точек
- •Второй признак равенства треугольников
- •Третий признак равенства треугольников III
- •Билет 7.
- •Теоремы об углах, образованных двумя параллельными прямыми и секущей Рис.7.1
- •Билет 18.
- •Свойства параллелограмма
- •Билет 21. Теорема Менелая
- •Билет 22. Средняя линия треугольника
- •Второй признак подобия треугольников
- •Вывод формулы площади параллелограмма
- •Билет 34.
- •Вывод формулы площади трапеции
- •Теорема о четырех точках трапеции
- •Билет 38.
- •Свойства окружности Апполония
- •Билет 39. Теорема Чевы
Второй признак равенства треугольников
Определение: Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.
Доказательство:
Рассмотрим Δ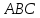 и Δ
и Δ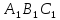 ,
где
,
где
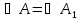 ,
,
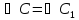 и
и
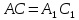 .
Треугольники подобны по двум углам
(
.
Треугольники подобны по двум углам
( ,
,
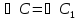 ).
Более того, их коэффициент подобия
).
Более того, их коэффициент подобия
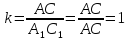 ,
следовательно, они равны.
,
следовательно, они равны.
Третий признак равенства треугольников III
Определение: Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.
Доказательство:
Рассмотрим Δ и Δ
и Δ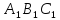 такие, что
такие, что
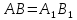 ,
,
 ,
а
,
а
 .
Они подобны по третьему признаку
подобия треугольников**. Так как стороны
не только пропорциональны, но и равны,
то коэффициент подобия
.
Они подобны по третьему признаку
подобия треугольников**. Так как стороны
не только пропорциональны, но и равны,
то коэффициент подобия
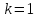 .
Следовательно, Δ
.
Следовательно, Δ и Δ
и Δ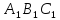 равны.
равны.
** см. Билет 31.
Билет 7.
На чертеже:
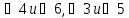 – накрест
лежащие;
– накрест
лежащие;
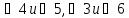 – односторонние;
– односторонние;
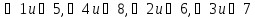 – соответственные.
– соответственные.
Теоремы об углах, образованных двумя параллельными прямыми и секущей Рис.7.1
Теорема: Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
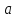
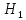

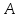
Доказательство:
Пусть
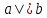 ,
и секущая
,
и секущая
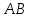 ,
пересекающая их, образует накрест
лежащие углы
,
пересекающая их, образует накрест
лежащие углы
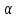 и
и
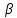 .
Проведем перпендикуляр из точки
.
Проведем перпендикуляр из точки
 к прямой
к прямой
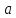 и из точки
и из точки
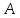 к прямой
к прямой
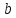 .
Данные треугольники будут равны по углу
и двум сторонам (
.
Данные треугольники будут равны по углу
и двум сторонам (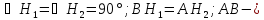 общ.),
отсюда
общ.),
отсюда
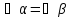 .
.

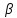


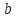

Теорема: Если две параллельные прямые пересечены секущей, то соответственные углы равны.
Доказательство:
Обратимся к рис.7.1.
Докажем, что соответственные углы,
 к
примеру, равны. Так как углы
к
примеру, равны. Так как углы
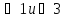 – вертикальные, то
– вертикальные, то
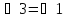 .
Углы
.
Углы
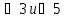 равны как накрест лежащие, следовательно,
равны как накрест лежащие, следовательно,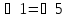 .
.
Теорема:
Если две параллельные прямые пересечены
секущей, сумма односторонних углов
равна
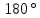 .
.
Доказательство:
Обратимся к рис.7.1.
Докажем, что сумма односторонних углов,
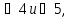 к
примеру, равна
к
примеру, равна
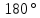 .
Углы
.
Углы
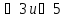 равны как накрест лежащие. Углы
равны как накрест лежащие. Углы
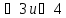 смежные, поэтому их сумма равна
смежные, поэтому их сумма равна
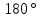 .
Но
.
Но
 ,
следовательно,
,
следовательно,
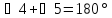 ,
что и требовалось доказать.
,
что и требовалось доказать.
Билет 8.
Часть плоскости, ограниченная окружностью, называется кругом.
Площадь
круга:
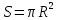
Площадь кругового сектора
Так
как площадь круга равна
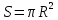 ,
то площадь кругового сектора ограниченного
дугой в
,
то площадь кругового сектора ограниченного
дугой в
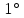 равна
равна
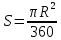 .
Отсюда площадь сектора, ограниченного
дугой в
.
Отсюда площадь сектора, ограниченного
дугой в
 градусов:
градусов:
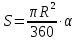 .
.
Билет 9.
Нахождение значений
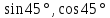 ,
и
,
и
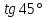






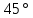
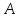
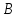
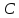
Пусть
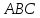 – равнобедренный прямоугольный
треугольник.
– равнобедренный прямоугольный
треугольник.
Выразим
гипотенузу
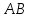 через
катеты по теореме Пифагора:
через
катеты по теореме Пифагора:
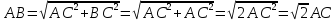 .
.
Т. к. синус – отношение противолежащего катета к гипотенузе, то:
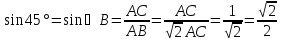
Аналогично,
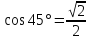 .
.

Билет 10.
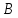
Вывод формулы площади
треугольника


За
основу возьмем формулу площади
треугольника
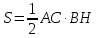 *.
*.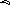
Так как синус по определению – это отношение противолежащего
катета
к гипотенузе, то
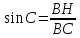 .
Отсюда,
.
Отсюда,
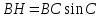 .
.

Подставив
в исходную формулу, получаем:
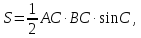
иными
словами,
 ,
что и требовалось доказать.
,
что и требовалось доказать.
*см. Билет 32.
Билет 11.
Нахождение гипотенузы, катета
и острого угла прямоугольного треугольника
по данным его второго катета и острому
углу
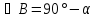 (по
теореме о сумме углов треугольника**)
(по
теореме о сумме углов треугольника**)
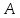
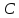
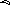
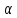
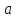
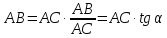

** см. Билет 15.
Билет 12.
Теорема о сумме углов выпуклого многоугольника
Определение:
Сумма углов n-угольника
равна
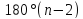
Доказательство:
Пусть
 —
данный выпуклый многоугольник, и
—
данный выпуклый многоугольник, и
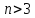 .
Тогда проведем из одной вершины к
противоположным вершинам
.
Тогда проведем из одной вершины к
противоположным вершинам
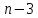 диагонали:
диагонали:
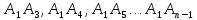 .
Так как многоугольник выпуклый, то эти
диагонали разбивают его на
.
Так как многоугольник выпуклый, то эти
диагонали разбивают его на
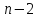 треугольника: Δ
треугольника: Δ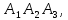 Δ
Δ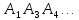 Δ
Δ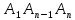 .
Сумма углов многоугольника совпадает
с суммой углов всех этих треугольников.
Сумма углов в каждом треугольнике равна
180°, а число этих треугольников есть
.
Сумма углов многоугольника совпадает
с суммой углов всех этих треугольников.
Сумма углов в каждом треугольнике равна
180°, а число этих треугольников есть
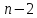 .
Следовательно, сумма углов n-угольника
равна
.
Следовательно, сумма углов n-угольника
равна
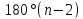 .
Теорема доказана.
.
Теорема доказана.
Билет 13.
Деление отрезка на
 равных частей
равных частей
Пусть
 – данный отрезок. Проведем из точки
– данный отрезок. Проведем из точки
 луч
луч
 ,
не содержащий отрезок
,
не содержащий отрезок
 .
Отложим от точки
.
Отложим от точки
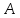 на построенном луче равные отрезки:
на построенном луче равные отрезки:
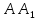 ,
, 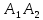
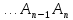 .
Соединим точки
.
Соединим точки
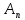 и
и
 .
Проведем через точки
.
Проведем через точки
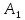 ,
, 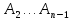 прямые, параллельные* прямой
прямые, параллельные* прямой
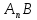 .
Они пересекают отрезок
.
Они пересекают отрезок
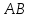 в точках
в точках
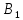 ,
, 

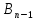 .
Отрезки
.
Отрезки
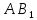 ,
, 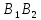
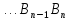 – искомые отрезки.
– искомые отрезки.
* см. Билет 45.
Билет 14.
Зависимость между стороной правильного n-угольника и радиусом описанной и вписанной окружности
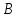
Рассмотрим
рис.14.1.
В прямоугольном треугольнике Δ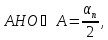 где
где
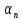 – величина угла правильного n-угольника.
Эту величину можно найти по формуле
– величина угла правильного n-угольника.
Эту величину можно найти по формуле
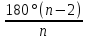 (следствие из теоремы о сумме углов
многоугольника**). Отсюда
(следствие из теоремы о сумме углов
многоугольника**). Отсюда
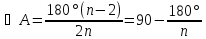 .
Тогда сторона
.
Тогда сторона
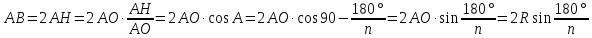 ;
а
;
а
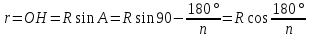 .
Из
последней формулы выразим
.
Из
последней формулы выразим
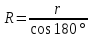 .
Подставим вместо
.
Подставим вместо
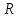 получившееся выражение:
получившееся выражение:
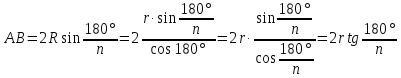 .
.
Рис.14.1
Рассмотрим несколько частных случаев:
Для
равностороннего треугольника:
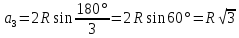
Для
квадрата:
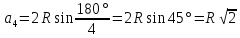
Для
правильного шестиугольника:
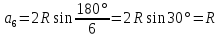
** см. Билет 12.
Билет 15.
Треугольником называется фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки.
Теорема о сумме углов треугольника


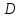



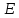
Определение:
Сумма углов треугольника равна
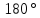 .
.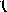

Доказательство:
Рассмотрим рис.15.1.
Углы
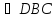 и
и
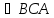 равны как накрест лежащие. Аналогично,
равны как накрест лежащие. Аналогично,
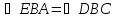 .
Но углы
.
Но углы
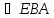 ,
,
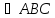 и
и
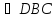 образуют развернутый угол, следовательно,
их сумма равна
образуют развернутый угол, следовательно,
их сумма равна
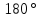 .
тогда сумма соответствующих углов
треугольника также равна
.
тогда сумма соответствующих углов
треугольника также равна
 ,
ч. т. д.
,
ч. т. д.
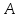

Рис.15.1
Билет 16.
Признаки равенства прямоугольных треугольников
См. Билет 6.
Примечание: при доказательстве признаков равенства прямоугольных треугольников следует принимать во внимание, что один прямой угол у них итак равен.
Билет 17.
Признаки параллелограмма
-
Если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм. Доказательство: Пусть
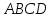 – данный четырехугольник,
– данный четырехугольник,
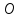 – точка пересечения диагоналей данного
параллелограмма.
Δ
– точка пересечения диагоналей данного
параллелограмма.
Δ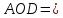 Δ
Δ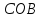 по первому признаку равенства
треугольников (
по первому признаку равенства
треугольников (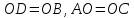 по
условию теоремы,
по
условию теоремы,
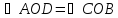 ,
как вертикальные углы). Следовательно,
,
как вертикальные углы). Следовательно,
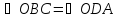 .
А они являются внутренними накрест
лежащими для прямых
.
А они являются внутренними накрест
лежащими для прямых
 и
и
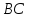 и секущей
и секущей
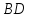 .
По признаку параллельности прямых
прямые
.
По признаку параллельности прямых
прямые
 и
и
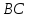 параллельны. Так же доказываем, что
параллельны. Так же доказываем, что
 и
и
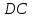 тоже параллельны. По определению данный
четырехугольник параллелограмм. Теорема
доказана.
тоже параллельны. По определению данный
четырехугольник параллелограмм. Теорема
доказана.
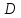







-
Если у четырехугольника пара противоположных сторон параллельны и равны, то четырехугольник – параллелограмм. Доказательство: Пусть
 – данный четырехугольник.
– данный четырехугольник.
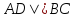 и
и
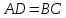 .
Тогда Δ
.
Тогда Δ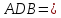 Δ
Δ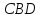 по первому признаку равенства
треугольников (
по первому признаку равенства
треугольников (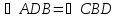 ,
как внутренние накрест лежащие между
прямыми
,
как внутренние накрест лежащие между
прямыми
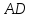 и
и
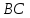 и секущей
и секущей
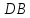 ,
,
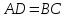 по условию,
по условию,
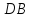 – общая).
Следовательно,
– общая).
Следовательно,
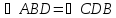 ,
а эти углы являются внутренними накрест
лежащими для прямых
,
а эти углы являются внутренними накрест
лежащими для прямых
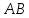 и
и
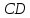 и секущей
и секущей
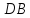 .
По теореме признаке параллельности
прямых
.
По теореме признаке параллельности
прямых
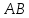 и
и
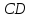 параллельны. Значит,
параллельны. Значит,
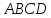 – параллелограмм. Теорема доказана.
– параллелограмм. Теорема доказана.
-
Если в четырехугольнике противолежащие углы равны, такой четырехугольник – параллелограмм. Доказательство: Пусть дан четырехугольник
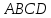 .
.
 и
и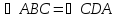 .
Проведем диагональ DB. Сумма углов
четырех угольника равна сумме углов
треугольников
.
Проведем диагональ DB. Сумма углов
четырех угольника равна сумме углов
треугольников
 и
и
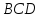 .
По теореме о сумме углов треугольника,
получаем:
.
По теореме о сумме углов треугольника,
получаем:
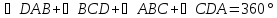 .
Так как противолежащие углы в
четырехугольнике равны, то
.
Так как противолежащие углы в
четырехугольнике равны, то
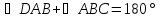 и
и
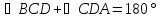 .
Углы
.
Углы
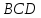 и
и
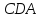 являются внутренними односторонними
для прямых
являются внутренними односторонними
для прямых
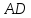 и
и
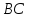 и секущей
и секущей
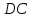 ,
их сумма равна
,
их сумма равна
 ,
поэтому из следствия к теореме о признаке
параллельности прямых, прямые
,
поэтому из следствия к теореме о признаке
параллельности прямых, прямые
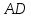 и
и
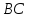 параллельны. Так же доказывается, что
параллельны. Так же доказывается, что
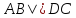 .
Таким образом, четырехугольник
.
Таким образом, четырехугольник
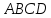 – параллелограмм по определению.
Теорема доказана.
– параллелограмм по определению.
Теорема доказана.