
- •Билет 1.
- •Свойства равнобедренного треугольника
- •Теорема о свойстве медианы равнобедренного треугольника
- •Билет 2.
- •Теорема о геометрическом месте точек, равноудаленных от двух данных точек
- •Второй признак равенства треугольников
- •Третий признак равенства треугольников III
- •Билет 7.
- •Теоремы об углах, образованных двумя параллельными прямыми и секущей Рис.7.1
- •Билет 18.
- •Свойства параллелограмма
- •Билет 21. Теорема Менелая
- •Билет 22. Средняя линия треугольника
- •Второй признак подобия треугольников
- •Вывод формулы площади параллелограмма
- •Билет 34.
- •Вывод формулы площади трапеции
- •Теорема о четырех точках трапеции
- •Билет 38.
- •Свойства окружности Апполония
- •Билет 39. Теорема Чевы
Билет 18.
Параллелограммом называется четырехугольник, у которого противолежащие стороны попарно параллельны.
Свойства параллелограмма
-
В параллелограмме противоположные стороны равны. Доказательство: Пусть
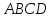 – параллелограмм. Диагональ
– параллелограмм. Диагональ
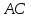 делит
его на два треугольника: Δ
делит
его на два треугольника: Δ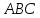 и
Δ
и
Δ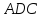 .
Эти треугольники равны по стороне и
двум углам (
.
Эти треугольники равны по стороне и
двум углам (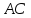 – общая,
– общая,
 ,
,
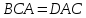 – как накрест лежащие). Отсюда,
– как накрест лежащие). Отсюда,
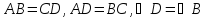 .
Теорема доказана.
.
Теорема доказана.
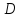
-
В параллелограмме противоположные углы равны. Доказательство: аналогично свойству I.
-
Диагонали параллелограмма точкой пересечения делятся пополам. Доказательство: Пусть
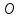 – точка пересечения диагоналей
параллелограмма ABCD. Δ
– точка пересечения диагоналей
параллелограмма ABCD. Δ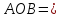 Δ
Δ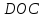 по стороне и двум углам (
по стороне и двум углам (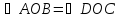 как вертикал.,
как вертикал.,
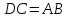 ,
,
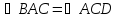 как накрест лежащие). Отсюда
как накрест лежащие). Отсюда
 ,
,
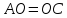 ,
ч. т. д.
,
ч. т. д.
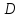








Билет 19.
Прямоугольником называют параллелограмм, у которого все углы прямые
Особое свойство прямоугольника
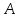
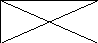
Диагонали
прямоугольника равны.
Доказательство:
Рассмотрим прямоугольник
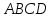 .
Δ
.
Δ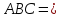 Δ
Δ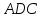 по двум катетам. Отсюда диагонали
по двум катетам. Отсюда диагонали
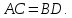 Обратное
утверждение (признак): Если в параллелограмме
диагонали равны, то этот параллелограмм
является прямоугольником.
Обратное
утверждение (признак): Если в параллелограмме
диагонали равны, то этот параллелограмм
является прямоугольником.

Билет 20.
Ромбом называется параллелограмм, у которого все стороны равны.
Особое свойство ромба
Диагонали
ромба пересекаются под прямым углом и
делят его углы пополам.
Доказательство:
Рассмотрим ромб
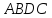 ,
требуется доказать, что
,
требуется доказать, что
 ,
и что диагонали ромба делят его углы
пополам. Докажем, например, что
,
и что диагонали ромба делят его углы
пополам. Докажем, например, что
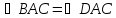 .
Т. к.
.
Т. к.
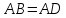 ,
то Δ
,
то Δ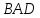 – равнобедренный. Так как ромб –
параллелограмм, то точкой пресечения
его диагонали делятся пополам, значит
– равнобедренный. Так как ромб –
параллелограмм, то точкой пресечения
его диагонали делятся пополам, значит
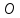 – медиана равнобедренного треугольника
– медиана равнобедренного треугольника
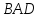 ,
а значит его биссектриса и высота.
Поэтому
,
а значит его биссектриса и высота.
Поэтому
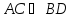 и
и
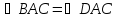 .
.
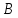
Билет 21. Теорема Менелая
Определение:
Если точки
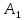 ,
,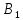 ,
, лежат соответственно на сторонах
лежат соответственно на сторонах
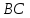 ,
,
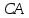 и
и
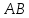 треугольника Δ
треугольника Δ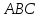 или на их продолжениях, то они лежат на
одной прямой тогда и только тогда, когда
или на их продолжениях, то они лежат на
одной прямой тогда и только тогда, когда
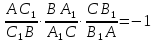 .
.
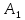

Доказательство:
Проведем через точку
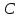 прямую, параллельную прямой
прямую, параллельную прямой
 ,
и обозначим через
,
и обозначим через
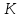 точку пересечения этой прямой с прямой
точку пересечения этой прямой с прямой
 .
Поскольку Δ
.
Поскольку Δ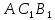 подобен Δ
подобен Δ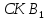 (по двум углам), тогда
(по двум углам), тогда
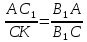 .
Так как подобными так же являются Δ
.
Так как подобными так же являются Δ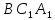 и Δ
и Δ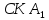 ,
то
,
то
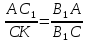 .
Выразив
.
Выразив
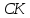 из второй формулы и подставив в первую,
получаем:
из второй формулы и подставив в первую,
получаем:
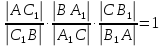 .
Остается заметить, что возможны два
расположения точек
.
Остается заметить, что возможны два
расположения точек
 ,
,
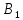 и
и
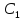 :
либо две из них лежат на соответствующих
сторонах треугольника, а третья — на
продолжении, либо все три лежат на
продолжениях соответствующих сторон.
Отсюда для отношений направленных
отрезков имеем:
:
либо две из них лежат на соответствующих
сторонах треугольника, а третья — на
продолжении, либо все три лежат на
продолжениях соответствующих сторон.
Отсюда для отношений направленных
отрезков имеем:
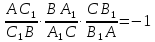 ,
что и требовалось доказать.
,
что и требовалось доказать.
Билет 22. Средняя линия треугольника
Средняя линия треугольника – отрезок, соединяющий середины двух сторон этого треугольника. Обладает следующими свойствами:
-
Средняя линия треугольника, соединяющая середины двух сторон, параллельна третьей стороне и равна ее половине.
-
При проведении всех трех средних линий образуются 4 равных треугольника, подобных исходному с коэффициентом 0,5.
-
Средняя линия отсекает треугольник, который подобен данному, а его площадь равна одной четверти площади исходного треугольника.
Средняя линия трапеции
Средняя линия трапеции — отрезок, соединяющий середины боковых сторон этой трапеции. Обладает следующими свойствами:
-
средняя линия параллельна основаниям трапеции и равна их полусумме;
-
середины сторон равнобедренной трапеции являются вершинами ромба.
Билет 23.
Расстояние между двумя точками на плоскости
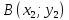
Определение:
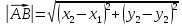
Доказательство:
Расстояние между началом координат и заданной точкой:
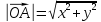
Билет 24.
Окружностью называется геометрическое место точек,
равноудаленных от заданной.
Длина
окружности:
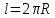
Длина дуги окружности
Так
как длина окружности равна
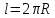 ,
то длина дуги в
,
то длина дуги в
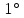 равна
равна
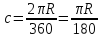 .
Отсюда дуги в
.
Отсюда дуги в
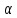 градусов:
градусов:
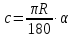 .
.
Билет 25.
Построение треугольника по трем элементам
Задача:
Построить
треугольник с данными сторонами

Решение:
Проведем луч и на нем
отложим отрезок
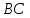 ,
равный
,
равный
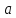 .
Раствором циркуля, равным
.
Раствором циркуля, равным
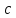 ,
проведем дугу с центром в точке
,
проведем дугу с центром в точке
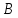 .
Далее раствором циркуля, равным
.
Далее раствором циркуля, равным
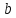 ,
проведем вторую дугу с центром в точке
,
проведем вторую дугу с центром в точке
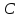 .
Пусть
.
Пусть
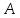 – точка пересечения этих дуг. Соединив
точку
– точка пересечения этих дуг. Соединив
точку
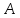 с точками
с точками
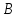 и
и
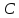 получим треугольник
получим треугольник
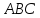 .
Это и есть искомый треугольник, так как
стороны равны данным отрезкам:
.
Это и есть искомый треугольник, так как
стороны равны данным отрезкам:
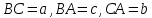 .
Задача:
Построить
треугольник по двум сторонам и углу
между ними.
.
Задача:
Построить
треугольник по двум сторонам и углу
между ними.
Решение:
Пусть даны
отрезки
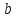 ,
,
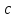 и угол
и угол
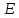 .
Построим угол
.
Построим угол
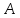 ,
равный углу
,
равный углу
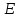 .
С помощью циркуля на сторонах угла
.
С помощью циркуля на сторонах угла
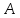 отложим отрезок
отложим отрезок
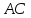 ,
равный
,
равный
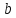 ,
и отрезок
,
и отрезок
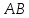 ,
равный
,
равный
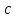 .
Соединив точки
.
Соединив точки
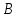 ,
,
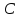 получим искомый треугольник
получим искомый треугольник
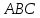 .
.
Задача: Построить треугольник по стороне и двум прилежащим углам.
Решение:
Пусть даны два
угла с вершинами
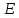 ,
,
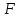 и отрезок
и отрезок
 .
Проведем прямую
.
Проведем прямую
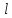 и на ней отложим отрезок
и на ней отложим отрезок
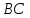 ,
равный отрезку
,
равный отрезку
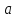 .
На одной из полуплоскостей построим
два угла. Один из этих углов равен углу
.
На одной из полуплоскостей построим
два угла. Один из этих углов равен углу
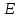 и сторона угла сонаправлена с лучом
и сторона угла сонаправлена с лучом
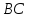 ,
и соответственно второй угол равен углу
,
и соответственно второй угол равен углу
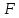 и сторона угла сонаправлена с лучом
и сторона угла сонаправлена с лучом
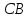 .
Вторые стороны этих углов пересекаются
в точке
.
Вторые стороны этих углов пересекаются
в точке
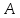 .
Полученный треугольник
.
Полученный треугольник
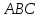 – искомый треугольник.
– искомый треугольник.
Билет 26.
Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне этого треугольника.
Свойства биссектрис треугольника
-
Биссектриса угла — это геометрическое место точек, равноудаленных от сторон этого угла.
-
Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам.
-
Точка пересечения биссектрис треугольника является центром окружности, вписанной в этот треугольник.
Построение биссектрисы угла
Из
вершины
 данного угла, как из центра, опишем
окружность произвольного радиуса. Пусть
данного угла, как из центра, опишем
окружность произвольного радиуса. Пусть
 и
и
 – точки пересечения ее со сторонами
угла. Построим еще две окружности с тем
же радиусом с центрами в
– точки пересечения ее со сторонами
угла. Построим еще две окружности с тем
же радиусом с центрами в
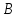 и
и
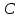 .
Пусть
.
Пусть
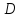 – точка их пересечения. Тогда
– точка их пересечения. Тогда
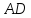 – искомая биссектриса угла
– искомая биссектриса угла
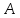 .
.
Билет 27.
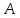
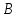

Нахождение катета и острых углов прямоугольного треугольника по данным его гипотенузы и другого катета
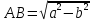
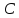
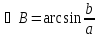
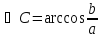
Билет 28.
Построение прямой проходящей через данную точку и перпендикулярной данной прямой
Проведем
окружность произвольного радиуса с
центром в данной точке
 .
Пусть
.
Пусть
 и
и
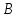 – точки пересечения этой окружности
данной прямой
– точки пересечения этой окружности
данной прямой
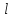 .
Из точек
.
Из точек
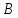 и
и
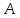 радиусом
радиусом
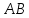 проведем окружность, точку пересечения
этих двух окружностей обозначим через
проведем окружность, точку пересечения
этих двух окружностей обозначим через
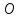 .
Проведем прямую
.
Проведем прямую
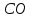 .
Перпендикулярность прямых
.
Перпендикулярность прямых
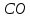 и
и
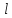 следует из равенства треугольников
следует из равенства треугольников
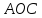 и
и
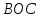 .
.
Билет 29.
Четырехугольник, все вершины которого лежат на окружности, называется вписанным.
Свойства вписанного четырехугольника
-
Сумма противоположных углов вписанного четырехугольника равна 180°.
-
Произведение диагоналей вписанного четырехугольника равно сумме произведений противоположных сторон (теорема Птолемея).
-
Площадь
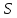 вписанного четырехугольника со сторонами
вписанного четырехугольника со сторонами
 можно вычислить по формулам:
можно вычислить по формулам:
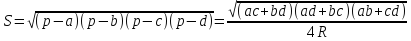 ,
где
,
где
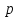 – полупериметр,
– полупериметр,
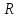 – радиус окружности.
– радиус окружности. -
Диагонали вписанного четырехугольника равны:
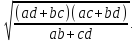
Билет 30.
Построение окружности вписанной в треугольник
Построим
биссектрисы хотя бы двух углов
треугольника*. Из точки пересечения
биссектрис
 проведем перпендикуляр**
проведем перпендикуляр** к любой из сторон треугольника. Тогда
центр вписанной окружности будет лежать
в точке пересечения биссектрис
к любой из сторон треугольника. Тогда
центр вписанной окружности будет лежать
в точке пересечения биссектрис
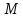 ,
а радиус этой окружности будет равен
расстоянию от этой точки к стороне
треугольника, то есть
,
а радиус этой окружности будет равен
расстоянию от этой точки к стороне
треугольника, то есть
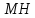 .
.
* см. Билет 26. ** см. Билет 28.
Построение окружности описанной вокруг треугольника
Найдем середины хотя бы двух сторон треугольника***. Из точек, являющихся серединами этих сторон, проведем перпендикуляры**. Точка пересечения серединных перпендикуляров будет являться центром описанной окружности. Радиусом будет являться расстояние от этой точки до любой из вершин треугольника.
*** см. Билет 46.
Билет 31.
III
II
I




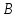
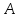
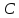
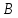

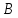
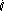


Подобные треугольники – треугольники, у которых углы соответственно равны, а стороны одного пропорциональны сходственным сторонам другого.
Первый признак подобия треугольников
Определение: Если два угла одного треугольника соответственно равны двум углам другого треугольника, то треугольники подобны.
Доказательство:
Допустим, даны Δ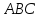 и Δ
и Δ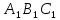 такие, что
такие, что
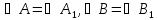 .
.
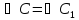 по теореме о сумме углов треугольника.
Теперь найдем площадь первого треугольника:
по теореме о сумме углов треугольника.
Теперь найдем площадь первого треугольника:
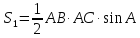 .
Площадь второго треугольника можно
найти по формуле
.
Площадь второго треугольника можно
найти по формуле
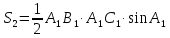 .
Но
.
Но
 ,
значит и
,
значит и
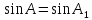 .
Тогда:
.
Тогда:
 .
Аналогично,
.
Аналогично,
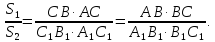 Отсюда,
Отсюда,
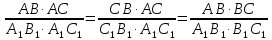 ,
значит, треугольники подобны.
,
значит, треугольники подобны.
