
- •Числові методи в інформатиці
- •Постановка задачі інтерполювання. Обчислення значень многочлена Лагранжа. Схема Ейткена.
- •Застосування
- •Побудова таблиці розділених різниць. Обчислення значень інтерполяційного полінома Ньютона. Інтерполяційний поліном Ньютона
- •Ітераційні методи уточнення коренів нелінійних рівнянь.
- •Метод поділу проміжку навпіл (половинного ділення).
- •Значення задається в межах 10 –410 –6.
- •Метод хорд (метод помилкового положення, метод пропорційних частин)
- •Метод січних Якщо знаходження f’(X) коштує дорогого, або неможливе, метод січних є кращим вибором, ніж метод Ньютона.
- •Абсциси точок а1а2; в1в2… – преставляють собою відповідно послідовне наближення кореня х*.
- •Методи розв’язування систем лінійних алгебраїчних рівнянь.
- •Множина розв'язків
- •Методи розв'язання
- •Метод послідовного виключення
- •Точні методи
- •Ітераційні методи
- •Постановка задачі числового інтегрування. Інтерполяційні формули.
- •Постановка задачі наближеного інтегрування функцій
Числові методи в інформатиці
-
Постановка задачі інтерполювання. Обчислення значень многочлена Лагранжа. Схема Ейткена.
Інтерполяція — в обчислювальній математиці спосіб знаходження проміжних значень величини за наявним дискретному наборі відомих значень.
Багатьом із тих, хто стикається з науковими та інженерними розрахунками часто доводиться оперувати наборами значень, отриманих експериментальним шляхом чи методомвипадкової вибірки. Як правило, на підставі цих наборів потрібно побудувати функцію, зі значеннями якої могли б з високою точністю збігатися інші отримувані значення. Така задача називається апроксимацією кривої. Інтерполяцією називають такий різновид апроксимації, при якій крива побудованої функції проходить точно через наявні точки даних.
Існує також близька до інтерполяції задача, що полягає в апроксимації якої-небудь складної функції іншою, простішою функцією. Якщо деяка функція занадто складна для продуктивних обчислень, можна спробувати обчислити її значення в декількох точках, а за ними побудувати, тобто інтерполювати, простішу функцію. Зрозуміло, використання спрощеної функції не дозволяє одержати такий ж точні результати, які давала б початкова функція. Але, для деяких класів задач, досягнутий виграш у простоті і швидкості обчислень може переважити отриманий огріх у результатах.
На
відрізку ![]() задано N точок
задано N точок ![]() що
називаються вузлами інтерполяції, і
значення деякої функції
що
називаються вузлами інтерполяції, і
значення деякої функції ![]() в
цих точках:
в
цих точках: ![]() Потрібно
побудувати функцію
Потрібно
побудувати функцію ![]() (
функцію, що інтерполює ), яка б збігалася
з
(
функцію, що інтерполює ), яка б збігалася
з ![]() у
вузлах інтерполяції і наближала її між
ними, тобто таку, що
у
вузлах інтерполяції і наближала її між
ними, тобто таку, що ![]() Геометрична
інтерпретація задачі інтерполяції
полягає в тому, що потрібно знайти таку
криву
Геометрична
інтерпретація задачі інтерполяції
полягає в тому, що потрібно знайти таку
криву![]() певного
типу, що проходить через задану систему
точок
певного
типу, що проходить через задану систему
точок ![]() За
допомогою цієї кривої можна знайти
наближене значення
За
допомогою цієї кривої можна знайти
наближене значення ![]() де
де ![]() Задача
інтерполяції стає однозначною, якщо
замість довільної функції
Задача
інтерполяції стає однозначною, якщо
замість довільної функції ![]() шукати
многочлен
шукати
многочлен ![]() степеня
не вище N, що задовольняє умови
степеня
не вище N, що задовольняє умови
![]()
Інтерполяційний
многочлен ![]() завжди
однозначний, оскільки існує тільки один
многочлен степеня N - 1, що в даних точках
набуває заданих значень. Існує декілька
способів побудови інтерполяційного
многочлена.
завжди
однозначний, оскільки існує тільки один
многочлен степеня N - 1, що в даних точках
набуває заданих значень. Існує декілька
способів побудови інтерполяційного
многочлена.
Визначення
Нехай маємо n значень xі, кожному з який відповідає своє значення yі. Потрібно знайти таку функцію F, що:
![]()
При цьому:
хі називають вузлами інтерполяції
пари (xі, yі) називають точками даних чи базовими точками
різницю між «сусідніми» значеннями xі-xі-1 — кроком
функцію F (x) — функцією, що інтерполює чи інтерполянтом.
Інтерполяцій́ний
многочле́н Лагра́нжа — многочлен мінімального степеня,
що приймає дані значення у даному наборі
точок. Для n +
1 пар
чисел ![]() ,
де всі
,
де всі ![]() різні,
існує єдиний многочлен
різні,
існує єдиний многочлен ![]() степеня
не більшого від n,
для якого
степеня
не більшого від n,
для якого ![]() .
.
У найпростішому випадку n = 1 - це лінійний многочлен, графік якого — пряма, що проходить через дві задані точки.
Лагранж запропонував спосіб обчислення таких многочленів:
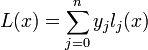
де базисні поліноми визначаються за формулою:

Очевидно, що lj(x) мають такі властивості:
-
Це поліноми степеня n
-

-
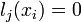 при
при 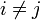
Звідси випливає, що L(x), як лінійна комбінація lj(x), може мати степінь не більший від n, та L(xj) = yj.
