Застосування

Поліноми Лагранжа використовуються для інтерполяції, а також для чисельного інтегрування.

Нехай для функції f(x) відомі значення y_j = f(x_j) у деяких точках. Тоді ця функція може інтерполюватися як

Зокрема,

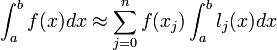
Значення інтегралів від l_j не залежать від f(x), тож їх можна обчислювати заздалегідь, знаючи послідовність x_i.

Схема Эйткена предлагает более удобную форму вычисления по формуле Лагранжа. Основная идея данного метода заключается в следующем. На первом этапе вычисляются многочлены ,построенные на каждой паре соседних узлов:

,

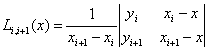Затем на их основе вычисляются многочлены, построенные на тройках соседних узлов:

,

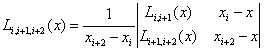и т.д., пока не получится один многочлен, построенный на всех узлах интерполяции:

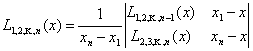
Нетрудно убедиться, что  .

2. Побудова таблиці розділених різниць. Обчислення значень інтерполяційного полінома Ньютона. Інтерполяційний поліном Ньютона

Інтерполяційна формула Лагранжа має два суттєвих недоліки:

1. формула громіздка- кожен доданок є многочленом n-го степеня;

2. якщо з якоїсь причини додаються вузли інтерполювання (наприклад, якщо отримана інтерполяційна формула неточна), то всі обчислення необхідно повторювати знову – ні один із доданків формули Лагранжа не зберігається.

Розглянем форму запису інтерполяційного полінома Р_n(х), яка допускає уточнення результатів інтерполяції послідовним додаванням нових вузлів. При цьому будем використовувати таке поняття як розділені різниці функцій.

Нехай маємо функцію f(x) і не обов"язково рівновіддалені вузли інтерполяції х_і (і=0, 1, 2, … , n).

Розділеними різницями 1-го порядку називають величини, які мають зміст, наприклад, середніх швидкостей зміни функції:

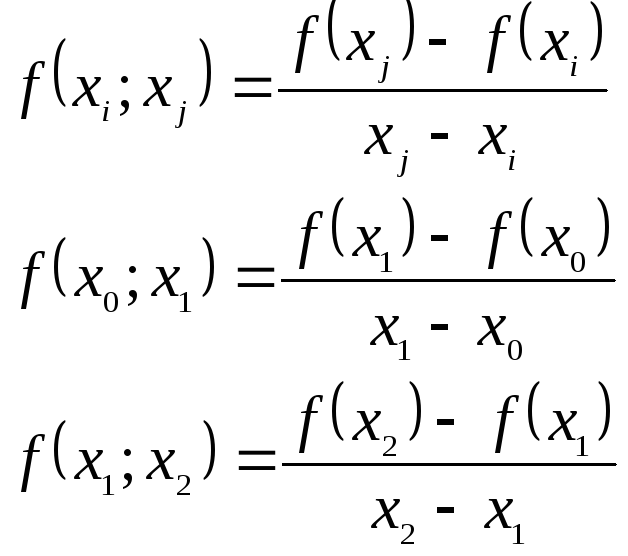(5)

Розділені різниці другого порядку визначаються співвідношеннями

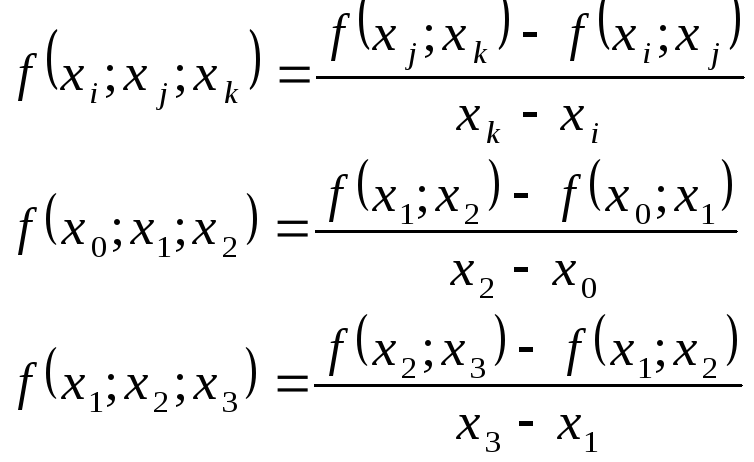(6)

Аналогічно, розділена різниця k−го порядку визначається через розділені різниці (k−1) порядку за рекурентною формулою:

(7)

Тепер перейдемо безпосередньо до самого інтерполяційного полінома Ньютона.

Маєм, наприклад, один вузол інтерполяції х₀.

Виходячи із визначення розділеної різниці 1−го порядку f(x; x₀) маємо:

Для розділених різниць другого порядку (два вузли − х₀, х₁)

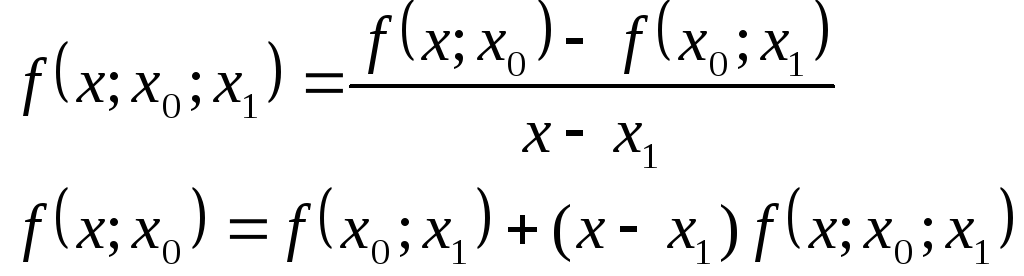
Підставляючи це значення у формулу для f(x)

Повторюючи цей процес, отримаємо (для n+1 вузлів інтерполяції):

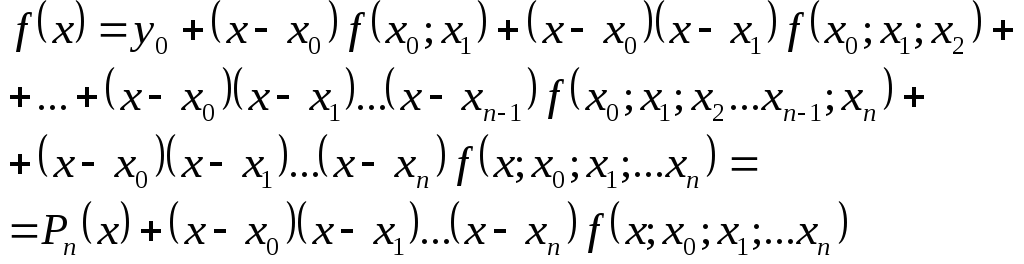(8)

Оскільки Р_n(x) − інтерполяційний поліном для функції f(x), то його значення у вузлах інтерполяції співпадають із значеннями функції f(x) (а, значить, і співпадають і розділені різниці)

Р_n(x_і) = f(x_і) = у_і, (і=),

оскільки залишковий член в цих вузлах

(х приймає значення х₀, х₁, … , х_n, тому один із співмножників завжди рівний 0, через те залишковий член у вузлах інтерполяції дорівнює нулю).

Тому замість (8) можна записати

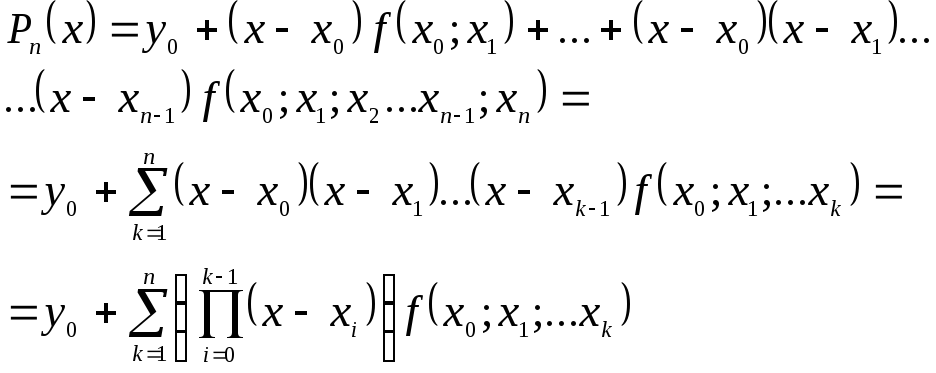(9)

Це і є інтерполяційний поліном Ньютона з розділеними різницями.

Для того, щоб пересвідчитись, що інтерполяційний поліном приймає значення у_і в вузлах інтерполяції х_і, візьмемо два вузли х₀ та х₁

n = 2 f(x) = y₀ + (x − x₀)f( x₀ ; x₁) + (x − x₀)(x − x₁)f(x; x₀; x₁)

При x = x₁

f(x₁) = y₀ + (x₁ − x₀)(f(x₁) − f(x₀))/(x₁ − x₀) = у₀ + f(x₁) – f(x₀);

f(x₁) = f(x₁)

Якщо маєм чотири вузли інтерполяції (n=3), то поліном Ньютона має вигляд:

P_n(x) = y₀ + (x − x₀)f(x₀; x₁) + (x − x₀)(x−x₁)f(x₀; x₁; x₂) +

+ (x − x₀)(x − x₁)(x − x₂)f(x₀; x₁; x₂; x₃)

Якщо ж маєм вже шість вузлів, тобто n=5, то йде просте нарощу-вання формули:

P_n(x) = y₀ + (x − x₀)f(x₀; x₁) + (x − x₀)(x − x₁)f(x₀; x₁; x₂) +

+ (x − x₀)(x − x₁)(x − x₂)f(x₀; x₁; x₂; x₃) +

+ (x − x₀)(x − x₁)(x − x₂)(х − х₃)f(x₀; x₁; x₂; x₃; x₄) +

+ (x − x₀)(x − x₁)(x − x₂)(х − х₃)(х − х₄)f(x₀; x₁; x₂; x₃; x₄; x₅).

Приклад.

Знайти інтерполяційний поліном Ньютона:

х −3 −1 1 2

у 8 6 4 18 При n = 3 інтерполяційний поліном Ньютона буде мати вигляд:

P_n(x) = y₀ + (x − x₀)f(x₀; x₁) + (x − x₀)(x − x₁)f(x₀; x₁; x₂) +

+ (x − x₀)(x − x₁)(x − x₂)f(x₀; x₁; x₂; x₃)

j	xj	yj	k=1	k=2	k=3
0	х0 = −3	y0 = 8		0
1	x1 = −1	y1 = 6
2	x2 = 1	y2 = 4
3	x3 = 2	y3 = 18

Р₃(х) = 8 + (х + 3)(−1) + (х + 3)(х + 1)*0 + (х + 3)(х + 1)(х − 1)*1=

= 8 − х − 3 + (х + 3)(х² − 1) = 5 − х + х³ + 3х² − х − 3 =

= х³ + 3х² − 2х + 2

Перш ніж приступати до заповнення таблиці, розпишемо розділені різниці

Розділені різниці 1−го порядку

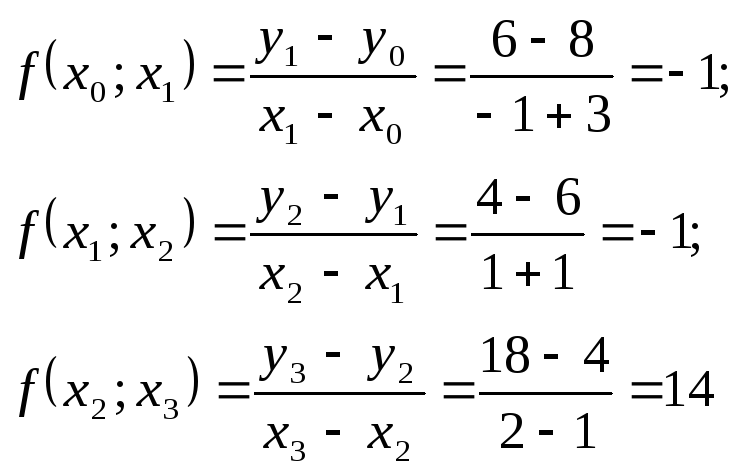
Розділені різниці 2−го порядку

Розділені різниці 3−го порядку

При написанні програми будемо користуватися наступним алгоритмом: позначимо через k – порядок розділених різниць (– межі зміни k, де n – порядок (найвищий) інтерполюючого полінома), а через і – число розділених різниць (– межі зміни і) для даного порядку k.

k=1 збереглося

k=2

k=3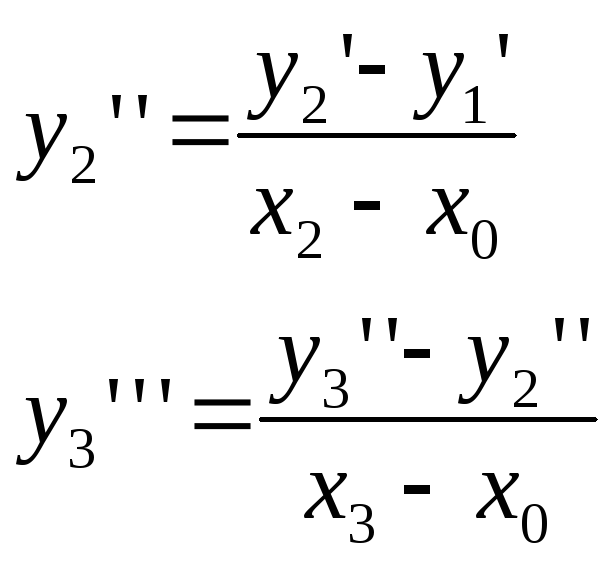

– кількість штрихів – це порядок

k = 1 до n

Для і = 0 до n ввести значення х_і, у_і

Для k = 1 до n

Для і = n до k з кроком –1

у_і = (у_і – у_і–1)/( х_і – х_і–1)

Тоді відповідно збережуться у₀, у₁΄, у₂΄΄, у₃΄΄΄

І нтерполяція функції у = |x – 5| з допомогою полінома Ньютона на 6-10 точках.