
- •Числові методи в інформатиці
- •Постановка задачі інтерполювання. Обчислення значень многочлена Лагранжа. Схема Ейткена.
- •Застосування
- •Побудова таблиці розділених різниць. Обчислення значень інтерполяційного полінома Ньютона. Інтерполяційний поліном Ньютона
- •Ітераційні методи уточнення коренів нелінійних рівнянь.
- •Метод поділу проміжку навпіл (половинного ділення).
- •Значення задається в межах 10 –410 –6.
- •Метод хорд (метод помилкового положення, метод пропорційних частин)
- •Метод січних Якщо знаходження f’(X) коштує дорогого, або неможливе, метод січних є кращим вибором, ніж метод Ньютона.
- •Абсциси точок а1а2; в1в2… – преставляють собою відповідно послідовне наближення кореня х*.
- •Методи розв’язування систем лінійних алгебраїчних рівнянь.
- •Множина розв'язків
- •Методи розв'язання
- •Метод послідовного виключення
- •Точні методи
- •Ітераційні методи
- •Постановка задачі числового інтегрування. Інтерполяційні формули.
- •Постановка задачі наближеного інтегрування функцій
Ітераційні методи
Ітераційні методи встановлюють процедуру уточнення певного початкового наближення до розв'язку. При виконанні умов збіжності вони дозволяють досягти будь-якої точності просто повторенням ітерацій. Перевага цих методів у тому, що часто вони дозволяють досягти розв'язку з наперед заданою точністю швидше, а також розв'язувати більші системи рівнянь. Суть цих методі полягає в тому, щоб знайти нерухому точку матричного рівняння:
![]() ,
,
еквівалентного
початковій системі лінійних алгебраїчних
рівнянь. При ітерації ![]() в
правій частині рівняння заміняється,
наприклад, у методі
Якобі на
наближення, знайдене на попередньому
кроці:
в
правій частині рівняння заміняється,
наприклад, у методі
Якобі на
наближення, знайдене на попередньому
кроці:
![]() .
.
Збіжність
ітераційної процедури досягається
вибором матриці ![]() ,
що залежить від задачі. Умови збіжності
конкретні для кожного конктретного
метода.
,
що залежить від задачі. Умови збіжності
конкретні для кожного конктретного
метода.
Серед ітераційних методів можна відзначити найпопулярніші:
-
Метод Якобі
-
Метод Зейделя
-
Постановка задачі числового інтегрування. Інтерполяційні формули.
Інтерполяційні формули, формули, що дають наближене вираження функції в = f ( x ) за допомогою інтерполяції, тобто через інтерполяційний многочлен Р n ( х ) міри n , значення якого в заданих точках x 0 , x 1 ..., х n збігаються з значеннями в 0 , в1 ..., у n функції f в цих крапках. Многочлен Р n ( х ) визначається єдиним чином, але залежно від завдання його зручно записувати різними по вигляду формулами.
Постановка задачі наближеного інтегрування функцій
Важливе значення на практиці мають числові методи обчислення інтегралів функцій
 .
.
Задача числового інтегрування функцій полягає в обчисленні значення визначеного інтеграла на підставі ряду значень підінтегральної функції.
Формули для обчислення однократного інтеграла називаються квадратурними, а подвійного інтеграла – кубатурними.
Для
визначеного інтеграла  ,
де
,
де ![]() –
неперервна на відрізку
–
неперервна на відрізку ![]() ,
наближена рівність
,
наближена рівність
 , (51)
, (51)
де –
деякі числа, –
точки відрізку ![]() ,
називається квадратурною
формулою,
що визначається вагами та
вузлами
,
називається квадратурною
формулою,
що визначається вагами та
вузлами ![]() .
.
Кажуть,
що квадратурна
формула є точною для багаточленів
степеня , якщо при
заміні ![]() на
довільний алгебраїчний багаточлен
степеня
на
довільний алгебраїчний багаточлен
степеня ![]() наближена
рівність (51) стає точною.
наближена
рівність (51) стає точною.
Звичайний
шлях у числовому інтегруванні полягає
в тому, що задану функцію ![]() на
відрізку
на
відрізку ![]() замінюють
інтерполяційною або апроксимуючою
функцією
замінюють
інтерполяційною або апроксимуючою
функцією ![]() простого
вигляду (наприклад, поліномом), а потім
наближено припускають:
простого
вигляду (наприклад, поліномом), а потім
наближено припускають:
 .
.
Функція ![]() має
бути такою, щоб інтеграл
має
бути такою, щоб інтеграл 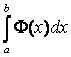 обчислювався
безпосередньо.
обчислювався
безпосередньо.
Теорема (узагальнена теорема про середнє).
Нехай ![]() ,
причому
,
причому ![]() ,
, ![]() .
Тоді існує така точка
.
Тоді існує така точка ![]() ,
що
,
що  .
.
Доведення. Позначимо ![]() ,
, ![]() .
.
Тоді,
оскільки ![]() , справедлива
подвійна нерівність:
, справедлива
подвійна нерівність: ![]() ,
, ![]() ,
,
і,
отже, ![]() .
.
Звідси,
оскільки  ,
, ![]() , слідує
існування такого числа с,
що задовольняє подвійній нерівності:
, слідує
існування такого числа с,
що задовольняє подвійній нерівності: ![]() ,
для якого справедливо:
,
для якого справедливо:

Оскільки ![]() –
неперервна функція, то знайдеться така
точка
–
неперервна функція, то знайдеться така
точка ![]() ,
в якій
,
в якій ![]() ,
що задовольняє умові теореми.
,
що задовольняє умові теореми.
Теорему доведено.
Нехай
для функції ![]() відомі
значення
відомі
значення ![]() ,
, ![]() у
(
у
(![]() )-й
точках
)-й
точках ![]() відрізка
відрізка ![]() .
.
Потрібно
наближено знайти  .
.
За даними
значеннями функції у вузлах ![]() можна
побудувати інтерполяційний багаточлен,
наприклад, Лагранжа:
можна
побудувати інтерполяційний багаточлен,
наприклад, Лагранжа:
 ,
,
причому ![]() .
.
Замінюючи
функцію ![]() багаточленом
багаточленом ![]() ,
отримаємо рівність:
,
отримаємо рівність:
 , (52)
, (52)
де ![]() –
похибка квадратурної формули (52) або
остаточний член.
–
похибка квадратурної формули (52) або
остаточний член.
Звідси, скориставшись виразом для багаточлена Лагранжа, отримаємо наближену квадратурну формулу:
 , (53)
, (53)
де  ,
, ![]() .
.
Якщо
границі інтегрування ![]() та
та ![]() є
вузлами інтерполяції, то квадратурна
формула (53) називається квадратурною
формулою „замкненого
типу”,
в іншому випадку – „відкритого
типу”.
є
вузлами інтерполяції, то квадратурна
формула (53) називається квадратурною
формулою „замкненого
типу”,
в іншому випадку – „відкритого
типу”.
Для
обчислення коефіцієнтів ![]() зазначимо,
що:
зазначимо,
що:
1)
коефіцієнти ![]() при
даному розташуванні вузлів не залежать
від вибору функції
при
даному розташуванні вузлів не залежать
від вибору функції ![]() ;
;
2) для
функції ![]() ,
що є багаточленом
степеня
,
що є багаточленом
степеня ![]() від
від ![]() ,
формула (53) є точною, оскільки
,
формула (53) є точною, оскільки ![]() .
.
Покладаючи ![]() у
формулі (53), отримаємо лінійну систему
з
у
формулі (53), отримаємо лінійну систему
з ![]() -го
рівняння:
-го
рівняння:

де  ,
,
з якої
можна обчислити коефіцієнти ![]() .
.
Зазначимо, що при використанні цього методу не треба фактично будувати багаточлен Лагранжа.
