3. Ітераційні методи уточнення коренів нелінійних рівнянь.

Ітераційні (або наближені) методи – це методи послідовних наближень. В них необхідно задати деякий наближений розв’язок – так зване початкове наближення. Після цього з допомогою деякого алгоритму проводиться один цикл обчислень, котрий називається ітерацією. В результаті ітерації знаходять нове наближення. Ітерації проводять до тих пір, доки не одержать розв’язок із заданою похибкою. Об’єм обчислень при цьому наперед не відомий.

При використанні ітераційних методів виникає проблема збіжності чисельного методу. Вона (збіжність) означає близькість одержаного після проведення ітерації розв’язку до істинного розв’язку. Збіжність ітераційного процесу: якщо в результаті проведення ітерацій одержуємо деяку послідовність х₁, х₂, … , х_n (не важливо, це скалярні чи векторні величини), та якщо ця послідовність збігається до точного розв’язку х = а, тобто існує границя цієї послідовності , то метод є збіжним.

Метод поділу проміжку навпіл (половинного ділення).

Алгоритм методу половинного ділення.

1. Ввести, задати значення параметрів а, b та граничної абсолютної похибки  .

2. Обчислити значення функції f (x) в точці а, тобто обчислити f (а).

3. Поділити проміжок [а, b] навпіл, тобто знайти точку x_s

x_s = (a + b)/2.

4. Перевірити умову f (x_s) = 0? Якщо так, то перейти до п.7.

5. Якщо добуток f (а) f (x^*)>0?, то a: = x_s, в протилежному випадку b: = x_s.

6. Якщо |b - a| >  , то перейти до п.3.

7. Надрукувати (вивести) значення x_s.

8. Закінчити виконання програми.

Значення  задається в межах 10 –410 –6.

Обчислення F(a)

x_s = (a + b)/2

b = x_s

ні

так

ні

a= x^*_s

так

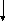
Метод, як правило використовується для грубого знаходження кореня рівняння. При підвищенні точності (тобто при зменшенні  ) значно зростає об’єм обчислювальної роботи.

Число ітерацій значне (при |b - a| >  ), тому збіжність його повільна.

Однак збіжність ця гарантована завжди (надійний метод). Крім того, простота реалізації методу зменшує число допоміжних операцій і частково компенсує затрати машинного часу через повільну збіжність.

Метод хорд (метод помилкового положення, метод пропорційних частин)

Цей метод забезпечує швидку збіжність, ніж метод половинного ділення. Ідея методу полягає в тому, що на достатньо малому проміжку [a,b] функція f(x) змінюється лінійно і тому дуга кривої f(x) замінюється хордою, яка її стягує. За наближене значення кореня можна прийняти точку перетину хорди з віссю абсцисс

Ітераційна формула

Метод хорд має лінійну збіжність – похибка на наступній ітерації пропорційна (лінійно) похибці на попередній ітерації.

Метод січних Якщо знаходження f’(X) коштує дорогого, або неможливе, метод січних є кращим вибором, ніж метод Ньютона.

В цьому алгоритмі починають з двома початковими числами х_n та х_n–1. Абсциси n, n-1 вибирають по одну сторону від кореня. На наступне уточнення х_n+1 одержують з х_n та х_n–1 як єдиний нуль лінійної функції, що приймає значення f(х_n) в х_n та f(х_n–1) в х_n–1. Ця лінійна функція являє собою січну до кривої f(x), що проходить через її точки з абсцисами х_n та х_n–1 – звідси назва методу січних.

Метод простої ітерації

Для застосування цього методу рівняння f(x) = 0 представляється у вигляді

(1)

Виберемо за початкове наближення кореня значення і підставимо в праву частину рівняння (1). Одержимо деяке число

(2)

Підставляючи в праву частину рівності (2) замість х₀ значення х₁ одержимо нове число

Повторний процес буде мати наступну послідовність

.

Якщо ця послідовнясть збіжна, то границя цієї послідовності – корінь рівняння f(x) = 0 і може бути обчислений з будь-якою точністю.

Геометрично метод ітерації можна пояснити наступним чином. Побудуємо на площині хоу графіки функцій у = х і . Відштовхуючись від деякої точки будуємо ламану лінію А₀В₁А₁В₂… («сходинки») , вершини яких обов’язково паралельні осі х і у , вершини А₀А₁А₂ лежать на кривій , а вершини В₁В₂…– на прямій у = х.