
- •Новочеркасск 2008 Содержание
- •Тема №1 Модели и моделирование.
- •Погрешности численных методов.
- •Тема №2 Аппроксимация функций.
- •Интерполяционная формула Лагранжа.
- •Сплайны
- •Сплайны третьей степени
- •Метод наименьших квадратов
- •Тема №3 Решение нелинейных уравнений.
- •Метод половинного деления.
- •Метод простых итераций.
- •Метод Хорд
- •Метод Ньютона (касательных).
- •Тема №4 Решение систем линейных уравнений.
- •1) Прямые
- •2) Итерационные
- •Метод Гаусса.
- •Метод прогонки.
- •Уточнение решения (итерационный метод).
- •Метод Гаусса-Зейделя.
- •Тема №5 Решение систем не линейных уравнений.
- •Простой Итерации
- •Метод Ньютона для систем уравнений.
- •Метод возмущения параметров.
- •Тема №6 Численное интегрирование.
- •Метод прямоугольников.
- •Метод трапеции
- •Метод Симпсона.
- •Метод Гаусса.
- •Метод Монте-Карло.
- •Метод Монте-Карло для вычисления кратных интегралов.
- •Тема №7 Решение обыкновенных дифференциальных уравнений (оду).
- •Метод Эйлера.
- •Модифицированный метод Эйлера.
- •Метод Рунге – Кутта.
- •Метод Рунге-Кутта для решения систем оду
- •Метод Рунге-Кутта для оду высших порядков.
- •Метод стрельбы.
- •Метод конечных разностей (мкр) (метод сеток).
- •Тема №8 Решение дифференциальных уравнений с частными производными.
- •Уравнение теплопроводности.
- •Явная разностная схема для уравнения теплопроводности.
- •Неявная разностная схема для уравнения теплопроводности.
- •Тема №9 Задачи оптимизации.
- •Метод половинного деления.
- •Метод золотого сечения.
- •Метод покоординатного подъёма (спуска).
- •Метод градиентного подъёма (спуска).
- •Метод наискорейшего подъёма.
- •Тема №10 Задания для самостоятельной проработки. Транспортная задача.
- •Задача о ресурсах.
- •Волновое уравнение.
- •Уравнение Лапласа.
Волновое уравнение.
Одним из наиболее распространенных в инженерной практике уравнений с частными производными второго порядка является волновое уравнение, описывающее различные виды колебаний. Поскольку колебания — процесс нестационарный, то одной из независимых переменных является время t. Кроме того, независимыми переменными в уравнении являются также пространственные координаты х, у, z. В зависимости от их количества различают одномерное, двумерное и трехмерное волновые уравнения.
Одномерное волновое уравнение описывает продольные колебания стержня, сечения которого совершают плоскопараллельные колебательные движения, а также поперечные колебания тонкого стержня и другие задачи. Двумерное волновое уравнение используется для исследования колебаний тонкой пластины. Трехмерное волновое уравнение описывает распространение волн в пространстве.
Рассмотрим одномерное волновое уравнение, которое можно записать в виде
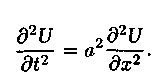
Для поперечных колебаний струны искомая
функция U(x,t)
описывает положение струны в момент
t. В этом случае
![]() ,
где Т — натяжение
струны,
,
где Т — натяжение
струны,
![]() — ее линейная
плотность. Уравнение записано для
случая свободных колебаний. Сопротивление
среды колебательному процессу не
учитывается.
— ее линейная
плотность. Уравнение записано для
случая свободных колебаний. Сопротивление
среды колебательному процессу не
учитывается.
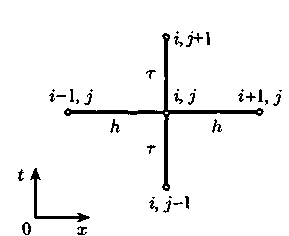
Решим задачу Коши для этого уравнения. Вот условия задачи:
![]()
Эти условия описывают
начальную форму струны
![]() и скорость
ее точек.
и скорость
ее точек.
На практике чаще
приходится решать не задачу Коши для
бесконечной струны, а смешанную
задачу для ограниченной струны некоторой
длины
![]() .
В этом случае задают граничные условия
на ее концах. В частности, при закрепленных
концах их смещения равны нулю, и граничные
условия имеют вид
.
В этом случае задают граничные условия
на ее концах. В частности, при закрепленных
концах их смещения равны нулю, и граничные
условия имеют вид
![]()
Для решения такой задачи используем
явную трехслойную схему типа крест.
Заменим в начальном уравнении вторые
производные искомой функции U
по t и х их
конечно-разностными соотношениями с
помощью значений сеточной функции
![]() в узлах сетки
в узлах сетки
![]()
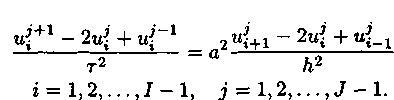
Отсюда можно найти явное выражение для значения сеточной функции на (j + 1)-м слое:
![]()
Здесь, как обычно в трехслойных схемах, для определения неизвестных значений на (j + 1)-м слое нужно знать решения на j-м и (j — 1)-м слоях. Поэтому начать счет можно лишь для второго слоя, а решения на нулевом и первом слоях должны быть известны. Они находятся с помощью начальных условий. На нулевом слое имеем
![]()
Для получения решения на первом слое
воспользуемся вторым начальным
условием. Производную
![]() заменим конечно-разностной
аппроксимацией.
заменим конечно-разностной
аппроксимацией.
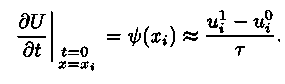
Из этого соотношения можно найти значения сеточной функции на первом временном слое:
![]()
Отметим, что аппроксимация начального
условия в таком виде ухудшает
аппроксимацию исходной дифференциальной
задачи: погрешность
аппроксимации становится порядка
![]() ,т.
е. первого порядка по
,т.
е. первого порядка по
![]() ,
хотя сама схема
имеет второй порядок аппроксимации по
h
и
,
хотя сама схема
имеет второй порядок аппроксимации по
h
и
![]() .
Положение можно исправить, если взять
более точное представление
.
Положение можно исправить, если взять
более точное представление
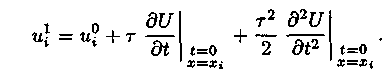
Так как,
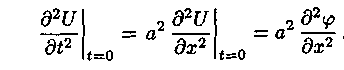
то:
![]()
Теперь разностная схема
обладает погрешностью аппроксимации
порядка
![]() .
.
Рассмотренная разностная схема решения задачи условно устойчива. Необходимое и достаточное условие устойчивости имеет вид
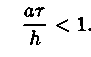
Следовательно, при выполнении этого
условия и с учетом аппроксимации
схема
сходится
к исходной задаче со
скоростью
![]() .
.
