
- •Глава 2. Введение в анализ
- •§ 1. Некоторые свойства множества действительных чисел
- •§ 2. Предел последовательности
- •§ 3. Предел функции
- •§ 4. Бесконечно малые и их свойства
- •§ 5. Основные теоремы о пределах
- •§ 6. Замечательные пределы
- •§ 7. Непрерывность функции. Классификация точек разрыва
- •§ 8. Свойства непрерывных функций
- •§ 9. Сравнение функций. Асимптотические равенства
§ 3. Предел функции
Пусть функция
![]() определена в окрестности точки
определена в окрестности точки
![]() =
=
![]() за исключением, быть может, самой точки
за исключением, быть может, самой точки
![]() .
Точка
.
Точка
![]() может быть и бесконечно удалённой.
может быть и бесконечно удалённой.
Определение 1
(Гейне). Число
![]() называется пределом функции
называется пределом функции
![]() в точке
в точке
![]() =
=
![]() ,
если для любой сходящейся к
,
если для любой сходящейся к
![]() последовательности аргумента
последовательности аргумента
![]() соответствующая последовательность
значений функции
соответствующая последовательность
значений функции
![]() сходится к
сходится к
![]() .
.
Пишут
![]()
![]() =
=
![]() ,
или
,
или
![]()
![]() при
при
![]() .
.
Если предел функции существует, то он единственный. Это следует из единственности предела последовательности.
Пример 1.
Найти
![]() .
.
Решение. Пусть предел существует. Выберем две последовательности аргумента, сходящиеся к нулю:
![]() =
=
![]() и
и
![]() =
=
 .
Соответствующие последовательности
значений функции следующие:
.
Соответствующие последовательности
значений функции следующие:
![]() =
=
![]() =
=
=
![]() =
0,
=
0,
![]() =
=
![]() =
=
![]() = 1,
= 1,
т.е. обе
последовательности являются постоянными.
Поскольку пределом постоянной является
сама постоянная (см. §2),
то в точке
![]() =
0
мы получим два предела функции 0 и 1, чего
не может быть. Следовательно наше
предположение о существовании предела
в точке
=
0
мы получим два предела функции 0 и 1, чего
не может быть. Следовательно наше
предположение о существовании предела
в точке
![]() =
0
не верно. Данная функция не имеет предела
в нуле.
=
0
не верно. Данная функция не имеет предела
в нуле.
Определение 2
(Коши). Число
![]() называется пределом функции
называется пределом функции
![]() в точке
в точке
![]() =
=
![]() ,
если для любого
,
если для любого
![]() >
0
существует число
>
0
существует число
![]() > 0 такое,
что для всех
> 0 такое,
что для всех
![]()
O(
O(![]() ,
,![]() )
имеет место неравенство
)
имеет место неравенство
![]() <
<
![]() .
(
.
(![]() > 0
O (
> 0
O (![]() ,
,![]() )
)
![]()
O(
O(![]() ,
,![]() )
)
![]()
O (
O (![]() ,
,![]() )).
)).
Пример 2.
Доказать, что
![]() = 1.
= 1.
Решение.
По определению Коши
![]() <
<
![]() ,
если
,
если
![]() =
=
![]() <
<
![]() .
Если найдем
.
Если найдем
![]() для любого
для любого
![]() > 0 такое,
что из второго неравенства будет
следовать первое, то задача будет решена.
> 0 такое,
что из второго неравенства будет
следовать первое, то задача будет решена.
![]() = 1 –
= 1 –
![]() =
=
![]()
2
2
![]() <
<
![]()
![]() <
<
![]() .
.
Положим
![]() =
=
![]() ,
тогда для всех
,
тогда для всех
![]() <
<
![]() выполняется неравенство
выполняется неравенство
![]() <
<
![]() и задача решена.
и задача решена.
Упражнение.
Доказать, что
![]() = 0.
= 0.
Замечание. Выше приведено два определения предела функции, однако определение должно быть единственным. Поэтому, если за определение взять формулировку Гейне, то формулировка Коши будет теоремой, и её можно доказать. И наоборот.

![]() называется бесконечно большой в точке
называется бесконечно большой в точке
![]() =
=
![]() ,
если существует такая
,
если существует такая
![]() -окрестность
этой точки, что для
-окрестность
этой точки, что для
![]()
O (
O (![]() ,
,![]() )
)
![]() > M , где М >
0
– любое действительное число. Точка
> M , где М >
0
– любое действительное число. Точка
![]() может быть и бесконечно удалённой.
(
M > 0
может быть и бесконечно удалённой.
(
M > 0
![]() > 0 (
> 0 (![]()
O (
O (![]() ,
,![]() )
)
![]() > M).
> M).
Если
![]()
![]() ,
оставаясь меньше
,
оставаясь меньше
![]() ,
то предел
функции
,
то предел
функции
![]() в точке называется левым.
Пишут
в точке называется левым.
Пишут
![]() =
=
![]() .
Если
.
Если
![]()
![]() ,
оставаясь больше
,
оставаясь больше
![]() ,
то предел называют правым.
Пишут
,
то предел называют правым.
Пишут
![]() =
=
![]() .
Правый и левый пределы называют
односторонними
пределами.
Если
.
Правый и левый пределы называют
односторонними
пределами.
Если
![]()
![]() ,
то функция в точке
,
то функция в точке
![]() =
=
![]() предела не имеет, а имеет только
односторонние пределы. Если
предела не имеет, а имеет только
односторонние пределы. Если
![]() =
=
![]() ,
то функция имеет в точке
,
то функция имеет в точке
![]() предел. И наоборот, если функция имеет
предел в точке
предел. И наоборот, если функция имеет
предел в точке
![]() =
=
![]() ,
то она имеет равные между собой левый
и правый пределы.
,
то она имеет равные между собой левый
и правый пределы.
§ 4. Бесконечно малые и их свойства
Определение.
Функция
![]() называется бесконечно
малой в точке
называется бесконечно
малой в точке
![]() =
=
![]() ,
если её предел в этой точке равен нулю,
,
если её предел в этой точке равен нулю,
![]() =
0. С помощью
=
0. С помощью
![]() ,
,
![]() это можно записать так:
это можно записать так:
![]() > 0
> 0
![]() > 0 (
> 0 (![]()
O (
O (![]() ,
,![]() )
|
)
|![]() |
<
|
<
![]() ).
).
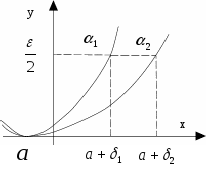
Доказательство.
Докажем теорему для двух слагаемых
![]() и
и
![]() .
По условию теоремы
.
По условию теоремы
![]() <
<
![]() ,
если
,
если
![]() <
<
![]() ,
,
![]() <
<
![]() ,
если
,
если
![]() <
<
![]() .
.
Пусть
![]() = min
(
= min
(![]() ,
,![]() ),
тогда
),
тогда
![]() <
<
![]() и
и
![]() <
<
![]() ,
если
,
если
![]() <
<
![]() .
Т.к. неравенствa одинакового смысла
можно cкладывать, то имеем
.
Т.к. неравенствa одинакового смысла
можно cкладывать, то имеем
![]() +
+
![]() <
<
![]()
![]() <
<
![]() ,
если
,
если
![]() <
<
![]() .
Последняя
запись означает, что
.
Последняя
запись означает, что
![]() =
0. Теорема
доказана.
=
0. Теорема
доказана.
Теорема 2.
Произведение бесконечно малой в точке
![]() =
=
![]() функции
функции
![]() на ограниченную в этой точке функцию
на ограниченную в этой точке функцию
![]() есть функция бесконечно малая.
есть функция бесконечно малая.
Доказательство.
Запись
![]() >
0,
M
>
0
(
>
0,
M
>
0
(![]()
O (
O (![]() ,
,![]() )
)
![]() <
M)
означает, что функция
<
M)
означает, что функция
![]() ограниченна в точке
ограниченна в точке
![]() =
=![]() .
Запись
.
Запись
![]() >
0
>
0
![]() >
0
(
>
0
(![]() O(
O(![]() ,
,![]() )
|
)
|![]() |<
|<![]() )
означает, что
)
означает, что
![]() –
бесконечно малая в точке
–
бесконечно малая в точке
![]() =
=
![]() .
В наименьшей из двух окрестностей точки
.
В наименьшей из двух окрестностей точки
![]() =
=
![]() будут выполняться оба неравенства
будут выполняться оба неравенства
![]() < M и |
< M и |![]() |
<
|
<
![]() .
Перемножая неравенства, получим |
.
Перемножая неравенства, получим |![]()
![]() |<
|<![]()
![]() O(
O(![]() ,
,![]() ),
),
![]() = min(
= min(![]() ,
,![]() ).
Последняя запись означает , что
произведение
).
Последняя запись означает , что
произведение
![]()
![]() есть бесконечно малая в точке
есть бесконечно малая в точке
![]() =
=
![]() .
Теорема доказана.
.
Теорема доказана.
Теорема 3.
Если
![]() —
бесконечно малая в точке
—
бесконечно малая в точке
![]() =
=
![]() и не обращается в нуль в некоторой
окрестности этой точки, то
и не обращается в нуль в некоторой
окрестности этой точки, то
![]() =
=
![]() –
бесконечно
большая функция в этой точке. (Без
доказательства).
–
бесконечно
большая функция в этой точке. (Без
доказательства).
