
Глава 2. Операционное исчисление
§1. Преобразование Лапласа, основные понятия
Пусть
функция
![]() для всякого комплексного
для всякого комплексного
![]() является кусочно непрерывной по
действительной переменной
является кусочно непрерывной по
действительной переменной
![]()
Определение
1. Сходящийся
несобственный
интеграл
![]() зависящий от параметра
p,
называется равномерно
сходящимся
в области E,
если
зависящий от параметра
p,
называется равномерно
сходящимся
в области E,
если
![]()
при
![]() (Сравнить
с определением равномерной сходимости
ряда, см. §4
гл. 5, ч.1).
(Сравнить
с определением равномерной сходимости
ряда, см. §4
гл. 5, ч.1).
Теорема
1 (признак Вейерштрасса).
Если
![]()
![]() а интеграл
а интеграл
![]() сходится, то интеграл
сходится, то интеграл
![]() сходится
равномерно в области
E
(без доказательства).
сходится
равномерно в области
E
(без доказательства).
Теорема
2. Если функция
аналитическая в области E,
а несобственный интеграл
![]() сходится равномерно в области E,
то функция I(p)
является аналитической в области E,
при этом
сходится равномерно в области E,
то функция I(p)
является аналитической в области E,
при этом
![]() (без доказательства).
(без доказательства).
Определение
2. Комплекснозначная
функция
![]() называется оригиналом,
если она обладает следующими свойствами:
называется оригиналом,
если она обладает следующими свойствами:
![]()
![]()
![]() кусочно-непрерывная
функция;
кусочно-непрерывная
функция;
3)
функция имеет ограниченный рост, т.е.
![]()
![]()
![]()
Очевидно,
если
![]() то
то
![]()
![]()
Нижняя
грань
![]() всех таких
всех таких
![]() при которых выполняется неравенство,
называется показателем
роста функции
при которых выполняется неравенство,
называется показателем
роста функции
![]()
Например,
функция Хевисайда
![]() является оригиналом. Функции
является оригиналом. Функции
![]()
![]() -
оригиналы, а функции
-
оригиналы, а функции
![]() не являются оригиналами.
не являются оригиналами.
Определение
3. Функция
![]() называется изображением функции
по Лапласу или преобразованием Лапласа.
Пишут
называется изображением функции
по Лапласу или преобразованием Лапласа.
Пишут
![]() или
или
![]() L
- оператор
Лапласа.
L
- оператор
Лапласа.
Теорема
3. Если
функция
является оригиналом, то интеграл![]() (1)
(1)
сходится
для всех
![]() где
где
![]() показатель
роста функции
,
и определяет аналитическую в полуплоскости
показатель
роста функции
,
и определяет аналитическую в полуплоскости
![]() функцию F(p).
функцию F(p).
Доказательство.
Поскольку
![]() оригинал,
то
оригинал,
то
![]() Оценим подынтегральную функцию интеграла
(1).
Оценим подынтегральную функцию интеграла
(1).
![]() (2)
(2)
где
![]() Зафиксируем некоторое
Зафиксируем некоторое
![]() тогда получим функцию
тогда получим функцию
![]() такую, что
такую, что
![]() причем
причем
![]() сходится. Действительно,
сходится. Действительно,
![]() если
если
![]() По признаку Вейерштрасса интеграл (1)
сходится равномерно. А так как
подынтегральная функция является
аналитической, то из теоремы 2 следует,
что функция
По признаку Вейерштрасса интеграл (1)
сходится равномерно. А так как
подынтегральная функция является
аналитической, то из теоремы 2 следует,
что функция
![]() аналитическая в правой полуплоскости
аналитическая в правой полуплоскости
![]() Теорема доказана.
Теорема доказана.
Следствие.
Если
![]() изображение некоторого оригинала, то
изображение некоторого оригинала, то
![]() при
при
![]() Действительно, из теоремы 3 следует
Действительно, из теоремы 3 следует
![]() при
при
![]()
Следствие доказано.
Теорема 4. Если функция является оригиналом, а его изображение, то в любой точке непрерывности оригинала имеет место формула обращения
![]() (3)
(3)
где
В точках разрыва правая часть (3) равна
полусумме пределов слева и справа, т.е.
![]() (без доказательства).
(без доказательства).
Формулу (3) называют обратным преобразованием Лапласа, а формулу (1) - прямым.
Найдем изображения некоторых оригиналов.
Пусть
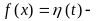 единичная функция Хевисайда. Согласно
(1), имеем
единичная функция Хевисайда. Согласно
(1), имеем
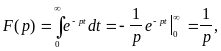 если
если
 Итак,
Итак,

Пусть
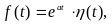
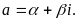 Согласно (1), имеем
Согласно (1), имеем
![]() если
если
![]()
![]() есть показатель роста данного оригинала.
Итак,
есть показатель роста данного оригинала.
Итак,
![]()
Замечание.
Поскольку
все оригиналы равны нулю при
![]() то их следует записывать так:
то их следует записывать так:
![]() Однако, ради сокращения записи множитель
Однако, ради сокращения записи множитель
![]() обычно опускают, но его всегда
подразумевают.
обычно опускают, но его всегда
подразумевают.
§2. Свойства преобразования Лапласа
1.
Линейность. Если
![]()
![]()
![]()
Действительно,
![]()
![]()
![]()
![]()
Пример
1. Найти
изображение оригинала
![]()
Решение.
![]()
![]()
Воспользовались
линейностью и результатом примера 2 §1.
Аналогично найдем
![]()
Смещение изображения. Если то
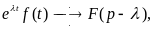 где
где
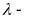 произвольное
комплексное число.
произвольное
комплексное число.
Действительно,
![]()
Пример
2. Найти
изображение оригинала
![]()
Решение.
Поскольку
![]() то
то
![]()
Аналогично
найдем
![]()
Запаздывание оригинала. Если то
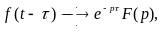 где
где
 Действительно,
Действительно,


![]()
![]()
![]()
Пример
3. Найти
изображение единичного импульса
длительности
![]() (см. рис. 1).
(см. рис. 1).
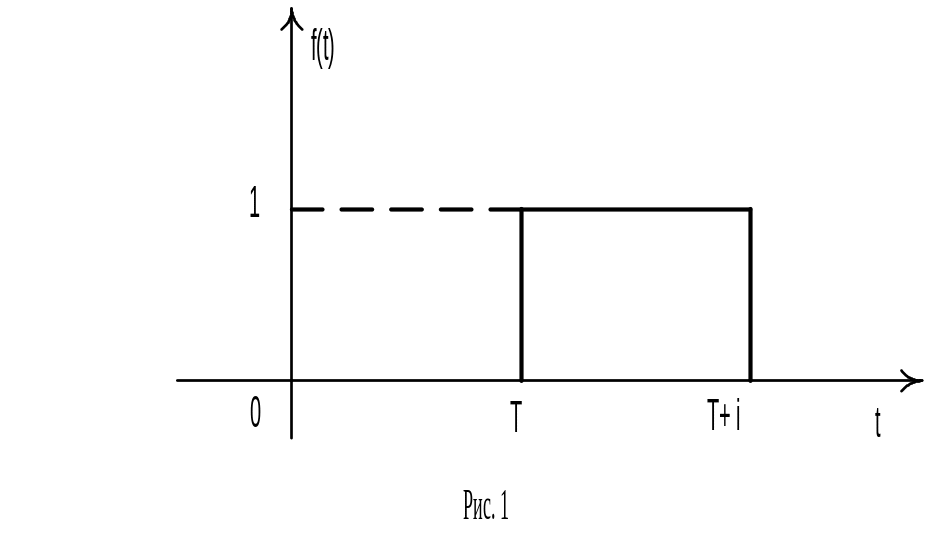
Решение.
![]() Тогда
Тогда
![]()
