2.3.Хвильові функції.

Хвильова функція гармонічного осцилятора, як випливає (2.3) має вигляд:

.

Нормуюча постійна визначається з умови:

(2.11)

Звідси отримаємо для : Отже нормована хвильова функція рівна:

(2.12)

Деякі властивості функцій .

(2.13)

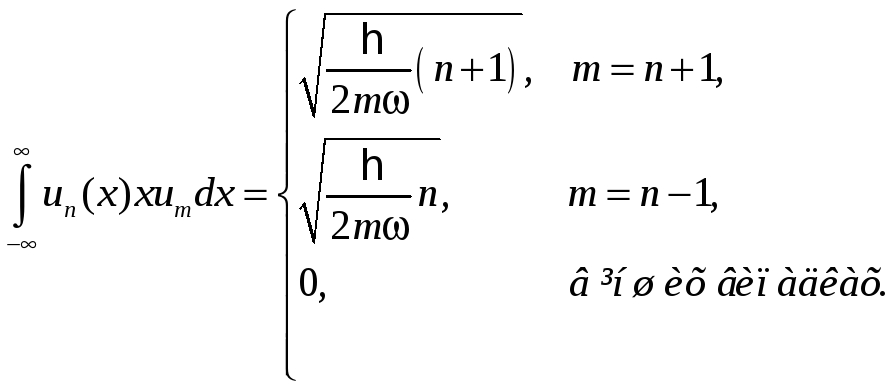(2.14)

2.3.Оператори породження і знищення.

Розглянемо оператори і , які визначаються наступним чином:

(2.15)

(2.16)

З співвідношень (2.13) і (2.14) випливає:

(2.17)

Рівняння (2.17) узгоджуються із операторними рівняннями:

(2.18)

Про оператори і здебільшого говорять, як про оператори народження і знищення. Такі назви пояснюються тим, що згідно (2.18) дія оператора (або ) на хвильову функцію , що відповідає стану з квантами енергії , переводять її в нову хвильову функцію стану з (або ) квантами, народжуючи (або знищуючи) один квант. Комутатор і рівний:

,

тут використовуємо, що . Отже,

. (2.19)

На основі (2.15) і (2.16) можна виразити і через і :

(2.20)

Підставивши (2.20) в гамільтоніан та використавши і маємо:

.

Оскільки , то:

. (2.21)

Це найбільш використовувана форма гамільтоніана гармонічного осцилятора, і саме вона буде зустрічатися в наступних лекціях. Оператор комутує з , і його власні значення рівні числу квантів . Це легко показати з допомогою рівняння (2.18).

Так, що в повному узгодженні з (2.21).

Лекція 3 Загальна теорія резонаторів

1. Розклад електромагнітного поля по модах резонатора.

Поле в резонаторі описується рівняннями Максвела :

(3.1)

Обмежимося випадком однорідного та ізотропного середовища без зарядів, тоді:

(3.2)

де e та m – відповідно діелектрична та електромагнітна проникливість середовища.

Розглянемо електричне поле і магнітне поле в об’ємі , який обмежений ідеально провідною поверхнею На ній повинні обертатися в нуль: дотична компонента вектора , тобто а також нормальна компонента тобто ( – одиничний вектор нормалі до поверхні ). Розкладемо і у ряди по системах ортогональних векторних полів і . Ця система полів, вперше використана Слеттером, задовольняє рівнянням

, (3.3)

(3.4)

де – будемо рахувати постійною величиною. Дотична складова вектора вздовж рівна нулю :

на . (3.5)

Візьмемо ротор від обох частин (3.3) і (3.4) і скористаємося векторною тотожністю:

Це приводить до відомих хвильових рівнянь:

(3.6)

З рівнянь (3.3), (3.4) і умови (3.5) випливає, що нормальна складова , рівна нулю на . Щоб це доказати, розглянемо на поверхні довільний замкнутий контур , що охоплює елемент поверхні , і інтеграл

(3.7)

де поле представлено у вигляді суми дотичної – і нормальної до поверхні компонентів. Перший член в правій частині (3.7) рівний нулю внаслідок (3.5), другий доданок рівний нулю через ортогональність векторів і Перетворимо ліву частину (3.7), скориставшись теоремою Стокса

Оскільки контур вибрано довільно, то

на . (3.8)

Докажемо, що функції і ортогональні в розумінні

; , (3.9)

Доведемо ортогональність функцій . Для доведення ортогональності аналогічне. Для доведення ортогональності скористаємося тотожністю:

Покладемо спочатку потім Віднімемо другу рівність від першої:

З рівняння (3.4) маємо Підставимо це в останню рівність:

.

Візьмемо інтеграл по об’єму від правої та лівої частини, для лівої частини скористаємося теоремою Гауса-Остроградського.

Врахувавши граничні умови (5.5) і векторну тотожність маємо:

Так як то ліва частина рівна нулю. Отже , коли

Виберемо функції і такими , щоб вони задовольняли умовам нормування:

(3. 10)

Ці умови будуть використовуватися на протязі багатьох лекцій. Поля і в резонаторі розкладемо в ряди:

(3.11)

де Підставши (3.11) в перше рівняння Максвела (3.1) з врахуванням (3.3) і (3.4) отримаємо :

(3.12)

(3.13)

Візьмемо похідну по часу правої і лівої частини рівняння (4.13) ще один раз і підставимо в це рівняння, отримаємо:

(3.14)

Звідси випливає, що – кругова ячастота коливань –ї моди.