
8.3. Смо с ожиданием
Рассмотрим аналитические модели СМО с ожиданием (наиболее распространенные СМО, в которых требования, поступившие в момент, когда все обслуживающие единицы заняты, становятся в очередь и обслуживаются по мере освобождения обслуживающих единиц).
Задачи с очередями являются типичными в производственных условиях, например при организации наладочных и ремонтных работ, при многостаночном обслуживании и т.д.
Постановка задачи в общем виде выглядит следующим образом.
Система
состоит из n
обслуживающих
каналов. Каждый из них может одновременно
обслуживать только одно требование. В
систему поступает простейший
(пуассоновский) поток требований с
параметром
 .
Если в момент поступления очередного
требования в системе на обслуживании
уже находится не меньше n
требований
(т.е. все каналы заняты), то это требование
становится в очередь и ждет начала
обслуживания. Время обслуживания каждого
требования tоб
является случайной величиной, которая
подчиняется экспоненциальному закону
распределения с параметром
.
Если в момент поступления очередного
требования в системе на обслуживании
уже находится не меньше n
требований
(т.е. все каналы заняты), то это требование
становится в очередь и ждет начала
обслуживания. Время обслуживания каждого
требования tоб
является случайной величиной, которая
подчиняется экспоненциальному закону
распределения с параметром
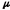 .
.
Как отмечалось выше, СМО с ожиданием можно разбить на две большие группы: замкнутые и разомкнутые. Особенности функционирования каждой из этих двух видов систем накладывают свой оттенок на используемый математический аппарат. Расчет характеристик работы СМО различного вида может быть проведен на основе расчета вероятностей состояний СМО (формулы Эрланга).
8.3.1. Замкнутая смо с ожиданием
Поскольку система замкнутая, то к постановке задачи следует добавить условие: поток поступающих требований ограничен, т.е. в системе обслуживания одновременно не может находиться больше m требований (m – число обслуживаемых объектов).
Такую систему можно классифицировать как многоканальную СМО (n – каналов) и ограниченной данной очереди l, причем n + l = m.
Граф состояний такой системы изображен на рис. 8.2.
…
…









…
Рис. 8.2. Граф состояний многоканальной СМО с ограниченной очередью
Состояния данной системы означают:
S0 – отсутствие требований в системе;
S1 – одно требование обслуживается, очереди нет;
S2 – два требования обслуживаются, очереди нет;
…………………………………………………….
Sn – n требований обслуживаются, очереди нет;
Sn+1 – n требований обслуживаются, одно требование стоит в очереди;
…………………………………………………….
Sn+l – n требований обслуживаются, l требований стоят в очереди.
Система уравнений вероятностей состояний в стационарном режиме для цепочки S0 – Sn будет:

Для цепочки состояний Sn+1 – Sn+l система уравнений стационарного режима будет:

В качестве основных критериев, характеризующих качество функционирования рассматриваемой системы, выберем: 1) отношение средней длины очереди к наибольшему числу требований, находящихся одновременно в обслуживающей системе – коэффициент простоя обслуживаемого объекта; 2) отношение среднего числа незанятых обслуживающих каналов к их общему числу – коэффициент простоя обслуживаемого канала.
Рассмотрим расчет необходимых вероятностных характеристик (показателей качества функционирования) замкнутой СМО.
1. Вероятность того, что в системе находится k требований при условии, когда их число не превышает числа обслуживающих аппаратов п:
Pk=αkP0,
(1 k
k n),
n),
где
αk= или αk=
или αk=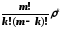 ;
;
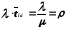 ;
;
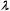 –
интенсивность
поступления требований в систему от
одного источника;
–
интенсивность
поступления требований в систему от
одного источника;
 об
– средняя продолжительность обслуживания
одного требования;
об
– средняя продолжительность обслуживания
одного требования;
т – наибольшее возможное число требований, находящихся в обслуживающей системе одновременно (m=n+l);
п – число обслуживающих аппаратов;
Р0 – вероятность того, что все обслуживающие аппараты свободны.
2. Вероятность того, что в системе находится k требований при условии, когда их число больше числа обслуживающих аппаратов:
Pk=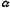 kP0,
(n
kP0,
(n k
k m),
m),
где
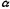 k=
k= (
(
 об)k
или αk=
об)k
или αk=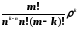 .
.
3. Вероятность того, что все обслуживающие аппараты свободны, определяется из условия
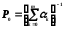
4. Среднее число требований, ожидающих начала обслуживания (средняя длина очереди):
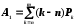 .
.
5. Коэффициент простоя требования в ожидании обслуживания:
a1=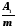 .
.
6. Вероятность того, что все обслуживающие аппараты заняты:
Pотк=
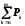 .
.
7. Среднее число требований, находящихся в обслуживающей системе (обслуживаемых и ожидающих обслуживания):
A2=
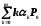 =
=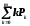 .
.
8. Коэффициент полного простоя требований на обслуживании и в ожидании обслуживания:
a2=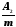 .
.
9. Среднее время простоя требования в очереди на обслуживание:
Tож=a1/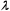 .
.
10. Среднее число свободных обслуживающих аппаратов:
A3= .
.
11 . Коэффициент простоя обслуживающих аппаратов:
a3
=
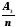 .
.
12. Вероятность того, что число требований, ожидающих обслуживания, больше некоторого числа В (вероятность того, что в очереди на обслуживание находится более В требований):
P-B
= =
=
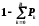 .
.
Рассмотрим пример расчета характеристик замкнутой СМО.
Пример 8.1. Оптовый склад строительных материалов обслуживает шесть предприятий-потребителей материалов. Каждый из потребителей направляет на склад автомашину за материалами в среднем один раз в смену (продолжительность смены 8 ч). На складе имеется один автопогрузчик, который используется только для погрузки материалов на прибывающие автомашины. Прибывшая на склад автомашина становится в очередь, если автопогрузчик занят погрузкой другой автомашины. Обработка статистических данных о продолжительности погрузки одной автомашины и проверка соответствующей гипотезы показали, что продолжительность погрузки одной автомашины подчиняется показательному закону распределения и составляет в среднем 48 мин (0,1 смены). Статистическое исследование потока автомашин показало, что число автомашин, поступающих на склад в единицу времени, подчиняется пуассоновскому закону распределения. Требуется провести расчет характеристик функционирования приведенной производственной системы как СМО.
Решение. Рассчитаем основные параметры системы для условий задачи.
Вероятность того, что все обслуживающие аппараты свободны (на складе нет автомашин) определяется как P0, λ=1, μ=0,1.
Вероятность того, что на складе одна автомашина:
P1=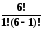 0,1P0=0,6P0,
0,1P0=0,6P0,
а вероятность того, что на складе две автомашины (одна под погрузкой, а другая в очереди):
P2=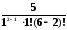 0,12P0=0,3P0.
0,12P0=0,3P0.
Рассчитывая аналогично, получим: Р3=0,12Р0; Р4=0,036Р0; Р5= 0,0072Р0; Р6 = 0,0007Р0. Так как сумма вероятностей нахождения системы в любом из состояний равна 1, т.е.
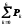 =1,
=1,
то P0(1 + 0,6 + 0,3 + 0,12 + 0,036 + 0,0072 + 0,0007) = 2,0639; Р0 = 1.
Отсюда находим Р0 = 0,4845.
Дальнейшие расчеты затруднений не вызывают. Например, средняя длина очереди равна
А1 =(2 - 1)Р2 + (3 - 1)Р3 + (4 - 1)Р4 + (5 - 1)Р5 + (6 - 1) Р6; А = 0,3296.
