Министерство образования и науки Российской Федерации

Федеральное агенство по образованию

Российский государственный профессионально-педагогический университет

Кафедра общей физики

4082

Математическая обработка результатов

физического эксперимента

Екатеринбург

2005

УДК 531

Учебно-методическая разработка

"Математическая обработка результатов физического эксперимента. Российский государственный проф.-пед. университет. Екатеринбург, 2005. 17с.

Составитель: доцент Литовский Владимир Васильевич,

Рецензент: д.ф.м.н., проф. П.С.Попель

В разработке приведены основные сведения по теории погрешностей для физического практикума. Особое внимание уделено оценкам случайных и систематических погрешностей. Отмечены отличительные особенности нахождения погрешностей электроизмерительных приборов. Приведены примеры округления численных значений физических величин.

Рассмотрено на заседании кафедры физики Протокол № 2 от 30.09.04

Заведующий кафедрой ОФ А.С.Борухович

Рекомендовано к печати методической комиссией ЭЭФ ИПИ Протокол №

от 21.03.2005 г.

Председатель методической комиссии В.Ф.Журавлев

 Российский государственный

профессионально-педагогический

университет, 2005

Измерения. Классификация погрешностей измерений

Одним из способов нахождения значения физической величины является ее измерение, т.е. опытное определение с помощью специальных технических средств - приборов и установок. Не все физические величины можно определить непосредственно прямыми измерениями, чаще всего искомое значение интересующей величины находят вычислением на основании известных зависимостей между ней и другими физическими величинами, определяемыми непосредственно из эксперимента. Соответственно, такие измерения называют прямыми и косвенными.

Следует учитывать, что никакое измерение не может быть выполнено абсолютно точно. Его результат содержит некоторую погрешность.

Погрешностью (абсолютной погрешностью) измерения называется разность

x-x₀ между результатом измерения x и истинным значением измеряемой величины x₀.

Относительная погрешность у – это отношение абсолютной погрешности

x-x₀ к истинному значению x₀ измеряемой величины: γ=(x-x₀)/x₀

Истинное значение измеряемой величины обычно неизвестно, потому в задачу измерении входит не только нахождение самой величины, но и оценка допущенной при измерении погрешности. .Для решения этой проблемы необходимо знать основные свойства погрешностей и методы их вычислений. Погрешность измерений можно разделить на три группы: промахи, случайные и систематические.

Промахи (грубые ошибки) возникают вследствие нарушения основных условий измерений. Например, при плохом освещении, регистрируя показания прибора вместо цифры 3 записали 8. Внешним признаком промаха является его резкое отличие по величине от остальных измерений. Такой результат необходимо отбросить, а измерение повторить.

Вычисление случайных и систематических погрешностей требует использование математических методов. Остановимся на них подробнее.

Случайные погрешности.

Случайными погрешностями называются погрешности, обусловленные неодинаковым действием совокупности физических факторов на измеряемую величину при повторении опытов.

Таким образом, наиболее существенным отличительным свойством случайной погрешности является непредсказуемость ее поведения при каждом повторном измерении. Так, при многократном определении линейного размера тела с помощью штангенциркуля из-за не идеальности его формы, поверхности, неодинаковой степени сжатия, неточности фиксации положения тела и т.д. результаты измерений будут отличаться друг от друга случайным образом. Следует отметить, что случайные величины возникают вследствие самых различных причин, результаты, действия которых столь малы, что их нельзя учесть по отдельности. Поэтому их рассматривают как суммарный эффект множества физических факторов и учитывают с помощью методов теории вероятностей.

Ясно, что при многократном повторении опыта экспериментатора интересует наиболее вероятное значение определяемой величины. Если каждое из полученных значений случайной величины x_i повторяется один раз, то относительная частота Р_i (вероятность) его появления определяется как (1/N) и за наиболее вероятное значение

(1)

вполне можно принять среднеарифметическое значение

(2)

вытекающее из выражения (1). При различной частоте выпадения случайной величины x_i P_i=(m_i/N) необходимо пользоватьсяобщей формулой (1) (m_i - число повторений cлучайной величины x_i ).

Если построить зависимость числа попаданий ΔN случайной величины x_i в определенный интервал dx отрезка [а, б] при достаточно большом числе измерений N, то отношение ΔN/N будет определять относительную частоту (вероятность) dP(x) попаданий указанной величины х в интервал dx :

Для оценки случайной погрешности важно знать значение вероятностей dP(x) в пределах всего отрезка [а,б], т.е. функцию распределения вероятностей ∫(x), определяемую соотношением или и называемую иначе плотностью вероятности (по аналогии с понятием плотности известным из механики).

Эта функция в общем случае имеет сложный вид и удовлетворяет двум очевидным требованиям:

1)

2)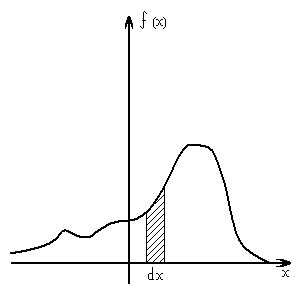

П

Рис.1

ервое из них констатирует тот факт, что вероятность любого события всегда положительна, а второе - что бесконечное увеличение интервала возможных значений случайной величины х приводит к неизбежности появления этого события. Графический смысл функции распределения состоит в том, что элемент площади под ее кривой определяет вероятность появления случайной величины в интервале dx.

Функция распределения вероятности позволяет определить две

основные характеристики распределения случайной величины – ее среднее значение (математическое ожидание) и среднеквадратичное отклонение (или стандарт).

Среднее значение (математическое ожидание) случайной величины определяется естественным образом выражением

(3)

которое предполагает "взвешивание" каждой из величин х бесконечного интервала соответствующей вероятностью dР(х), так, что суммирование "взвешенных" значений х по всему интервалу обеспечивает средневзвешенное значение ∫(x) . При переходе к дискретному (от латинского discretus - разделенный, прерывистый) числу измерений (x₁, x₂, …, x_N) функцию распределения и соответственно dP(х) нужно считать отличными от нуля только в этих точках (∫(x_i) P(x_i)), и интеграл заменить суммой т.е.

Так, что получаем уже известное выражение x_0.

В частности, если ∫(х) отлична от нуля в точках x₁=1, x₂=2, x₃=3, x₄=4, x₅=5, а соответствующие им вероятности P₁=0,025; P₂=0,05; P₃=0,085; P₄=0,1; P₅=0,125, то средневзвешенным окажется x₀=3=x₃

Для характеристики распределения случайных величин необходимо также определить величину, являющуюся мерой их разбросанности возле среднего значения. Если за такую меру принять сумму разностей между каждой из случайных величин x_i и их средним значением, умноженных на соответствующие вероятности, то при значительном расширении интервала x_i будет стремиться к нулю и, следовательно, не даст желаемого результата.

Например, для указанных выше х_i и Р_i имеем:

Наиболее разумной оценкой такого разброса может служить сумма квадратов разностей (x_i-x₀)² с учетом вероятности реализации каждой из них. При непрерывном распределении случайных величин вдоль бесконечного интервала эту меру определяют следующим образом

(4)

D(x) - называют дисперсией случайной величины х. Сопоставляя выражение (4) с формулой (3), легко понять, что дисперсия определяет средневзвешенное значение (x-x₀)² - их возможных разностей (x-x₀)², умноженных на соответственные вероятности.

Обращаясь к приведенному выше примеру, имеем:

т.е. D(x)≠0 и, следовательно, может быть принята за меру определения погрешностей случайных величин.

В действительности, удобнее всего пользоваться среднеквадрати-ческим отклонением случайной величины х, определяемым как корень квадратный от дисперсии этой величины,

(5)

Из выражения (5) видно, что в точности совпадает по размерности с исследуемой случайной величиной х и, следовательно, вполне может быть принята за меру погрешности ее определения.

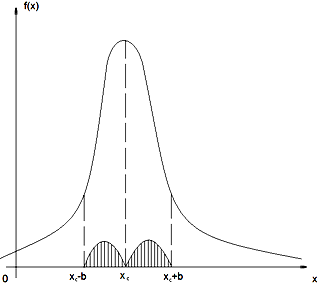
Анализ поведения распределения многих физических величин приводит к так называемому нормальному рас­пределению (распределению Гаусса) случайной величины х, для которого плотность вероятности имеет вид:

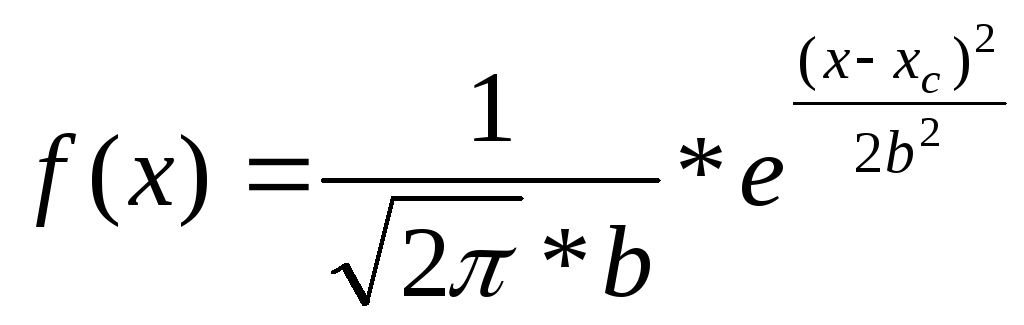(6)

Э

Рис. 2

та функция симметрична относительно значения х_с ,а ее параметр b определяет крутизну пика f(х) , т.е. меру разброса случайных значений х возле некоторого значения х_с.

Можно убедиться, что входящие в формулу (6) параметры "х_с" и "b" есть ничто иное, как среднее значение x₀ и среднеквадратичное отклонение δ(x).

Зная x₀ и δ(x) для нормального распределения случайной величины х можно составить себе приближенное представление о диапазоне ее возможных значений. А именно, значения случайной ве­личины х лишь изредка выходят за пределы интервала x₀ ± 3δ(х) и с вероятностью > 99% можно считать, что они укладываются в этот интервал. В интервал x₀ ± 2δ(х) попадает 95 % случайных величин.

Вероятность попадания результатов в заданный интервал х называется доверительной вероятностью и обозначается буквой α , а сам интервал называется доверительным.

На практике для определения той или иной физической величины проводят конечное число её измерений. Поэтому при определении x₀ и δ(x)приходиться пользоваться их приближенными выражениями (оценками) из имеющегося конечного числа значений x_i.

Разумным приближением x₀ может служить среднеарифметичес­кое значение , которое, как было показано выше при условии равно вероятности каждого из x_i закономерно следует из (I).

Для дисперсии D(x)=δ² на первый взгляд наиболее естественной представляется оценка в виде:

где x_i - независимые случайные величины.

Более точный математический анализ показывает , что истинное значение дисперсии D(х) связано выражением:

(7)

Соответственно точное значение среднеквадратичного отклонения равно:

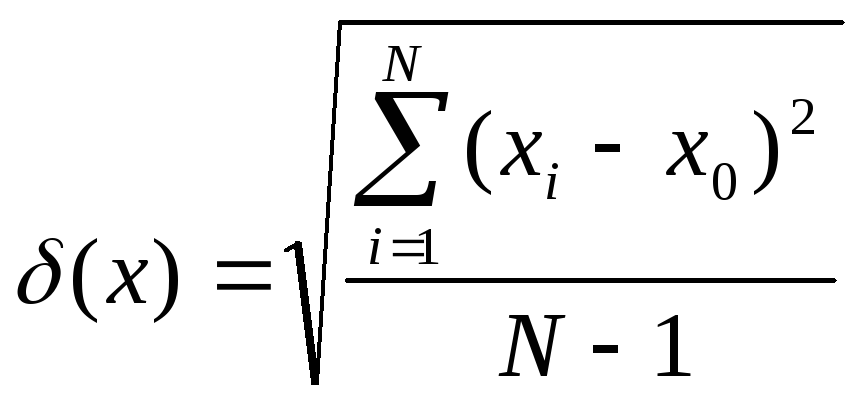(8)

Можно заметить, что введение поправочного множителя играет заметную роль лишь при малых N и теряет смысл при больших его значениях.

Таким образом, в реальных расчетах вполне уместно пользоваться приближенными значениями x₀ и D(x), при этом делая соответствующую поправку для.

Отметим, что оценка будучи функцией случайных величин сама является случайной величиной, поэтому пользуясь ею мы всегда совершаем какую-то ошибку. Для того, чтобы ее оценить рассмотрим дисперсию (не путать ). Для этого будем рассматривать как функцию независимых случайных величин, считая при этом что каждая из величин x_i распределена по одинаковому закону распределения, т.е. . Действительно, поскольку точки x_i - случайны, т.е. появление x_i не обязательно влечет появление х_i, то их можно считать незави­симыми, и полагать, что при большом числе испытаний каждая из х_i и х_i дает набор значений, подчиняющийся закону нормального распределения, справедливого для любой из рассматриваемых случайных величин х₁,х₂,…,х_N.

Вспоминая, что

,

имеем

или с учетом того, что и ,

т.е. ,

имеем

для дисперсии

Подставляя связь истинного значения дисперсии для произвольной случайной величины х_i с ее оценкой , окончательно получаем:

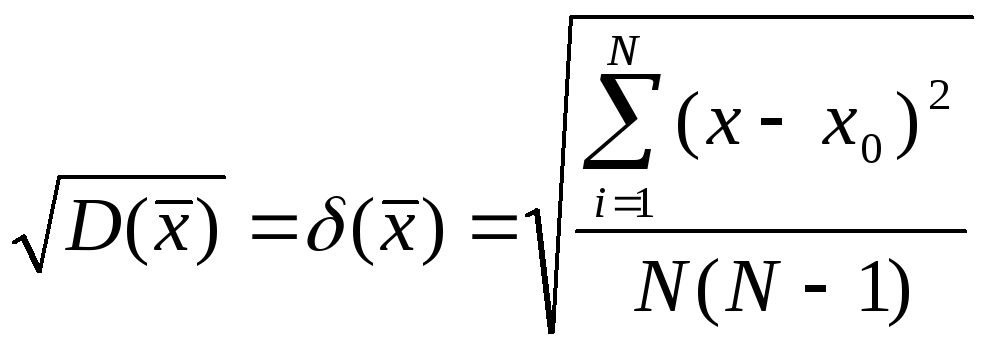(9)

или (10)

Выше было показано, какими оценками, исходя из реальных возможностей экспериментатора, необходимо пользоваться для случайных величин, подчиняющихся закону нормального распределения. Было отмечено, что данный закон справедлив для большого числа измерений N и выявлено, что истинное значение случайной величины х с вероятностью Р=0,95 попадает в интервал ±2δ(х) от среднеарифметического значения х.

Однако при малых значениях числа измерений N функция нормального

распределения для оценки вероятности попадания случайной величины х в определенный интервал dх не является точной и, следовательно, пользуясь ею мы совершаем некоторую погрешность в определении указанного интервала.

Этого можно избежать, если воспользоваться распределением Стьюдента*¹.

Данное распределение обладает тем свойством, что позволяет точно находить вероятность попадания случайной величины х при наличии ограниченного числа ее значений и экспериментальной дисперсии* , а при больших N переходит в нормальное (см. рис.3).

*

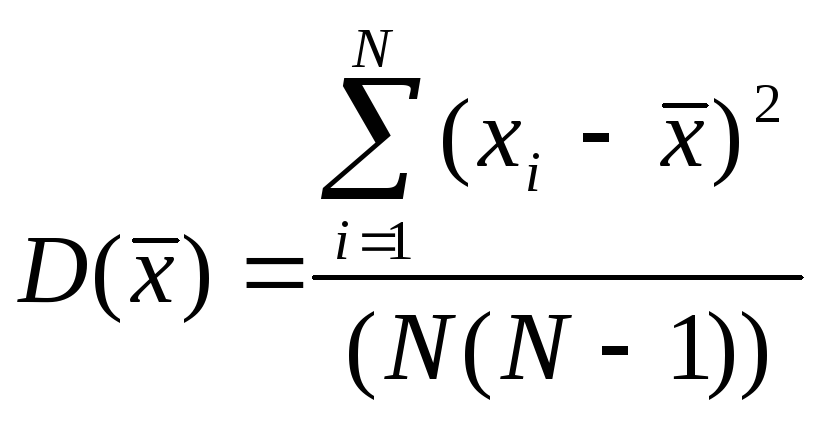
Распределение Гаусса

Распределение Стъюдента

Рис.6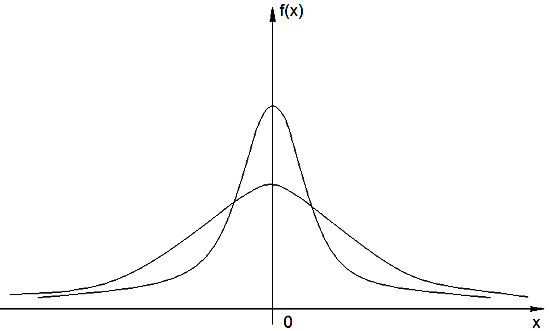

При малых N пользуясь этим распределением можно вычислить доверительный интервал, при заданной вероятности Р, попадания в него среднеарифметического значения

Сопоставляя этот интервал с интервалом, рассчитанным в тех же предположениях при нормальном распределении случайной величины х для каждого из значений N можно найти уточняющий множитель t_P,N для интервала, соответствующего нормальному распределению. Этот множитель называют коэффициентом Стъюдента¹ и представляют в табличном виде. Например, для Р=0,95 значения t_0,95;N равны:

N	3	4	5	6	7	8	9	10	…. 20
t0,95;N	4.30	3.18	2.77	2.57	2.45	2.36	2.31	2.26	2.09

Видно, что по мере увеличения числа измерений t_P,N→2 и соот­ветственно доверительный интервал укладывается в пределы . Таким образом, для ограниченного числа измерений среднеарифметическое значение определяется со случайной погрешностью или для границы интервала : имеем:

(11)

^{____________________________}