Уральская Государственная Архитектурно-Художественная Академия

Институт Урбанистики

Лабораторная работа №2

Построение функции принадлежности

Принятие решений в условиях неопределенности

Выполнили: ст-ты гр. 504

Еремеева Н. Ю.

Калимулина А. Р.

Таушканова М.А.

Проверил: Клюкин В.Э.

г.Екатеринбург, 2009 г.

Оглавление

Построение функции принадлежности методом парных сравнений 3

Задача №1. Вычисление функции принадлежности методом парных сравнений. 4

Принятие решений в условии неопределенности 9

Задача №2. Использование нечетких множеств, при условии существования критериев одинаковой важности. 10

Задача №3. Использование нечетких множеств, при условии существования критериев различной важности. 12

Построение функции принадлежности методом парных сравнений

α=µ*n

где n - число альтернатив, или число критериев, по которым определяется важность.

Пусть Х - некоторое четкое множество от 1 до n.

Пусть Ã - нечеткое множество над Х, функция µ для которого пока не известна.

Пусть матрица Ã состоит из некоторых чисел a1,a2,...,an, которые получены путем парных сравнений.

Сравнение альтернатив по некоторому критерию (i-я альтернатива сравнивается с j-й)

Оценка важности	Качественная оценка	Примечание
1	Одинаковая значимость	По данному критерию альтернативы i и j имеют одинаковый ранг. (<0.9/a1>,<0.9/a2>) - 0.9 одинаковый ранг
3	Слабое превосходство	Соображения о предпочтении одной альтернативы перед другой малоубедительны.
5	Превосходство	Имеются надежные доказательства превосходства одной альтернативы перед другой
7	Очевидное превосходство	Существуют убедительные свидетельства в пользу одной альтернативы.
9	Абсолютное превосходство	Противоположной альтернативой можно просто пренебречь.

Пусть после попарного сравнения альтернатив i и j получилась матрица:

А^↔=|a_ij|={λ₁, λ₂, λ₃, λ₄}

А^↔W=λW, где λ - собственное значение матрицы

Для каждого значения λ можно найти значение, зависящее как от самой матрицы, так от вектора, который нужно найти.

W^→_i=ƒ(A^↔,λ_i)= µ*n

 

Функции, которые используются в Mathcad:

eiginval(A^↔)=λ

eiginvec(A^↔,λ_n)

W_n^→={w₁,w₂,…,w_n}

Задача №1. Вычисление функции принадлежности методом парных сравнений.

Условие.

Пусть имеется некоторый источник света. Для нахождения различий в освещенности 4-х одинаковых объектов в зависимости от расстояния от источника был проведен следующий эксперимент: посадили 2 группы людей и попросили их оценить освещенность для предметов, установленных на следующем расстоянии от источника:

Х1 =	9 м
Х2 =	15 м
Х3 =	21 м
Х4 =	28 м

Первая группа получила следующую матрицу А1:

	а1	a2	a3	a4
a1	1	5	6	7
a2	^1/5	1	4	6
a3	^1/6	^1/4	1	4
a4	^1/7	^1/6	^1/4	1

Вторая группа получила следующую матрицу А2:

	а1	a2	a3	a4
а1	1	4	6	7
a2	^1/4	1	3	4
a3	^1/6	^1/3	1	2
a4	^1/7	^1/4	^1/2	1

Решение.

Для решения данной задачи используем программу Mathcad, которая в полной степени позволит добиться точных результатов и верного ответа для поставленной задачи. Mathcad содержит функции для обычных в линейной алгебре действий с массивами. Эти функции предназначены для работы с векторами и матрицами. В Mathcad существуют функции eigenvals и eigenvec для нахождения собственных значений и собственных векторов матрицы этих значений.

1. Записываем две матрицы, которые получили группы при сравнении освещенности предметов.

Для этого в любой точке поля записываем А1:= , затем на панели инструментов выбираем вкладку «Insert» → «Matrix». В появившемся диалоговом окне выбираем необходимое количество строк и столбцов данной матрицы, в нашем случае Rows(строк)=4 и Columns(столбцов)=4

После вставки матрицы необходимо заполнить каждую ячейку конкретным числом. Для построения второй матрицы А2 проделываем те же самые действия.

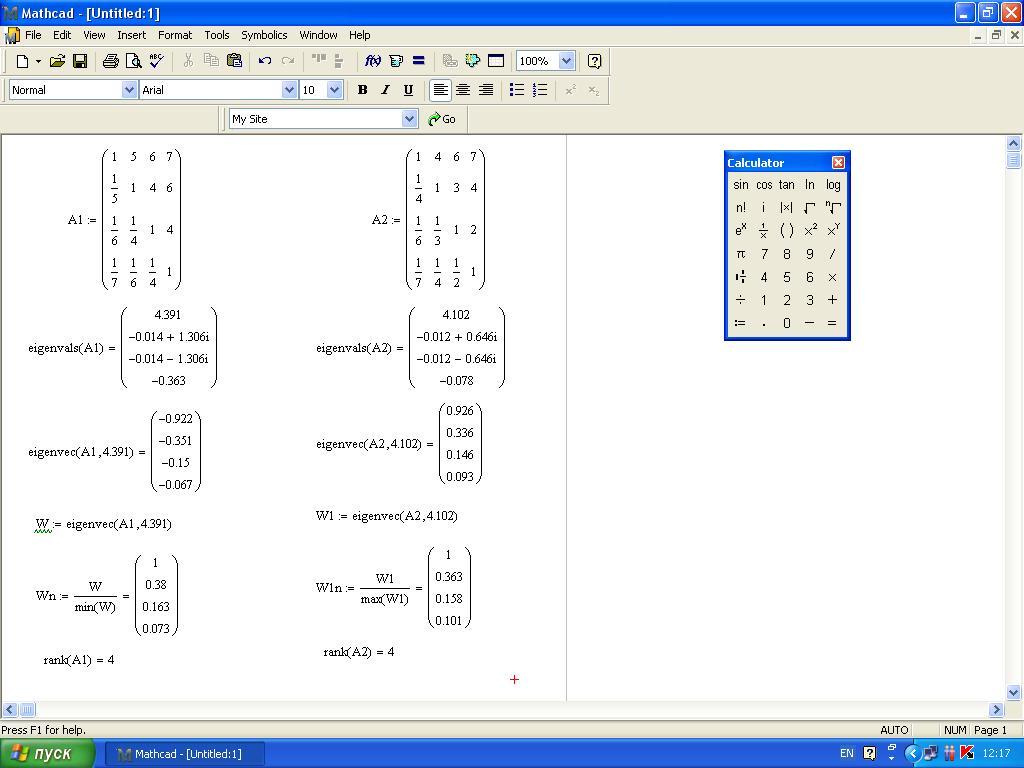
2. Находим для каждой матрицы вектор ее собственных значений. Для этого используем функцию eigenvals, которая возвращает вектора, чьи значения являются собственными значениями для каждой из матриц.

Для этого выбираем вкладку «Insert»→ «Function».

После чего появляется диалоговое окно «Insert Function», в левой его части (Function Category) выбираем категорию «Vector and Matrix», а в правой части (Function Name) выбираем функцию: eigenvals. Нажмем ОК.

После ввода имени нужной матрицы (eigenvals(A1) или eigenvals (A2)) и знака «=» программа автоматически выдает значения вектора.

3. Находим для каждой матрицы собственные вектора максимальных собственных значений.

Для этого используем функцию eigenvec, которая возвращает собственные вектора, связанные с собственными значениями z1 и z2 матриц А1 и А2 соответственно. Максимальное значение z1 матрицы А1 равно 4.391, а максимальное значение z2 матрицы А2 равно 4.102.

Для нахождения функции eigenvec необходимо во вкладке «Insert»→ «Function» выбирать функцию: eigenvec. На место первого параметра вводим обозначение матрицы, а на место второго параметра вводим соответствующие этой матрице ее максимальное собственное значение вектора.

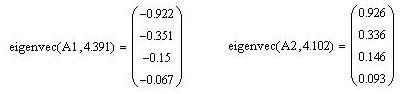
Обозначим через W и W1 нахождение функции eigenvec() для матрицы А1 и А2 соответственно.

4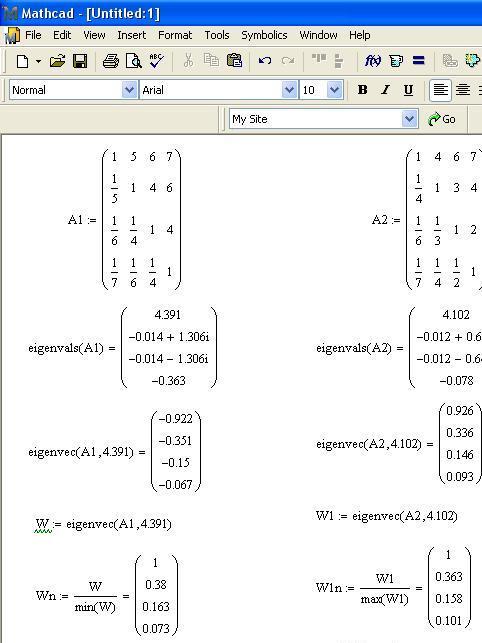. Необходимо нормировать значения собственных векторов матриц А1 и А2. Для этого с помощью инструмента «Calculator» во вкладке меню «View»→ «Toolbars» записываем следующие формулы:

Wn:=W/min(W) W1n:=W1/max(W1)

Р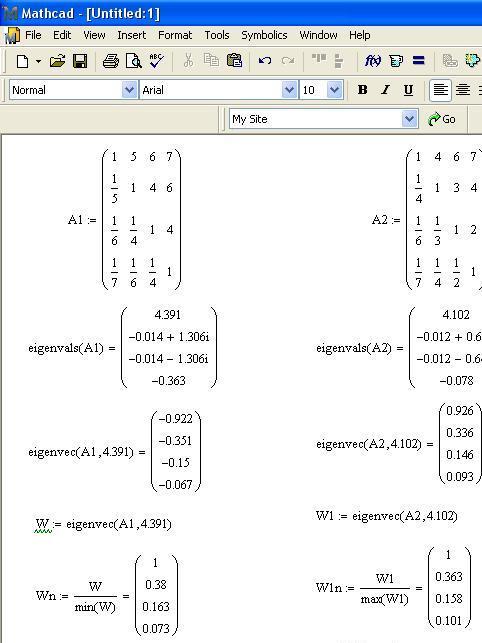езультат нормировки:

5. Получаем ранг матриц А1 и А2, используя функцию rank - нахождение ранга вещественной матрицы, из вкладки «Insert»→ «Function».

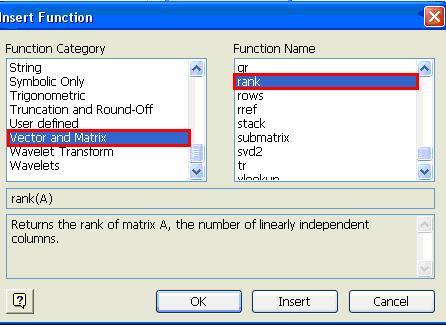
Ранги матриц равны 4. Rank(A1)=4 и rank(A2)=4

Вывод.

На основе выполненной работы можно сделать вывод, что чем ближе значение λn к рангу матрицы n, тем более профессионально проведена экспертиза. Таким образом, наиболее профессиональную экспертизу по сравнению освещенности каждого предмета провела вторая группа (ее максимальное собственное значение полученной матрицы равное 4.102 более близкое к рангу матрицы, равному 4).