
-
Расчет линейной модели.
Записываем уравнение процесса в виде:
Y=b0+b1x1+b2x2+b3x3+…+b1..kx1×..×xk (1)
Коэффициенты линейной модели вычисляются по формуле:
bj
=
![]() . (2)
. (2)
где, b0 есть среднее арифметическое значений параметра оптимизации.
Проведем расчеты, получим следующие коэффициенты:
b0=0,153, b1= 0,002, b2=0,025, b3=0,013, b4= 0,0104.
Тогда уравнение процесса запишется в виде:
Y=0,153 + 0,002х1 + 0,025х2 + 0,013х3 + 0,0104х4.
Ошибка, возникающая из-за несовпадения результатов при проведении параллельных опытов определяется по следующим показателям:
а). Среднее арифметическое значение параметра оптимизации:
![]() =
(y1
+ y2
+ y3
+ . . . +
yn)
/ n =
=
(y1
+ y2
+ y3
+ . . . +
yn)
/ n =
![]() (3)
(3)
где уi - результаты экспериментов, n - количество опытов в серии.
![]() 1=0,123
1=0,123
![]() 5=0,1375
5=0,1375
![]() 9=0,0575
9=0,0575
![]() 13=0,105
13=0,105
![]() 2=0,065
2=0,065
![]() 6=0,105
6=0,105
![]() 10=0,195
10=0,195
![]() 14=0,235
14=0,235
![]() 3=0,1975
3=0,1975
![]() 7=0,225
7=0,225
![]() 11=0,16
11=0,16
![]() 15=0,2025
15=0,2025
![]() 4=0,1725
4=0,1725
![]() 8=0,115
8=0,115
![]() 12=0,15
12=0,15
![]() 16=0,2025
16=0,2025
б) Дисперсия - среднее значение квадрата отклонений величины от ее среднего значения:
![]() ,
(4)
,
(4)
где (n-1) - число степеней свободы, равное количеству параллельных опытов минус единица.
Дисперсия имеет следующие значения:
S21=0,000234 S25=0,000292 S29 =0,000292 S213 =0,000166
S22=0,000166 S26=0,000166 S210 =0,000166 S214 =0,0007
S23=0,000292 S27=0,000166 S211 =0,000335 S215 =0,000756
S24=0,000225 S28=0,000166 S212 =0,000335 S216 =0,000292
в). Квадратичная ошибка вычисляется по формуле:
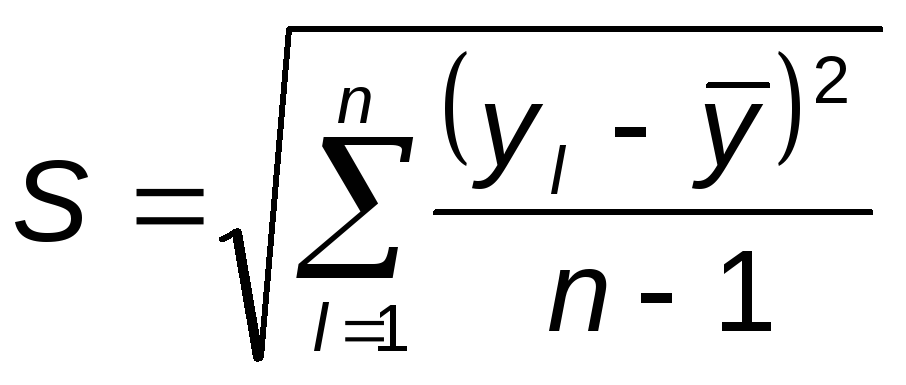 . (5)
. (5)
подставив значения результатов эксперимента и их среднее арифметическое в (5) получим следующие значения квадратичной ошибки:
S1=0,0153 S5 =0,0171 S9 =0,0171 S13 =0,0129
S2=0,0129 S6=0,0129 S10 =0,0129 S14 =0,0265
S3=0,0171 S7=0,0129 S11 =0,0183 S15 =0,0275
S4=0,01 5 S8=0,0129 S12 =0,0183 S16 =0,0171
Для определения ошибок опыта используем критерий Стьюдента:
![]() , (6)
, (6)
где t – табличное значение критерия Стьюдента,
Учитывая,
что t=4.3
, запишем неравенство
![]() .
.
Полученные дисперсии проверяем на однородность с помощью критерия Фишера. Для этого найдем отношение большей дисперсии к меньшей и полученную величину сравним с табличной равной 9,3
![]()
Критерий Фишера, полученный расчётным путём меньше табличного значения, значит дисперсии однородны.
Рассчитаем дисперсию параметра оптимизации по формуле:
 , (7)
, (7)
где fi =n-1 –число степеней свободы в i-м опыте.
Число степеней свободы дисперсии параметра оптимизации принимается равной сумме чисел степеней свободы дисперсий из которых она вычислена.
Тогда дисперсия параметра оптимизации: S2y=0,0003.
3. ОЦЕНКА АДЕКВАТНОСТИ МОДЕЛИ.
После построения модели необходимо провести проверку ее адекватности.
С этой целью вычисляем дисперсию адекватности по формуле:
![]() , (8)
, (8)
где
![]() -
значение параметра оптимизации полученное
по линейной модели.
-
значение параметра оптимизации полученное
по линейной модели.
Значения параметра оптимизации:
![]() 1=0,1025
1=0,1025
![]() 5=0,1285
5=0,1285
![]() 9=0,1233
9=0,1233
![]() 13=0,1493
13=0,1493
![]()
![]() 2=0,1065
2=0,1065
![]() 6=0,1325
6=0,1325
![]() 10=0,1273
10=0,1273
![]() 14=0,1533
14=0,1533
![]() 3
= 0,1527
3
= 0,1527
![]() 7=0,1787
7=0,1787
![]() 11=0,1735
11=0,1735
![]() 15=0,1995
15=0,1995
![]() 4=0,1567
4=0,1567
![]() 8=0,1827
8=0,1827
![]() 12=0,1775
12=0,1775
![]() 16=0,2035
16=0,2035
![]() Число
степеней свободы вычисляется по следующей
формуле:
Число
степеней свободы вычисляется по следующей
формуле:
f=N-(k+1), (9)
где N – число серий опытов, k - количество факторов.
Получим, f=16-(4+1)=11.
Подставив полученные значения в формулу (8), получим значение дисперсии адекватности:
S2ад=0,0028.
Для проверки адекватности модели используется Ф-критерий Фишера, который определяется следующей формулой:
F
= Sад2
/
![]() .
(10)
.
(10)
Расчетное значение критерия Фишера F=9.236, табличное значение F=1.8.
9.236>1.8
Равенство означает, что модель неадекватна.
Проверим значимость каждого коэффициента. Для этого рассчитаем дисперсию коэффициента регрессии по формуле:
S2{bj} = Sy2 / N. (11)
S2{bj} =0,00002
На основе полученной дисперсии коэффициентов регрессии строим доверительный интервал по формуле:
Dbj = ±t×S{bj}, (12)
где S{bj} - квадратичная ошибка коэффициента регрессии; t - табличное значение критерия Стьюдента.
Dbj =±2*0,00447=±0,0089
Коэффициент является значимым, если его абсолютная величина больше доверительного интервала. Коэффициент b1 не является значимым, т.к. |0,002|<0,0089.
