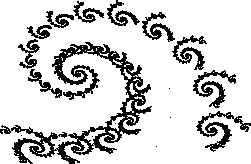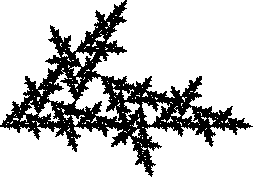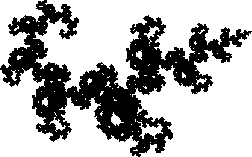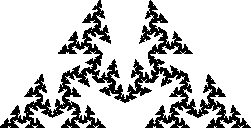Лабораторная работа №9. Построение фракталов, задаваемых системой итеративных функций.
Цель работы: Изучение и программная реализация алгоритмов построения фракталов, задаваемых системами итеративных функций (СИФ).
Теоретическая часть.
Определение. Линейное преобразование вместе с последующим преобразованием сдвига будем называть аффинным преобразованием.
Аффинное
преобразование
в
пространстве
можно
представить в матричной форме:
Важное свойство аффинного преобразования заключается в том, что аффинное преобразование отрезок переводит в отрезок.
Аффинное
преобразование плоскости однозначно
определяется тройкой не лежащих на
одной прямой точек и их образами. В самом
деле, пусть некоторое АП
отображает
точки
,
,
в
точки
,
и
.
Тогда имеем:
Если
то получаем следующую систему линейных уравнений:
Или, переписывая, получаем:
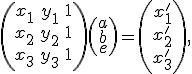
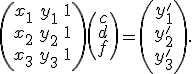
Решая эту систему, находим матричное представление аффинного преобразования.
Системе
итерируемых функций в пространстве
:
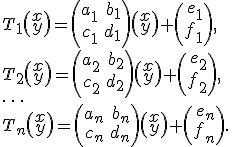
соответствует следующий формат представления:
Fractal {
a1 b1 c1 d1 e1 f1 p1
a2 b2 c2 d2 e2 f2 p2
..............
an bn cn dn en fn pn
}
где числа
есть
вероятности выбора соответствующих
преобразований в рандомизированном
алгоритме.
Для построения фракталов, задаваемых таким способом требуется в программе описать процедуру изменения координат по задаваемому коэффициентами СИФ закону.
Пример. Написать программу построения фрактала Лист, задаваемого следующим набором СИФ:
|
Leaf_3 { 0.60 -0.6 0.6 0.60 0.00 0.0 0.5 0.53 0.0 0.0 0.53 0.47 0.0 0.5 }
|
Рис. Фрактал Лист. |
program Leaf_3;
uses CRT, Graph;
var
gd,gm : Integer;
const
iter = 50000;
procedure Draw;
var
t, x, y, p : Real;
k : LongInt;
mx, my, rad : Integer;
begin
mx := 10;
my := 250;
rad :=600;
Randomize;
x := 0.0;
y := 0.0;
for k := 1 To iter do
begin
p := Random;
t := x;
if p <= 1/2 then
begin
x := 0.6 * x -0.6* y;
y := 0.6 * t +0.6* y;
end
else
begin
x := 0.53 * x +0.0 * y +0.47;
y := 0.0* t +0.5 * y;
end;
PutPixel(mx + Round(rad * x), my - Round(rad * y), 2);
end;
end;
begin
gd := Detect;
InitGraph(gd,gm,'d:\bp\bin');
Draw;
ReadKey;
CloseGraph;
end.
Задания для индивидуальной работы.
Создать программу построения фрактала, задаваемого СИФ (по вариантам).
|
№ |
СИФ |
Вид готового изображения |
|
|
Dragon { 0.824074 0.281482 -0.212346 0.864198 -1.882290 -0.110607 0.787473 0.088272 0.520988 -0.463889 -0.377778 0.785360 8.095795 0.212527 }
|
|
|
|
Spiral_1 { 0.787879 -0.424242 0.242424 0.859848 1.758647 1.408065 0.895652 -0.121212 0.257576 0.151515 0.053030 -6.721654 1.377236 0.052174 0.181818 -0.136364 0.090909 0.181818 6.086107 1.568035 0.052174 }
|
|
|
|
Swirl { 0.745455 -0.459091 0.406061 0.887121 1.460279 0.691072 0.912675 -0.424242 -0.065152 -0.175758 -0.218182 3.809567 6.741476 0.087325 }
|
|
|
|
Zigzag_2 { -0.632407 -0.614815 -0.545370 0.659259 3.840822 1.282321 0.888128 -0.036111 0.444444 0.210185 0.037037 2.071081 8.330552 0.111872 }
|
|
|
|
Binary { 0.5 0.0 0.0 0.5 0.0 0.0 0.333333 0.5 0.0 0.0 0.5 0.5 0.0 0.333333 0.0 -0.5 0.5 0.0 1.0 0.5 0.333333 }
|
|
|
|
Leaf { 0.14 0.01 0.00 0.51 -0.08 -1.31 0.06 0.43 0.52 -0.45 0.50 1.49 -0.75 0.37 0.45 -0.49 0.47 0.47 -1.62 -0.74 0.36 0.49 0.00 0.00 0.51 0.02 1.62 0.21 }
|
|
|
|
Fern { 0.00 0.00 0.00 0.16 0.00 0.00 0.01 0.85 0.04 -0.04 0.85 0.00 1.60 0.85 0.20 -0.26 0.23 0.22 0.00 1.60 0.07 -0.15 0.28 0.26 0.24 0.00 0.44 0.07 }
|
|
|
|
Dendrit_1 { 0.5 0.5 0.5 -0.5 0.0 0.0 0.5 0.6 -0.2 -0.2 -0.6 0.4 0.2 0.5 }
|
|
|
|
Wolfs { 0.5 0.5 -0.5 0.5 -1.0 0.0 0.5 0.5 0.5 0.5 -0.5 0.0 1.0 0.5 }
|
|
|
|
Spiral_12 { -0.61 0.7 -0.7 -0.61 0.00 0.0 0.9 0.21 0.0 0.0 0.21 0.79 0.0 0.1 }
|
|
|
|
Talon { 0.7 0.2 -0.2 0.7 0.0 0.0 0.5 0.0 -0.6 0.6 0.0 1.0 -0.6 0.5 }
|
|
|
|
Frog_paws { -0.4 0.51 -0.51 -0.4 0.0 0.00 0.5 -0.4 -0.51 0.51 -0.4 1.4 -0.51 0.5 }
|
|
Контрольные вопросы
-
Опишите формат представления СИФ и систему линейных уравнений, ему соответствующую.
-
Запишите фрагмент кода программы для построения фракталов, задаваемых СИФ.
Лабораторная работа №10.
Построение геометрических фракталов.
Цель работы: Изучение и программная реализация алгоритмов построения геометрических фракталов.
Теоретическая часть.
1. Снежинка Коха
Строится она на основе равностороннего треугольника. Каждая линия которого ___ заменяется на 4 линии каждая длинной в 1/3 исходной _/\_. Таким образом, с каждой итерацией длинна кривой увеличивается на треть. И если мы сделаем бесконечное число итераций - получим фрактал - снежинку Коха бесконечной длинны.
Построение кривой Коха
Процесс
построения кривой Коха выглядит следующим
образом: берём единичный отрезок,
разделяем на три равные части и заменяем
средний интервал равносторонним
треугольником без этого сегмента. В
результате образуется ломанная, состоящая
из четырёх звеньев длины
.
На следующем шаге повторяем операцию
для каждого из четырёх получившихся
звеньев. Предельная кривая и есть кривой
Коха.
Кривую Коха можно также построить с помощью двух СИФ-преобразований:
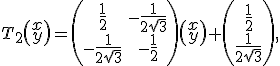
В формате FRACTINT эти преобразования запишутся следующим образом:
Curve_Koch {
0.5 0.288675 0.288675 -0.5 0 0 0.5
0.5 -0.288675 -0.288675 -0.5 0.5 0.288675 0.5
}
program Koh;
uses CRT, Graph;
var
gd,gm : Integer;
const
iter = 50000;
procedure Draw;
var
t, x, y, p : Real;
k : LongInt;
mx, my, rad : Integer;
begin
mx := 10;
my := 250;
rad :=600;
Randomize;
x := 0.0;
y := 0.0;
for k := 1 To iter do
begin
p := Random;
t := x;
if p <= 1/2 then
begin
x := 1/2 * x + 1/(2*sqrt(3)) * y;
y := 1/(2*sqrt(3)) * t - 1/2 * y;
end
else
begin
x := 1/2 * x - 1/(2*sqrt(3)) * y +1/2;
y := -1/(2*sqrt(3)) * t - 1/2 * y + 1/(2*sqrt(3));
end;
PutPixel(mx + Round(rad * x), my - Round(rad * y), 2);
end;
end;
begin
gd := Detect;
InitGraph(gd,gm,'');
Draw;
ReadKey;
CloseGraph;
end.
Кривая Коха имеет бесконечную длину. Кроме того, кривая Кох состоит из четырёх равных частей, каждая из которых подобна всей кривой с коэффициентом подобия 1/3. Отсюда следует, что каждая часть кривой имеет бесконечную длину. Также эта кривая нигде себя не пересекает, так как достраиваемые треугольники каждый раз достаточно малы и никогда не "сталкиваются" друг с другом.