Задания для индивидуальной работы.

1. Реализовать один из описанных геометрических фракталов с помощью СИФ (по вариантам).

2. Реализовать построение треугольника Серпинского или драконовой кривой (по вариантам) описанным геометрическим способом.

Контрольные вопросы.

1. Опишите геометрический алгоритм построения фрактала снежинка Коха.

2. Опишите геометрический алгоритм построения фрактала треугольник Серпинского.

3. Опишите геометрический алгоритм построения фрактала кривая дракона.

4. Запишите СИФ, соответствующую фракталу снежинка Коха.

5. Запишите СИФ, соответствующую фракталу треугольник Серпинского.

6. Запишите СИФ, соответствующую фракталу кривая дракона.

Лабораторная работа №11. Построение алгебраических фракталов.

Цель работы: Изучение и программная реализация алгоритмов построения алгебраических фракталов.

Теоретическая часть.

Свое название они получили за то, что их строят, на основе алгебраических формул. Методов получения алгебраических фракталов несколько. Один из методов представляет собой многократный (итерационный) расчет функции Zn+1=f(Zn), где Z - комплексное число, а f некая функция. Расчет данной функции продолжается до выполнения определенного условия. И когда это условие выполнится - на экран выводится точка. При этом значения функции для разных точек комплексной плоскости может иметь разное поведение:

1. С течением времени стремится к бесконечности.

2. Стремится к 0

3. Принимает несколько фиксированных значений и не выходит за их пределы.

4. Поведение хаотично, без каких либо тенденций.

Множество Мандельброта.

Для его построения необходимы комплексные числа. Комплексное число - это число, состоящее из двух частей - действительной и мнимой, и обозначается оно a+bi.

Множество всех точек , для которых итерации остаются ограниченными при , называется множеством Мандельброта

Приняв, что и , раскладывая на действительную и мнимую часть, получаем:

Цвет обычно выбирают по числу итераций, но есть и другие способы.

Пример. Построение множества Мандельброта.

program M2;

uses Graph, Crt;

type

TComplex = record

x : Real;

y : Real;

end;

const

iter = 50;

max = 16;

var

z, t, c : TComplex;

x, y, n : Integer;

Cancel : Boolean;

gd, gm : Integer;

mx, my : Integer;

begin

Cancel := False;

Randomize;

gd := Detect;

InitGraph(gd,gm,'e:\bp\bgi');

Mx := GetMaxX div 2;

My := GetMaxY div 2;

for y := -my to my do

for x := -mx to mx do

begin

n := 0;

c.x := x * 0.005;

c.y := y * 0.005;

z.x := 0;

z.y := 0;

while (sqr(z.x) + sqr(z.y) < max) and (n < iter) do

begin

t := z;

z.x := sqr(t.x) - sqr(t.y) + c.x;

z.y := 2 * t.x * t.y+ c.y;

Inc(n);

if KeyPressed then

Cancel := true;

end;

if n < iter then

begin

PutPixel(mx + x,my + y,16 - (n mod 16));

end;

if Cancel then

exit;

end;

Readkey;

CloseGraph;

end.

Изменяя значение n в общей формуле, можно получать различные варианты изображения.

3. Фрактал Ньютона

Области с фрактальными границами появляются при приближенном нахождении корней нелинейного уравнения алгоритмом Ньютона на комплексной плоскости. Для функции действительной переменной метод Ньютона часто называют методом касательных. Поясним суть этого метода.

Пусть нам задана функция , для которой известно приближенное значение ее корня , а также значение функции в этой точке и значение её первой производной . Тогда, проводя касательную к графику функции в этой точке и определяя ее пересечение с осью , мы получим уточненное положение корня .

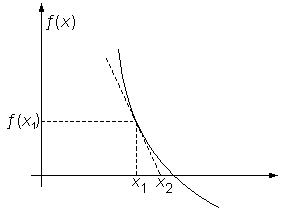
Т. к. уравнение касательной к в точке выглядит следующим образом:

то, приравнивая нулю, получаем, что уточненное значение корня связано с предыдущим значением соотношением

Беря теперь значение в качестве приближенного и повторяя эту процедуру, находим следующее приближение корня и т. д. При некоторых условиях эта последовательность сходится к корню уравнения .

Рассмотрим теперь комплексный случай. Рассмотрим уравнение и последовательность

Пусть . Как известно, это уравнение имеет три корня , , . При выборе различных процесс будет сходится к различным корням. Обозначим эти области притяжения через . Артур Кэли поставил задачу описания областей . Оказывается границы этих областей имеют фрактальную структуру.

program N3;

uses Graph, Crt;

type

Complex = Record

x : Real;

y : Real;

end;

const

iter = 50;

max = 1e+6;

min = 1e-6;

var

z, t, d : Complex;

p : Real;

x, y, n : Integer;

Cancel : Boolean;

gd, gm : Integer;

mx, my : Integer;

begin

Cancel := False;

Randomize;

gd := Detect;

InitGraph(gd,gm,'c:\bp\bgi');

Mx := GetMaxX div 2;

My := GetMaxY div 2;

for y := -my to my do

for x := -mx to mx do

begin

n := 0;

z.x := X * 0.005;

z.y := Y * 0.005;

d := z;

while (sqr(z.x)+sqr(z.y) < max) and (sqr(d.x)+sqr(d.y) > min)

and (n < iter) do

begin

t := z;

{z^3 - 1}

p := sqr(sqr(t.x)+sqr(t.y));

z.x := 2/3*t.x + (sqr(t.x)-sqr(t.y))/(3*p);

z.y := 2/3*t.y*(1-t.x/p);{}

d.x := abs(t.x - z.x);

d.y := abs(t.y - z.y);

Inc(n);

if keypressed then

Cancel := true;

end;

PutPixel(mx + x,my + y,16 - (n mod 16));

if cancel then exit;

end;

Readkey;

CloseGraph;

end.

Существуют и другие примеры алгебраических фракталов, например, биоморфы, дерево Барнсли, лямбда-фрактал (вариант множеств Мандельброта и Жюлиа), горящий корабль, паук.