2. Треугольник Серпинского

Для его построения из центра треугольника мысленно вырежем кусок треугольной формы, который своими вершинами будет упираться в середины сторон исходного треугольника. Повторим эту же процедуру для трех образовавшихся треугольников (за исключением центрального) и так до бесконечности. Если мы теперь возьмем любой из образовавшихся треугольников и увеличим его - получим точную копию целого. В данном случае мы имеем дело с полным самоподобием.

Построение треугольника Серпинского с помощью рекурсии

В 1915 году польский математик Вацлав Серпинский придумал занимательный объект, известный как решето Серпинского. Этот треугольник один из самых ранних известных примеров фракталов. Существует несколько способов построения этого фрактала. Один из них представляет следующий процесс. Берётся сплошной равносторонний треугольник, на первом шаге из центра удаляется перевёрнутый треугольник. На втором шаге удаляется три перевёрнутых треугольника из трёх оставшихся треугольников. Продолжая этот процесс, на -ом шаге удаляем перевёрнутых треугольников из центров оставшихся треугольников. Конца этому процессу не будет, и в треугольнике не останется живого места, но и на части он не распадётся - получится объект состоящий из одних только дырок. Это и есть треугольник Серпинского. Треугольник Серпинского также называют салфеткой Серпинского.

program FracSierp2;

uses CRT, Graph;

var

gd, gm : Integer;

const

iter = 5;

procedure tr(x1, y1, x2, y2, x3, y3: Real);

begin

Line(Round(x1), Round(y1), Round(x2), Round(y2));

Line(Round(x2), Round(y2), Round(x3), Round(y3));

Line(Round(x3), Round(y3), Round(x1), Round(y1));

end;

procedure draw(x1, y1, x2, y2, x3, y3: Real; n: Integer);

var

x1n, y1n, x2n, y2n, x3n, y3n : Real;

begin

if n > 0 then

begin

x1n := (x1 + x2) / 2;

y1n := (y1 + y2) / 2;

x2n := (x2 + x3) / 2;

y2n := (y2 + y3) / 2;

x3n := (x3 + x1) / 2;

y3n := (y3 + y1) / 2;

tr(x1n, y1n, x2n, y2n, x3n, y3n);

draw(x1, y1, x1n, y1n, x3n, y3n, n - 1);

draw(x2, y2, x1n, y1n, x2n, y2n, n - 1);

draw(x3, y3, x2n, y2n, x3n, y3n, n - 1);

end;

end;

begin

gd := Detect;

InitGraph(gd, gm, '');

tr(320,10,600,470,40,470);

draw(320,10,600,470,40,470,iter);{}

ReadKey;

CloseGraph;

end.

IFS-алгоритм построения

Треугольник Серпинского также легко можно построить с помощью трех IFS-преобразований. Эти преобразования имеют вид:

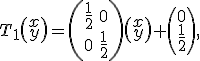
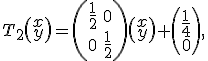
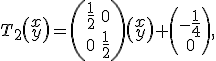
3. Драконова ломаная

Драконова ломаная относится к классу самоподобных рекурсивно порождаемых геометрических структур. Ломаная нулевого порядка представляет собой просто прямой угол. Изображение фигуры каждого следующего порядка строится путем рекурсивных замен каждого из отрезков фигуры младшего порядка на два отрезка, сложенных также в виде прямого угла.

Проделаем следующее: сложим полоску бумаги поперёк вдвое. Повторим это пару раз. После развертывания получим полоску, состоящую из восьми кусков. Посмотрев на эту полоску в профиль, мы увидим ломаную линию. Этот эксперимент можно продолжать и дальше, но не очень долго, из-за конечной толщины бумаги.

Предположим, что угол в каждом сгибе один и тот же. Обозначим этот угол через . Заметим, что на каждой вкладке мы поварачиваем либо влево либо вправо. Поэтому введём параметр , который принимает значение 1 когда мы поварачиваем влево и -1, когда вправо. Имеем:

Тогда

Следовательно, имеет следующие правила:

Следуя этому правилу, мы можем нарисовать ломанную линию, которая получается в результате сгибания полоски бумаги любое число раз.

На рисунке ниже приведена ломаная с .

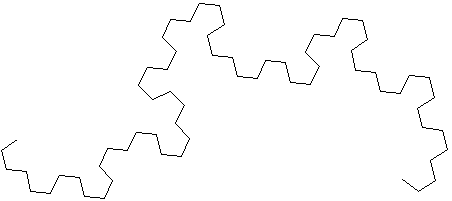
А если положить , то получим дракон Хартера-Хейтуэя.

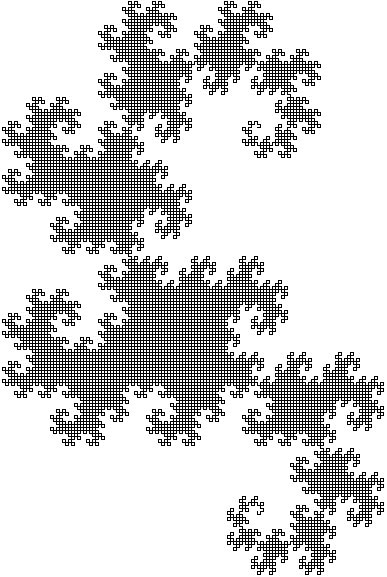
Можно также немного закруглять углы.

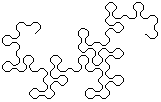
program Dragon;

uses Graph, Crt;

const

c = 1024*16;

d = 3;

da =pi/2;

var

i : Integer;

gd, gm : Integer;

a, x, y : Real;

procedure Lineto1(x, y, l, u : Real);

begin

Line(Round(x), Round(y), Round(x + l*cos(u)),

Round(y - l*sin(u)));

end;

function Opra(n : Integer) : Integer;

label

nach;

var

j : Integer;

begin

j := n;

nach:

if (j - 1) mod 4 = 0 then

Opra := -1

else if (j-3) mod 4 = 0

then Opra := 1

else

begin

j:=j div 2;

goto nach;

end;

end;

begin

gd := Detect;

InitGraph(gd,gm,'e:\bp\bgi');

x := 150;

y := 150;

a := pi/2;

for i := 1 to c + 1 do

begin

Lineto1(x,y,d,a);

x := x + d*cos(a);

y := y - d*sin(a);

a := a - da*Opra(i);

end;

ReadKey;

CloseGraph;

end.