
- •Розділ 1. Лінійне програмування
- •§ 1.1. Приклади задач лінійного програмування
- •§ 1.2. Загальна задача лінійного програмування. Основні означення. Стандартна задача. Канонічна задача
- •§ 1.3. Опукла множина. Опуклість множини базисних (опорних) планів злп. Геометрична інтерпретація злп
- •§ 1.4. Основні властивості злп. Симплексні перетворення
- •§ 1.5. Алгоритм симплексного методу. Таблична реалізація. Приклад
- •§ 1.6. Побудова початкового базисного (опорного) плану сзлп
- •§ 1.7. Двоїстість у лінійному програмуванні
- •, Якщо .
- •§ 1.8. Двоїстий симплексний метод (дсм)
- •Контрольні запитання та завдання
§ 1.2. Загальна задача лінійного програмування. Основні означення. Стандартна задача. Канонічна задача
Загальна задача лінійного програмування (в подальшому – ЗЛП) формально може бути описана так.
Визначити
вектор
![]() ,
який надає найбільшого чи найменшого
значення функції
,
який надає найбільшого чи найменшого
значення функції
![]() , (1.2.1)
, (1.2.1)
і при цьому задовольняє умови:
![]() ,
, ![]() ,
,
![]() (1.2.2)
(1.2.2)
![]() ,
,
![]() .
(1.2.3)
.
(1.2.3)
Тут
![]() ,
,
![]() ,
,
![]() – дійсні числа, знак
– дійсні числа, знак
![]() означає, в залежності від
означає, в залежності від
![]() ,
один зі знаків “=”, “
,
один зі знаків “=”, “![]() ” чи “
” чи “![]() ”.
”.
Лінійна
функція
![]() називається цільовою
функцією задачі.
називається цільовою
функцією задачі.
Якщо в
точці
![]() функція
функція
![]() досягає найбільшого значення, то функція
досягає найбільшого значення, то функція
![]() досягає в цій точці найменшого значення.
У зв’язку з цим домовимося про те, що в
подальшому будемо вести мову про
відшукання точки, в якій цільова функція
набуває найменшого значення. Якщо ж
буде ставитися задача про відшукання
точки, в якій цільова функція набуває
найбільшого значення, то, помінявши
знак цільової функції, ми перейдемо до
задачі про відшукання найменшого
значення нової цільової функції.
досягає в цій точці найменшого значення.
У зв’язку з цим домовимося про те, що в
подальшому будемо вести мову про
відшукання точки, в якій цільова функція
набуває найменшого значення. Якщо ж
буде ставитися задача про відшукання
точки, в якій цільова функція набуває
найбільшого значення, то, помінявши
знак цільової функції, ми перейдемо до
задачі про відшукання найменшого
значення нової цільової функції.
Ті з
відношень (1.2.3), в яких
![]() означає знак “
означає знак “![]() ”,
можна помножити на
”,
можна помножити на
![]() ,
добившись у такий спосіб того, що у
(1.2.3) фігуруватимуть лише рівності і
нерівності вигляду “
,
добившись у такий спосіб того, що у
(1.2.3) фігуруватимуть лише рівності і
нерівності вигляду “![]() ”.
”.
Виписуючи спочатку рівності, а потім нерівності, сформульовану задачу лінійного програмування (1.2.1) – (1.2.3) можна записати у еквівалентному вигляді:
визначити
вектор
![]() ,
який надає найменшого значення функції
,
який надає найменшого значення функції
![]() (1.2.4)
(1.2.4)
і при цьому задовольняє умови:
![]() ,
, ![]() ,
,
![]() (1.2.5)
(1.2.5)
 (1.2.6)
(1.2.6)
Звертаємо
увагу на те, що, згідно з (1.2.2) чи (1.2.5), не
обов’язково всі координати вектора
![]() невід’ємні. Ми сформували цей вектор
так, що перших
невід’ємні. Ми сформували цей вектор
так, що перших
![]() координат невід’ємні, а
координат невід’ємні, а
![]() можуть бути і від’ємними. Цього завжди
можна досягнути, ввівши необхідний
порядок нумерації змінних.
можуть бути і від’ємними. Цього завжди
можна досягнути, ввівши необхідний
порядок нумерації змінних.
Як
відомо, всяке дійсне число можна подати
у вигляді різниці двох невід’ємних
чисел. Тому у випадку
![]() змінну
змінну
![]() ,
,
![]() ,
можна подати у вигляді
,
можна подати у вигляді
![]() , (1.2.7)
, (1.2.7)
де
![]() та
та
![]() .
.
Замінивши
в (1.2.4) та (1.2.6) всі
![]() згідно з (1.2.7), отримаємо задачу лінійного
програмування, в якій усі змінні
невід’ємні. Нерівності типу “
згідно з (1.2.7), отримаємо задачу лінійного
програмування, в якій усі змінні
невід’ємні. Нерівності типу “![]() ”,
які входять до (1.2.6), можна перетворити
в рівності, додавши до їх лівих частин
так звані збалансовуючі
невід’ємні змінні
”,
які входять до (1.2.6), можна перетворити
в рівності, додавши до їх лівих частин
так звані збалансовуючі
невід’ємні змінні
![]() .
Зразу ж зауважимо, що ці змінні не
увійдуть у цільову функцію задачі.
.
Зразу ж зауважимо, що ці змінні не
увійдуть у цільову функцію задачі.
Отримана нова задача лінійного програмування характерна тим, що всі змінні, які беруть у ній участь, задовольняють умову невід’ємності, а обмеження вигляду (1.2.6) складаються лише з обмежень-рівностей. Задачу лінійного програмування такого типу в подальшому називатимемо стандартною задачею лінійного програмування (СЗЛП).
Зазначимо,
що в ЗЗЛП (1.2.1) – (1.2.3) і, відповідно, в
(1.2.4)-(1.2.6) беруть участь
![]() змінних
змінних
![]() ,
а у відповідній отриманій СЗЛП, згідно
з описаними вище правилами її побудови,
задіяні
,
а у відповідній отриманій СЗЛП, згідно
з описаними вище правилами її побудови,
задіяні
![]() змінних
змінних
![]()
![]() .
Число
.
Число
![]() може бути набагато більшим від
може бути набагато більшим від ![]() .
Наприклад, якщо
.
Наприклад, якщо
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
то
,
то
![]() .
Це збільшення розмірності задачі є
платою за стандартизацію. Стандартизація
ж дасть можливість порівняно просто
досліджувати властивості задачі,
формулювати і доводити необхідні
твердження, спільні для різних задач.
.
Це збільшення розмірності задачі є
платою за стандартизацію. Стандартизація
ж дасть можливість порівняно просто
досліджувати властивості задачі,
формулювати і доводити необхідні
твердження, спільні для різних задач.
Якщо
знайдено розв’язок відповідної СЗЛП,
то розв’язок початкової ЗЗЛП легко
знаходять, відкинувши
![]() і обчисливши
і обчисливши
![]() за формулами (1.2.7).
за формулами (1.2.7).
Для ілюстрації описаних вище правил переходу від ЗЗЛП до відповідної СЗЛП розглянемо приклад.
Нехай
необхідно визначити вектор
![]() ,
який надає найбільшого значення цільовій
функції
,
який надає найбільшого значення цільовій
функції
![]() (1.2.8)
(1.2.8)
і задовольняє умови
![]() ,
, ![]() (1.2.9)
(1.2.9)
та умови
 (1.2.10)
(1.2.10)
У цій
ЗЗЛП
![]() ,
,
![]() ,
умова невід’ємності не накладається
на
,
умова невід’ємності не накладається
на
![]() і на
і на
![]() .
Визначення найбільшого значення функції
.
Визначення найбільшого значення функції
![]() замінимо задачею визначення найменшого
значення функції
замінимо задачею визначення найменшого
значення функції
![]() .
.
Нерівність
![]() замінимо на рівносильну їй нерівність
замінимо на рівносильну їй нерівність
![]() ,
а змінні
,
а змінні
![]() та
та
![]() замінимо за правилом (1.2.7)
замінимо за правилом (1.2.7)
![]() ,
, ![]() ,
,
де
![]() – невід’ємні.
– невід’ємні.
Отримуємо нову задачу, яка полягає в знаходженні точки мінімуму функції
![]()
за умов
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
і

Залишилось
зробити останній крок, додавши до лівих
частин останніх нерівностей невід’ємні
збалансовуючі змінні
![]() та
та
![]() .
.
У результаті маємо відповідну СЗЛП:
визначити точку мінімуму функції
![]()
при виконанні умов
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
і умов-рівностей

Беручи до уваги викладені правила зведення ЗЗЛП до СЗЛП, ми можемо вважати, що ЗЛП записана уже у вигляді стандартної:
знайти точку мінімуму функції
![]() , (1.2.11)
, (1.2.11)
за умов
![]() ,
, ![]() , (1.2.12)
, (1.2.12)
і
![]() ,
, ![]() . (1.2.13)
. (1.2.13)
Особливо
підкреслимо: як правило,
![]() ,
бо у випадку
,
бо у випадку
![]() і відсутності серед рівнянь (1.2.13) лінійно
залежних розв’язку системи (1.2.13) може
не існувати або він може виявитися
єдиним і задача вибору вектора
і відсутності серед рівнянь (1.2.13) лінійно
залежних розв’язку системи (1.2.13) може
не існувати або він може виявитися
єдиним і задача вибору вектора
![]() зникає.
зникає.
Якщо
ввести в розгляд
![]() -вимірні
вектори-стовці
-вимірні
вектори-стовці
![]() ,
,
![]() ,
,
![]() -вимірні
вектори-стовці
-вимірні
вектори-стовці
![]() і нуль-вектор
і нуль-вектор
![]() та
та
![]() -матрицю
-матрицю
 ,
,
скалярний
добуток
![]() векторів
векторів
![]() та
та
![]() ,
то СЗЛП можна записати у вигляді.
,
то СЗЛП можна записати у вигляді.
Визначити
вектор
![]() ,
який надає найменшого (мінімального)
значення функції
,
який надає найменшого (мінімального)
значення функції
![]() (1.2.14)
(1.2.14)
і який задовольняє умови
![]() , (1.2.15)
, (1.2.15)
![]() . (1.2.16)
. (1.2.16)
У цьому випадку кажуть, що СЗЛП задана в матрично-векторній формі.
Іноді формально СЗЛП записують так
![]() ,
(1.2.17)
,
(1.2.17)
![]() . (1.2.18)
. (1.2.18)
Тут
![]() – множина векторів
– множина векторів
![]() ,
які задовольняють виписані у фігурних
дужках умови (1.2.15) і (1.2.16).
,
які задовольняють виписані у фігурних
дужках умови (1.2.15) і (1.2.16).
У подальшому ми будемо використовувати в основному таку форму запису СЗЛП:
![]() , (1.2.19)
, (1.2.19)
![]() , (1.2.20)
, (1.2.20)
![]() . (1.2.21)
. (1.2.21)
У задачі, як зрозуміло із форми запису, мова буде йти про визначення точки мінімуму цільової функції (1.2.19) при виконанні прямих обмежень (1.2.20) та непрямих обмежень (1.2.21), записаних у матрично-векторній формі.
Усякий
![]() -вимірний
вектор
-вимірний
вектор
![]() називається планом
задачі
(1.2.19) – (1.2.21).
Допустимим планом
цієї задачі називається такий
називається планом
задачі
(1.2.19) – (1.2.21).
Допустимим планом
цієї задачі називається такий
![]() -вимірний
вектор
-вимірний
вектор
![]() ,
який справджує (задовольняє) умови
(1.2.20) – (1.2.21).
,
який справджує (задовольняє) умови
(1.2.20) – (1.2.21).
Допустимий
план
![]() ,
на якому цільова функція
,
на якому цільова функція
![]() досягає мінімального значення
досягає мінімального значення
![]()
називається
оптимальним
планом
задачі
(1.2.19) – (1.2.21). Пара
![]() називається розв’язком
задачі
(1.2.19) – (1.2.21).
називається розв’язком
задачі
(1.2.19) – (1.2.21).
Якщо
ввести в розгляд стовпці матриці
![]()
 ,
,
 ,
...,
,
...,
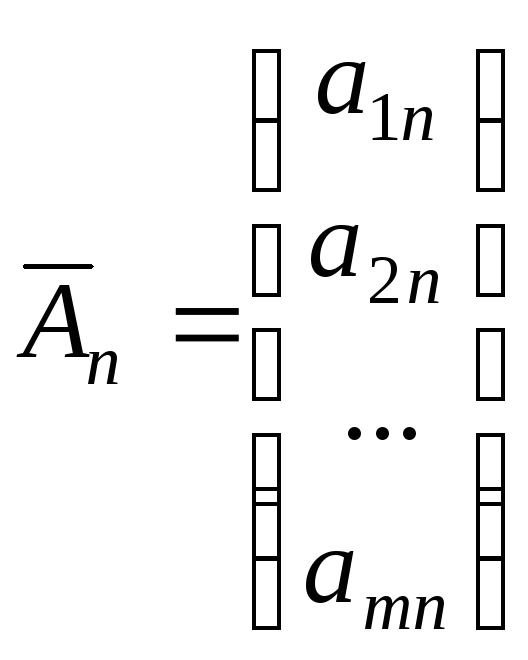 ,
,
то обмеження (1.2.21) можна записати у вигляді
![]() . (1.2.22)
. (1.2.22)
Отже,
кожній із компонент плану ставиться у
відповідність стовпчик матриці
![]() з тим же номером, що і у компоненти.
з тим же номером, що і у компоненти.
Згідно із прямими умовами (1.2.20), серед компонент допустимого плану можуть бути і такі, що дорівнюють нулеві.
Допустимий
план СЗЛП (1.2.19 – 1.2.21) називають базисним
планом
цієї задачі (часто – опорним
планом
задачі), якщо вектори
![]() ,
які мають такі ж номери, що й відмінні
від нуля компоненти плану
,
які мають такі ж номери, що й відмінні
від нуля компоненти плану
![]() ,
є лінійно незалежними.
,
є лінійно незалежними.
З курсу
лінійної алгебри відомо, що серед
![]() -вимірних
векторів
-вимірних
векторів
![]() лінійно незалежних є не більше ніж
лінійно незалежних є не більше ніж
![]() .
Це означає, що базисний (опорний) план
задачі (1.2.19) – (1.2.21) містить не більше
ніж
.
Це означає, що базисний (опорний) план
задачі (1.2.19) – (1.2.21) містить не більше
ніж
![]() компонент, які не дорівнюють нулю
(більших від нуля, згідно з (1.2.20)).
компонент, які не дорівнюють нулю
(більших від нуля, згідно з (1.2.20)).
Такий
базисний (опорний) план, який містить
рівно
![]() більших від нуля компонент
більших від нуля компонент
![]() ,
називають невиродженим
базисним (опорним) планом
задачі. Якщо ж цих компонент менше ніж
,
називають невиродженим
базисним (опорним) планом
задачі. Якщо ж цих компонент менше ніж
![]() ,
план називається виродженим.
,
план називається виродженим.
Для
зручності в подальших записах ми
вважатимемо, що відмінні від нуля
компоненти базисного плану є за нумерацією
першими. Якщо це не так, то легко здійснити
необхідну перенумерацію змінних. За
такої домовленості невироджений базисний
план задачі має вигляд
![]() .
.
При цьому матриця
 ,
,
називається
базисною
матрицею.
Зрозуміло, що
![]() ,
а також, що, взагалі кажучи, базисний
план задачі не обов’язково існує, або
не обов’язково єдиний.
,
а також, що, взагалі кажучи, базисний
план задачі не обов’язково існує, або
не обов’язково єдиний.
Змінні
![]() ,
які відповідають стовпцям
,
які відповідають стовпцям
![]() базисної матриці, називаються базисними
змінними.
Всі інші змінні називаються небазисними.
Набір векторів-стовпців базисної матриці
називається базисом
або базою
СЗЛП.
базисної матриці, називаються базисними
змінними.
Всі інші змінні називаються небазисними.
Набір векторів-стовпців базисної матриці
називається базисом
або базою
СЗЛП.
Проілюструємо сказане вище на простому прикладі СЗЛП.
Нехай задана задача
![]() ,
,
![]() ,
,
![]() ,
,

Тут
![]() ,
,
![]() .
.
Вектор
![]() є невиродженим базисним планом. Базисною
матрицею є матриця
є невиродженим базисним планом. Базисною
матрицею є матриця
![]() ,
(
,
(![]() ),
а базисними змінними –
),
а базисними змінними –
![]() та
та
![]() .
Невиродженим базисним планом є також
вектор
.
Невиродженим базисним планом є також
вектор
![]() .
У цьому випадку
.
У цьому випадку
![]() ,
(
,
(![]() ),
),
![]() та
та
![]() – базисні змінні, а
– базисні змінні, а
![]() – небазисні змінні.
– небазисні змінні.
Вектор
![]() є виродженим базисним планом, бо кількість
його ненульових компонент менша ніж 2.
є виродженим базисним планом, бо кількість
його ненульових компонент менша ніж 2.
Важливим
частковим випадком СЗЛП є випадок, коли
матриця
![]() цієї задачі містить
цієї задачі містить
![]() таких стовпців
таких стовпців
![]() ,
з яких можна сформувати одиничну матрицю
розмірності
,
з яких можна сформувати одиничну матрицю
розмірності
![]() ,
а праві частини обмежень-рівностей
невід’ємні. Стовпці
,
а праві частини обмежень-рівностей
невід’ємні. Стовпці
![]() можуть мати будь-які номери, але, не
порушуючи загальності в міркуваннях,
зручно вважати, що
можуть мати будь-які номери, але, не
порушуючи загальності в міркуваннях,
зручно вважати, що
![]() ,
,
![]() ,
...,
,
...,
![]() .
У стовпці
.
У стовпці
![]() одиниця
знаходиться на
одиниця
знаходиться на
![]() -му
місці. Таку СЗЛП називають канонічною.
-му
місці. Таку СЗЛП називають канонічною.
Отже, канонічною задачею лінійного програмування (КЗЛП) назвемо задачу
![]() , (1.2.23)
, (1.2.23)
![]() ,
, ![]() ; (1.2.24)
; (1.2.24)
 (1.2.25)
(1.2.25)
![]() ,
, ![]() . (1.2.26)
. (1.2.26)
У матрично-векторному вигляді задачу можна записати так:
![]() , (1.2.27)
, (1.2.27)
![]() , (1.2.28)
, (1.2.28)
![]() , (1.2.29)
, (1.2.29)
![]() . (1.2.30)
. (1.2.30)
Тут
 ,
, ![]() .
.
Якщо
відомо деякий базисний (опорний) план,
СЗЛП (1.2.19) – (1.2.21) з базисною матрицею
![]() ,
то відповідну КЗЛП легко отримати,
визначивши матрицю
,
то відповідну КЗЛП легко отримати,
визначивши матрицю
![]() та вектор
та вектор
![]() за формулами
за формулами
![]() ,
, ![]() . (1.2.31)
. (1.2.31)
Тут
![]() – обернена матриця до матриці
– обернена матриця до матриці
![]() .
.
Якщо
повернутись до розглянутого вище
прикладу, то базисному плану
![]() відповідає базисна матриця
відповідає базисна матриця
![]() .
.
![]() ,
,
![]() .
.
![]() .
.
Отже, відповідна КЗЛП має вигляд
![]() ,
,
![]() ,
,
![]() ,
,

Якщо
використати базисний план
![]() ,
то отримаємо іншу форму КЗЛП.
Обмеження-рівності матимуть вигляд
,
то отримаємо іншу форму КЗЛП.
Обмеження-рівності матимуть вигляд

Якщо не існує базисного (опорного) плану СЗЛП, то не існує і відповідної КЗЛП.
Якщо
задана КЗЛП (1.2.23) – (1.2.26), то, як легко
зрозуміти, базисним (опорним) планом
задачі є план
![]() .
.
Роль канонічної форми ЗЛП при визначенні розв’язку дуже важлива, що ми з’ясуємо при вивченні відповідного алгоритму.
Із
матриці
![]() стандартної задачі можна виділити
стандартної задачі можна виділити
![]()
матриць
розміром
![]() .
.
При
![]() і
і
![]() це число рівне 252.
це число рівне 252.
Перевірка виділеної матриці на базисність пов’язана зі знаходженням оберненої матриці. Таких перевірок може бути багато, що вимагає великої кількості операцій.
Пізніше ми познайомимося з деякими регулярними методами визначення хоча б одного базисного плану (якщо такі плани існують) та побудови відповідної КЗЛП.
