, Якщо .

Для симетричної пари двоїстих задач останнє Твердження легко формулюється у вигляді

Твердження 1.7.5. Допустимі базисні плани та є розв’язками задач (1.7.12) – (1.7.14) та (1.7.15) – (1.7.17), відповідно, тоді і тільки тоді, коли

для всіх

та

для всіх .

Зауваження. Неважко довести, що у випадку, коли вектор є оптимальним базисним планом СЗЛП, а – відповідна базисна матриця, то є розв’язком відповідної двоїстої задачі. Тут – вектор коефіцієнтів цільової функції при базисних змінних, – транспонована обернена базисна матриця.

Отже, за відомим розв’язком СЗЛП можна побудувати розв’язок відповідної двоїстої задачі.

Твердження 1.7.4 і 1.7.5 можуть бути використані для перевірки оптимальності заданого допустимого плану СЗЛП.

Легко перевірити, що вектор є базисним допустимим планом задачі

,

, , , ,

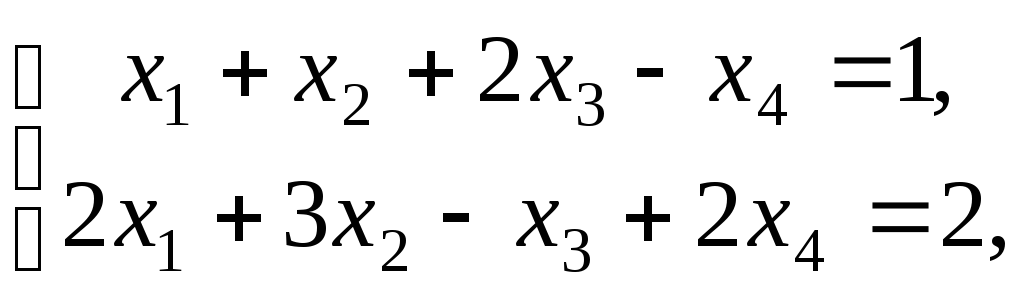
Двоїстою до виписаної задачі є задача

,

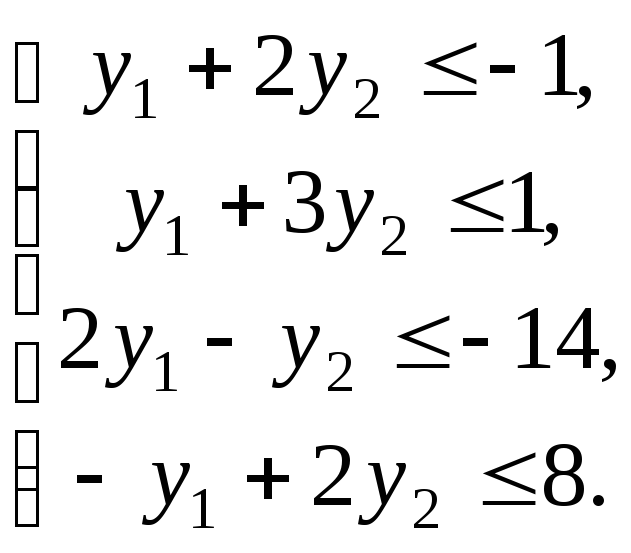
Маємо , , .

Згідно із Твердженням 1.7.4, вектор є розв’язком вихідної задачі, якщо існує розв’язок системи рівнянь

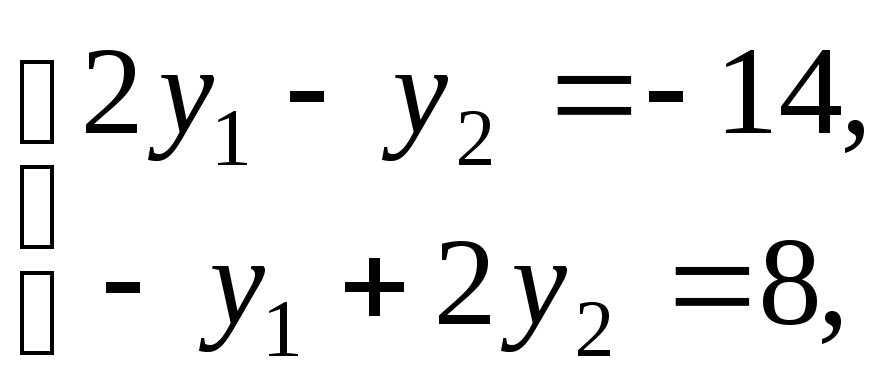
який задовольняє систему нерівностей

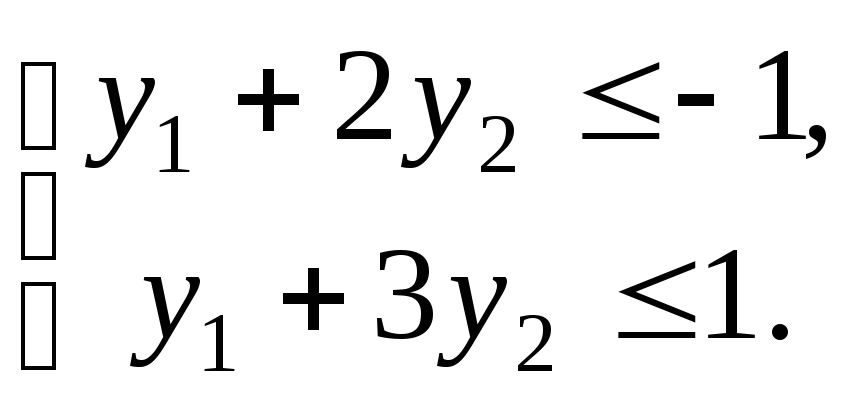
Розв’язавши систему рівнянь, отримуємо ; .

Легко переконатися, що система нерівностей теж виконується:

Отже, вектор – розв’язок вихідної задачі.

Вектор теж є базисним допустимим планом вихідної задачі. Тут , , . Для того, щоб цей вектор був розв’язком вихідної задачі, необхідно і досить, щоб існував розв’язок системи рівнянь

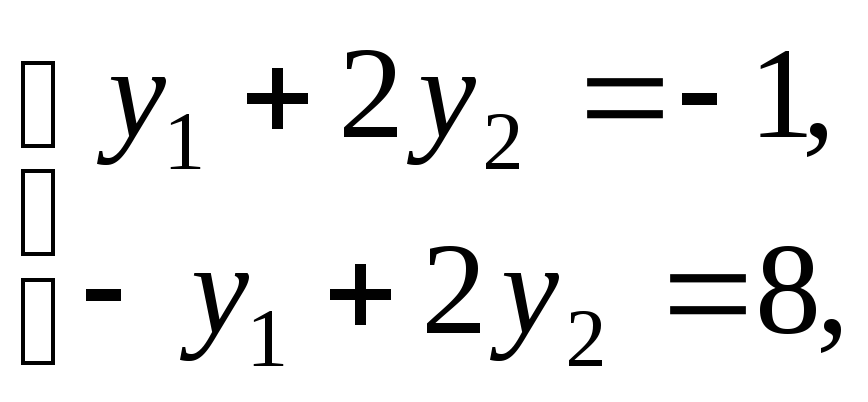
який задовольняє систему нерівностей

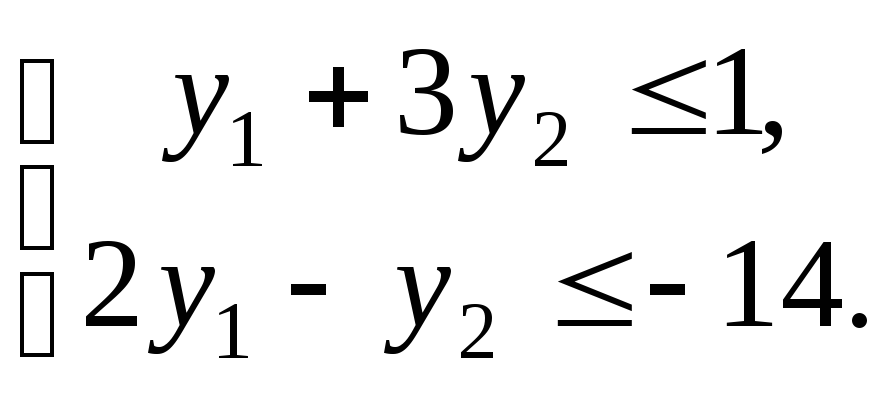
Розв’язавши систему рівнянь, маємо

; .

Це єдиний розв’язок системи. Знайдені значення та не задовольняють систему нерівностей, бо , а .

Отже, вектор не є розв’язком вихідної задачі.

Зрозуміло, що розв’язок задачі (1.7.1) – (1.7.3) залежить від значень . Отже, і є деякою функцією параметрів задачі , які визначають об’єми ресурсів, наявних для реалізації плану.

Але, згідно із Твердженням 1.7.3,

,

де компоненти відповідної двоїстої задачі (1.7.4) – (1.7.5).

Отже,

.

Останнє дає можливість інтерпретувати компоненти розв’язку двоїстої задачі як миттєві швидкості зміни затрат при зміні відповідного ресурсу.

Ми приходимо до висновку, що змінні двоїстої задачі є оцінками потенційної можливості зменшення чи збільшення затрат за рахунок збільшення відповідного ресурсу в умовах оптимального функціонуючого об’єкта, модель якого описується задачею лінійного програмування.

Розглядаючи пару взаємно двоїстих задач, можна аналізувати також вплив на розв’язок задачі варіації коефіцієнтів цільової функції.

Взагалі кажучи, з точки зору економічного трактування, задачі дослідження впливу варіації параметрів та на оптимальне значення цільової функції (задача параметричної стійкості) можуть трактуватися як задачі знаходження меж коливання цін на продукцію і меж коливання об’ємів наявних ресурсів, при яких прийнятий план випуску продукції залишається оптимальним.

§ 1.8. Двоїстий симплексний метод (дсм)

Викладені у попередньому параграфі положення, пов’язані з поняттям двоїстості, дають можливість розробити ще один метод розв’язання ЗЛП. При цьому відповідний алгоритм дозволяє розв’язувати одночасно кожну з пар двоїстих задач.

Нехай задана СЗЛП

, (1.8.1)

, (1.8.2)

. (1.8.3)

Як і раніше, вважаємо, що ранг матриці дорівнює . Отже, існує лінійно незалежних стовпців цієї матриці. Матриця , складена із цих стовпців, невироджена. Помноживши (1.8.2) зліва на , матимемо

.

Тут матриця містить стовпчики, які утворюють одиничну матрицю. Ми без порушення загальності можемо вважати, що ці стовпці є першими (відповідають змінним ).

Замість задачі (1.8.1) – (1.8.3) отримуємо еквівалентну їй задачу

,

,

.

Або в координатній формі

, (1.8.4)

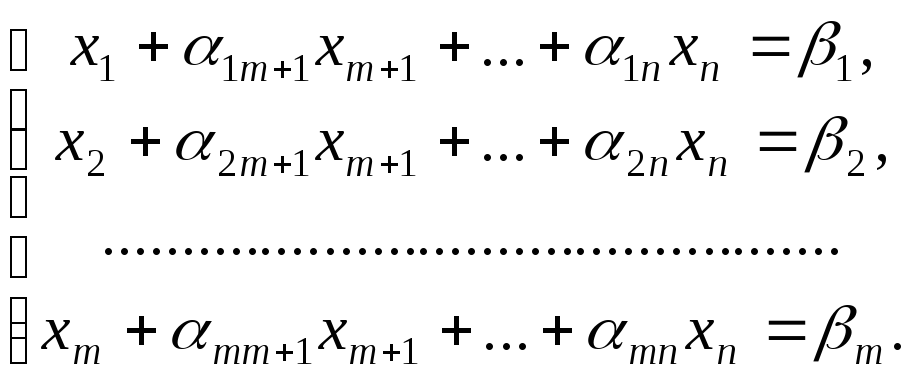(1.8.5)

, , ..., . (1.8.6)

Виписана задача за формою запису подібна до КЗЛП, відповідну задачі (1.8.1) – (1.8.3), але такою може не бути, бо на не накладаються умови невід’ємності. Зате в подальшому ми на задачу (1.8.1) – (1.8.3) накладатимемо додаткову вимогу

, , ..., , (1.8.7)

де – відносна оцінка змінної .

Задача (1.8.4) – (1.8.7) називається майже канонічною задачею лінійного програмування (МКЗЛП), відповідною задачі (1.8.1) – (1.8.3). Зрозуміло, що, як тільки ця задача стає канонічною, тобто , , ..., , то вектор є оптимальним планом задачі (1.8.1) – (1.8.3).

Якщо із (1.8.5) виразити базисні змінні через небазисні і відповідні вирази підставити у цільову функцію, то отримуємо

і від (1.8.4) – (1.8.7) можна перейти до еквівалентної МКЗЛП

,

, ,

, ,

, .

Відповідна двоїста задача може бути записана у вигляді

, (1.8.8)

, , (1.8.9)

, . (1.8.10)

Ця задача введенням збалансовуючих змінних легко зводиться до канонічного вигляду і розв’язується симплексним методом, після чого за теоремами двоїстості можна знайти розв’язок (1.8.1) – (1.8.3). Відмітимо, що у взаємо двоїстих задачах (1.8.4) – (1.8.7) та (1.8.8) – (1.8.10) відносні оцінки та праві частини помінялись ролями.

Зазначені обставини і пояснюють зміст алгоритму двоїстого симплексного методу (ДСМ), до опису якого ми зараз перейдемо.

Результати обчислень зводять у таблиці, які майже не відрізняються від таблиць, пов’язаних із симплексним методом. Правда, у зв’язку з тим, що відносні оцінки і праві частини міняються ролями, в цих таблицях, порівняно із симплексним методом, міняються ролями рядки і стовпці.

Насамперед педкреслимо, що ДСМ застосовуються до майже канонічної задачі (1.8.4) – (1.8.7). Реалізація методу полягає у здійсненні послідовності кроків:

Крок 1. Звести задачі лінійного програмування до майже канонічного вигляду. Перейти до кроку 2.

Крок 2. Якщо , , ..., , то вектор є розв’язком задачі (1.8.1) – (1.8.3). Перейти до кроку 6. Якщо ж не всі невід’ємні, перейти до кроку 3.

Крок 3. Визначити такий номер , для якого

.

Якщо існує таке , що , то перейти до кроку 4. Якщо ж для всіх , , то розв’язку задачі не існує (цільова функція необмежена знизу, множина планів двоїстої задачі порожня). Процес розв’язування завершено.

Крок 4. Визначити номер , такий, що

.

Перейти до кроку 5.

Крок 5. Ввести в число базисних змінних змінну , вивести із числа базисних змінних змінну . Провідним елементом таблиці є елемент . Перерозрахунок таблиці здійснюється за тією ж схемою прямокутників, що і в симплексному методі. Перейти до кроку 2.

Крок 6. Виписати отриманий план задачі (1.8.1) – (1.8.3), підрахувати значення цільової функції . Оптимальний план двоїстої задачі можна визначити як вектор значень відносних оцінок, які розміщені у стовпцях таблиці, відповідних початковій базисній матриці, помінявши знак оцінок. Процес розв’язування завершено.

Питання про те, як задану ЗЛП звести до МКЗЛП, ми залишили відкритим. Зауважимо лише, що такі методи існують. Вони є аналогами методу штучної бази.

На завершення проілюструємо ДСМ на простому прикладі.

Розв’язати задачу лінійного програмування

,

, ,.

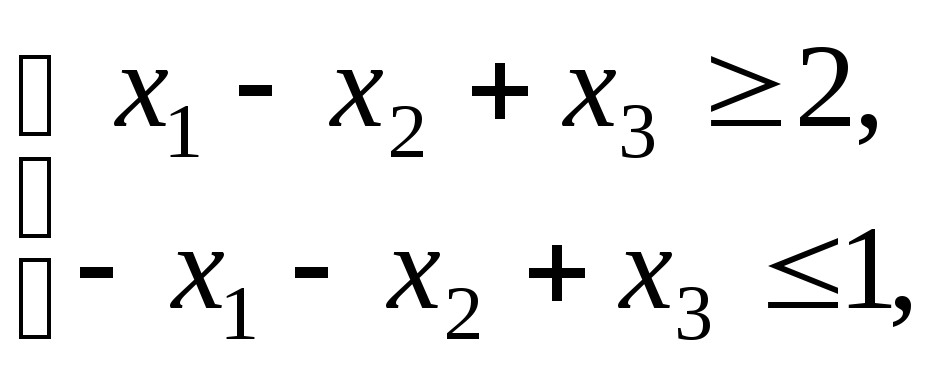
Щоб стандартизувати задачу, введемо збалансовуючі змінні , .

Маємо

,

, , , , .

Помноживши перше рівняння на , отримаємо задачу

,

, ,, , .

Тут

,

, .

Легко побачити, що , , , , і ми отримали майже канонічну задачу. Початковий базис відповідає змінним та .

Будуємо таблиці для двоїстого симплексного методу.

На третьому кроці бачимо, що . Отже, з числа базисних треба вивести змінну . Оскільки , то і треба ввести в число базисних.

Провідний елемент .

№ ітер.	баз.	баз.	1	1	2	0	0		Зауваження
1		0		1	–1	1	0	–2	вивести
		0	–1	–1	1	0	1	1	ввести
			1	1	2	0	0
			1		2
2		1	1	–1	1	–1	0	2
		0	0	–2	2	–1	1	3
			0	2	1	1	0		Процес завершено

Двоїстою до заданої задачі є задача

,

, .

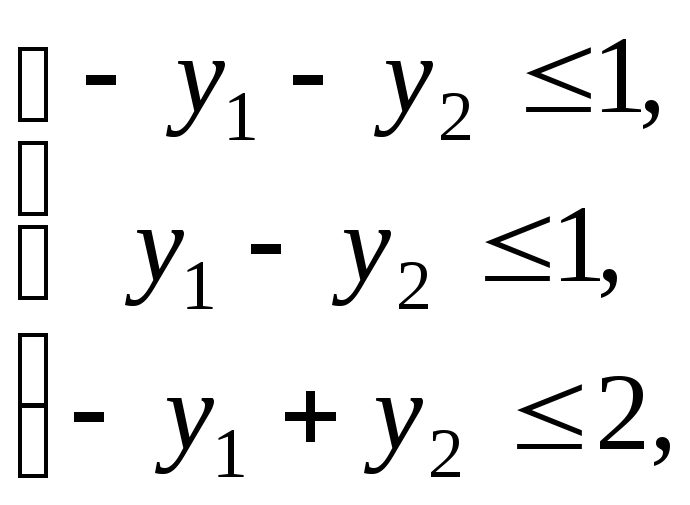
Із таблиці видно, що , .

Отже, .

Цей вектор можна визначити і згідно із зауваженням в § 1.7 за формулою

.

У нас

, .

Тому

, ,

.

Можна було б також використати Твердження 1.7.4 і визначити значення та із співвідношень

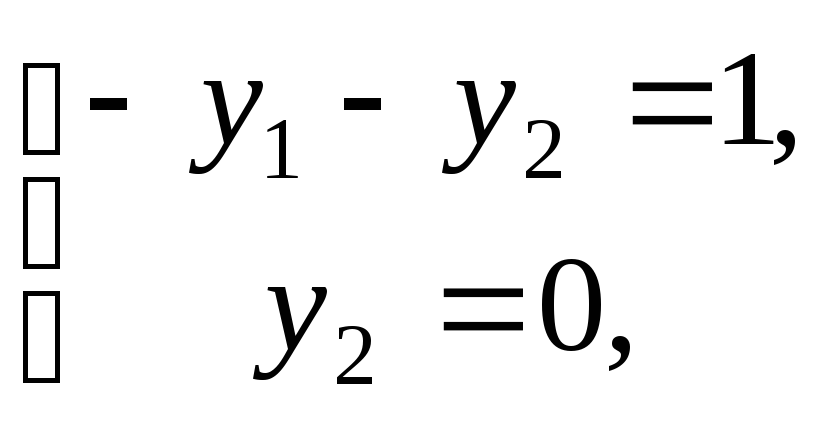
і

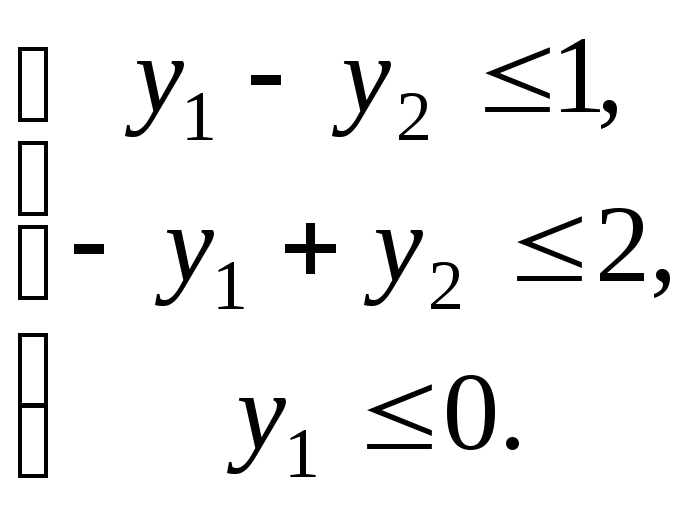
Маємо , і .

На цьому завершимо знайомство з методами розв’язання задач лінійного програмування, загальними властивостями таких задач. У наступних розділах ми ще зустрічатимемось із ЗЛП, будемо використовувати їх загальні властивості, але основну увагу ми приділимо специфіці отриманих математичних моделей і, відповідно, постараємося, з метою спрощення алгоритмів розв’язування, цю специфіку використовувати.