§ 1.3. Опукла множина. Опуклість множини базисних (опорних) планів злп. Геометрична інтерпретація злп

Множина точок -вимірного векторного простору називається опуклою, якщо з того, що дві точки та належать множині випливає, що всяка точка відрізка є точкою множини (весь відрізок міститься в ).

Приклади опуклих множин , , на площині зображено нижче.

Рис. 1.3.1

Множини , не є опуклими,

Рис. 1.3.2

бо існують точки відрізка , які не належать .

Порожню і одноточкову множини домовимося вважати опуклими.

Формально означення можна подати так:

множина точок -вимірного простору називається опуклою, якщо з того, що і , для будь-якого випливає

.

Всякій точці ставиться у відповідність її радіус-вектор . Якщо є множиною векторів, то вона називається опуклою, коли для будь-якого із та випливає, що . Остання форма означення використовуватиметься нами, коли мова йтиме про множину допустимих планів ЗЛП.

Зупинимось на кількох простих прикладах.

Множина точок , координати яких справджують рівняння виду

,

називається гіперплощиною в . У випадку ця множина є площиною.

Нехай точки і належать гіперплощині, тобто

і .

Перше рівняння помножимо на і додамо до другого, помноженого на . Матимемо

або

.

Це означає, що точка

належить гіперплощині при будь-якому .

Отже, гіперплощина є опуклою множиною.

Множина точок , координати яких справджують нерівності виду

або

,

називається півпростором у .

Аналогічно попередньому легко переконатися, що півпростір є опуклою множиною.

У ЗЗЛП присутні прямі обмеження-нерівності, а також непрямі обмеження у вигляді рівностей та нерівностей. Кожне з цих обмежень визначає півпростір чи гіперплощину, які, як ми з’ясували, є опуклими множинами. Допустимий план задачі повинен справджувати всі обмеження, тобто належати всім відповідним опуклим множинам (належати їх перетину).

Неважко переконатися, що перетин будь-якої кількості опуклих множин є опуклою множиною. Нехай, наприклад, дві множини та є опуклими, а множина – їх перетин. Якщо порожня або одноточкова, то, за домовленістю, вона опукла.

Нехай містить більше, ніж одну точку

, .

Оскільки є перетином та , точки і є точками і , і . Ці множини опуклі. Значить, точка належить і , і при будь-якому . Але спільні для і точки належать їх перетину . Тому є точкою . Отже, множина опукла.

Зі сказаного вище робимо висновок, що множина допустимих планів ЗЛП опукла.

Ця властивість множини допустимих планів дуже важлива властивість ЗЛП.

Так як ця множина визначається лінійними обмеженнями (межі утворюються гіперплощинами), то її часто називають многогранною множиною. У випадку, коли множина обмежена, її називають допустимим многогранником задачі.

Дамо ще одне потрібне в подальшому означення, пов’язане з поняттям опуклої множини і корисне при розв’язуванні задач лінійного програмування.

Точка опуклої множини називається вершиною цієї множини, якщо не існує таких різних точок , множини і такого , що

, , ..., .

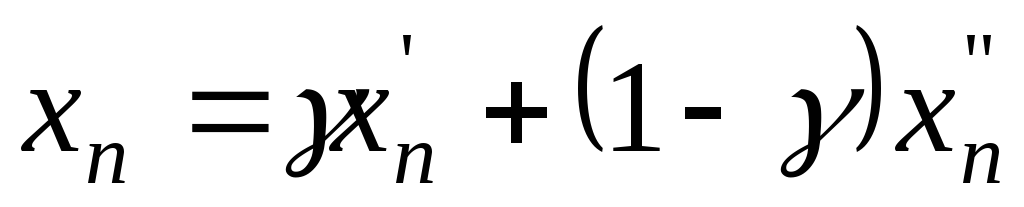Іншими словами – не існує таких точок та множини , що точка є точкою відрізка .

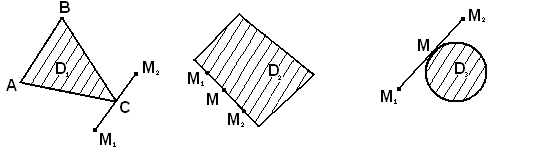
Рис. 1.3.3

Точки множини є її вершинами, точка множини не є вершиною, а всяка точка кола, яка обмежує круг , є вершиною цього круга.

У випадку ЗЛП можна легко розв’язати, зобразивши на площині множину допустимих планів.

Розглянемо приклад.

,

,

Побудуємо на площині прямі лінії

, , , , ,

які разом із прямою утворюють межу опуклої множини допустимих планів задачі.

Рис. 1.3.4

Ця множина допустимих планів – шестикутник із вершинами

, , , , , .

Як відомо з курсу вищої математики, цільова функція зростає в напрямку вектора і спадає в протилежному напрямку. Лініями рівня цієї функції є прямі , де – будь-яке дійсне число.

Зображаємо лінію рівня, яка проходить через точку допустимої множини (ми, наприклад, зобразили пряму , яка проходить через точку ).

Для визначення точки максимуму ми повинні переміщати побудовану пряму в напрямку вектора так, щоб вона залишалась перпендикулярною цьому вектору і переміщати доти, поки ця пряма проходитиме хоча б через одну точку допустимої множини. Визначена “крайня” точка і є точкою максимуму цільової функції. Для знаходження точки мінімуму пряму треба переміщати в напрямку, протилежному вектору .

У нашому випадку, як видно з рисунка, точкою максимуму є точка , а точкою мінімуму є точка . При цьому

, .

Розв’язком поставленої задачі є пара , де

, .

Запропонований метод розв’язування задачі називається графічним. Такий метод дозволяє не тільки розв’язувати прості ЗЛП, але і робити деякі висновки про можливі ситуації, про деякі властивості цих задач.

Наприклад, у випадку

Рис 1.3.5

мінімум цільової функції досягається в точці 0, а максимум – у будь-якій точці відрізка .

У випадку

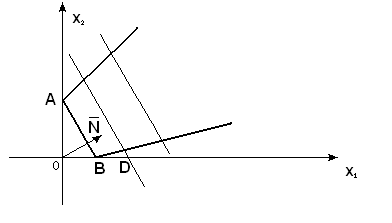
Рис. 1.3.6

мінімальне значення цільової функції досягається в будь-якій точці відрізка , а максимальне значення не досягається (пряму можна переміщати в напрямку скільки завгодно, цільова функція не обмежена зверху).

Міркування типу викладених вище називають геометричною інтерпретацією задач лінійного програмування.

Зауважимо, що геометрично можна розв’язувати і задачі з більшою кількістю змінних. Достатньою умовою для цього є, наприклад, умова , де – матриця системи обмежень-рівностей СЗЛП.

Розв’яжемо геометрично задачу

,

, , , ,

Тут , матриця системи обмежень рівностей

має ранг 2, бо і змінні та можна виразити через змінні , , розв’язавши систему

Одержимо

Згідно з умовами задачі , , , . Отже, одержуємо

Замінивши в цільовій функції та знайденими виразами, матимемо нову цільову функцію

.

Сталий доданок не впливає на точку максимуму, а впливає лише на значення цільової функції. Тому розв’яжемо задачу

,

, ,

Побудуємо відповідний рисунок

Рис. 1.3.7

Множиною допустимих планів є трикутник .

З рисунка видно, що максимальне значення цільової функції досягається в точці .

Координати цієї точки знаходимо розв’язавши систему

Одержуємо ; . Легко підрахувати, що

,

.

Маємо оптимальний план

.

При цьому

.

Наведена вище геометрична інтерпретація ЗЛП дозволяє зробити деякі попередні висновки про властивості цих задач.

Ми встановили, що множина допустимих планів є опуклою. Ця множина може бути порожньою, якщо обмеження суперечливі. Якщо ж вона містить хоча б два різних плани, то містить їх нескінченно багато. ЗЛП може не мати розв’язку у двох випадках – або множина допустимих планів порожня, або цільова функція необмежена (знизу чи зверху в залежності від формулювання задачі).

Важливий висновок, який стосується точок допустимої області, в яких досягається мінімум (максимум) цільової функції.

Якщо цільова функція ЗЛП досягає мінімуму (максимуму) на множині допустимих планів, а ця множина має вершини, то мінімум (максимум) цільової функції досягається хоча б у одній із вершин.

Більш детально на властивостях ЗЛП ми зупинимося в наступному параграфі.