Лекция 9-10. Системы массового обслуживания.

Физические и математические системы массового обслуживания. Структура СМО. Коэффициент загрузки СМО. Основные характеристики работы СМО с ограниченным числом состояний. Основная расчетная формула определения характеристики СМО с неограниченным числом состояний.

Физические системы массового обслуживания (СМО) встречаются во всех областях деятельности человека. Системами называются потому, что есть поступления называемых заявок на обслуживание и есть механизм, который выполняет заявки. Если интенсивность поступления заявок больше, чем их обслуживание возникает очередь. Простой в очереди может привести к потере клиентов, поступающих на обслуживание или привести к большим денежным затратам. Например, морские транспортные средства перевозящие различные грузы приходят в порт. Если причалы заняты другими морскими транспортными средствами, они остаются на рейде, ждут в очереди, пока поступить либо на погрузку на разгрузки. Если эти работы организованны не достаточно хорошо, то простой на рейдах длительный, что обходится очень дорого. Ставится вопрос, как необходимо организовать обслуживание судов, чтобы простой свести к минимуму.

Математический аппарат, который исследует процессы образования очередей или задержки в обслуживании также называется системами массового обслуживания (СМО). Практическое применение моделей СМО осуществляются в двух аспектах, это когда необходимо исследовать функционирующую систему и выявить причины недостаточной эффективности ее работы или на стадии создания системы, когда необходимо определить структуру системы, которая имела определенные показатели своей работы. Методы СМО хорошо работает, когда рассматриваемая система состоит из большого числа тождественных или сходных элементов.

СМО поддается количественному анализу. Однако на фоне реальных ситуаций выглядит весьма упрощенно. Хотя изучаются довольно простые системы, результаты изучения позволяют получить представление о качественном и приблизительно количественном поведении реальной системы.

Физическую СМО можно математически описать, задавая следующие компоненты:

• входной поток т.е. поток поступающих заявок на обслуживание;

• дисциплину очереди;

• механизм обслуживания.

Для определения входного потока требуется задать вероятностный закон, управляющий последовательностью моментов поступления заявок на обслуживание. Источник поступления заявок считается неисчерпаемым, т.е. считается, что заявка всегда поступит.

Дисциплина очереди описывает поведение заявки, поступившей на вход системы до непосредственного поступления на обслуживание.

Механизм обслуживания характеризуется продолжительностью процедуры обслуживания и количеством заявок, обслуживаемых одновременно. Продолжительность обслуживания зависит от структуры механизма обслуживания и может задаваться вероятностным законом или быть постоянной величиной. Для описания механизма обслуживания требуется указать количество приборов, составляющих механизм, и их расположение. Приборы могут располагаться параллельно или последовательно.

Характеристики, которые необходимо получить, исследуя СМО, зависит от реальных условий, однако часто интересует следующее:

• вероятность того, что в системе нет ни одной заявки;

• среднее число требований в очереди;

• среднее число требований в СМО;

• среднее время ожидания требований в очереди;

• коэффициент спроса требований в очереди и в системе обслуживания и др.

Способы определения этих характеристик зависит от математической модели СМО. Математическую модель порождает непосредственная конкретизация входного потока, дисциплины очереди и механизма обслуживания, каждый из которых может иметь различные представления в зависимости от того к какой сфере работ можно отнести СМО и как ее можно формализовать. На рис. 3,4,5 приведены характеристики всех составляющих математическую модель СМО.

Характеристики входного потока

по характеру поступления заявок

по количеству заявок

по периодичности заявок

стационарный входной поток

не стационарный входной поток

единичное поступление

спутниковое поступление

периодический входной поток

не периодичный входной поток

Рис. 3. Характеристики входного потока

Характеристики дисциплины очереди

по числу мест очереди

по времени пребывания в очереди

по порядку поступления на обслуживание

ограничена длина очереди

не ограничена длина очереди

ограничено время пребывания в очереди

не ограничено время пребывания в очереди

в порядке поступления

в обратном порядке

случайный выбор

Рис. 4. Характеристики дисциплины очереди

Характеристики механизма обслуживания

один прибор

несколько приборов

одно-фазовая одноканальная СМО

параллельное соединение

последовательное соединение

смешанное соединение

многоканальная СМО

многофазовая СМО

многофазовая многоканальная СМО

Рис. 5. Характеристики механизма обслуживания

Приведем пример конкретной СМО, на основе которой можно построить математическую модель, непосредственно описывая каждую из трех составляющих. Итак, одно-фазовая одноканальная система массового обслуживания с не периодичным стационарным входным потоком и ограниченным числом мест в очереди. Характеристика такова, заявки поступают на обслуживание по одной. Интервалы времени, через которые поступают заявки, зависит только от интенсивности и не зависит от никаких других факторов. Они имеют случайный характер и не повторяются. Механизм обслуживания состоит из одного прибора. В очереди может находиться не больше заранее заданного числа заявок. Построить математическую модель такой системы будет означать: задать вероятностный закон поступления заявок. Это будет закон Эрланга, с заданной интенсивностью .

Длительность обслуживания механизма обслуживания либо будет задано конкретным числом, либо вероятностным законом обслуживания, причем одного прибора. Число мест в очереди также будет представляться конкретным числом. Кроме основных характеристик СМО вводится еще одно называемое состоянием системы. Состояние системы определяется числом заявок одновременно находящихся в системе. Если длина очереди определена конкретным числом, то система считается с конечным числом состояний, а если очередь не ограничена, то с бесконечным числом состояний. От этого зависит метод определения основных характеристик системы.

Обозначим через  - интенсивность поступления заявок, а через  - интенсивность обслуживания. Коэффициент загрузки механизма обслуживания  вычисляется по разному для одноканальной - однофазовой системы

,

для многоканальной - однофазовой

;

где , s – число каналов

Пусть m- максимальное количество заявок в системе, k – текущее количество требований (0km).

Основные характеристика для s – канальной системы обслуживания со стационарным входным потоком и ограниченным числом заявок в очереди вычисляются по следующим формулам.

Вероятность того, что в системе находится k требований P_k определяется по-разному в зависимости одноканальная (s=1) или многоканальная СМО (s>1)

;

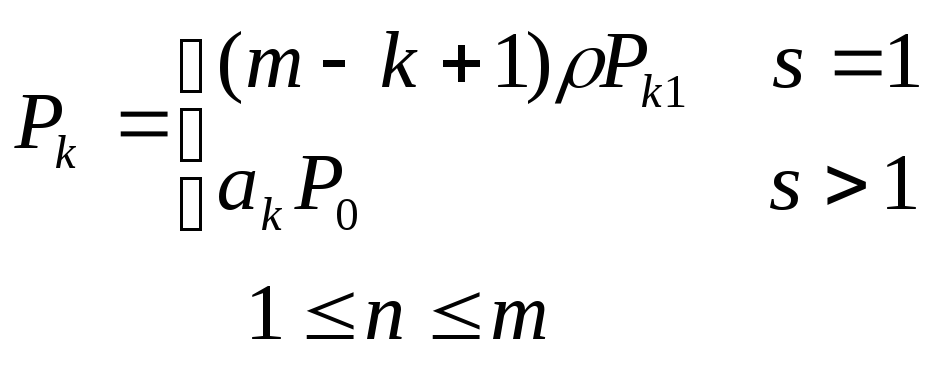где .

Вероятность того, что все s каналы свободны, т.е. простой каналов

При s=1

.

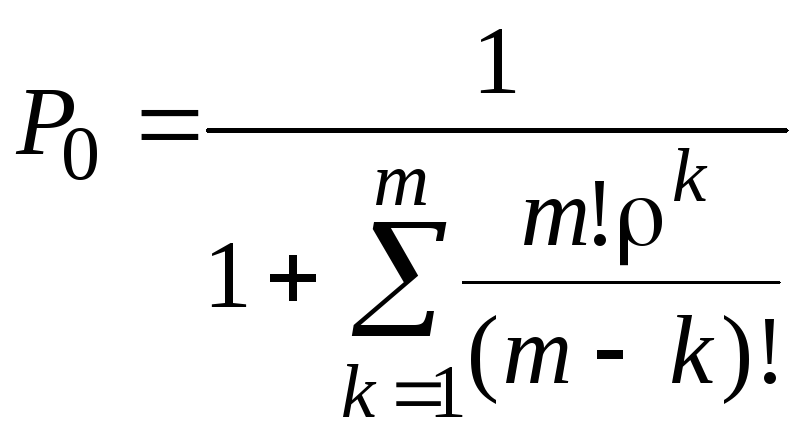При s>1

.

Математическое ожидание числа требований в очереди

.

Математическое ожидание числа требований СМО

.

Математическое ожидание простоя каналов обслуживания

.

Среднее время ожидания требований в очереди

.

Коэффициент простоя требований в очереди, %

.

Коэффициент простоя требований в очереди и на обслуживание

.

Коэффициент простоя каналов обслуживания

Приведем расчет основных характеристик s – канальной системы обслуживания со стационарным входным потоком и неограниченным числом заявок в очереди. Такие СМО характеризуются тем, что заявка, заставшая все каналы занятыми, становится в очередь и ожидает, пока один из каналов освободится. Как только канал освобождается, одна из заявок, стоящая в очереди, поступает на обслуживание. Такие системы являются наиболее распространенными. Основные расчетные формулы следующие.

Вероятность того, что все s каналы свободны, т.е. простой каналов

.

Вероятность того, что все каналы полностью заняты (k=s)

.

Вероятность того, что имеется очередь (k>s)

.

Среднее время ожидания заявки в очереди до начала обслуживания

.

- где t_обсл определяется исходя из интенсивности каналов.

Средняя длина очереди

.

Среднее число заявок, находится в системе

.

Среднее время пребывания в системе

.

Пример 1. В цехе предприятия функционируют 6 однотипных станков, которые обслуживает один механик. Станки выходят из строя. В обязанности механика входит устранение неисправности. Неисправности возникающие в станках, носят случайный характер и возникают с определенной интенсивностью. Никакие внешние воздействия не учитываются. В среднем, в течении одного числа из строя выходит одна машина. Продолжительность осмотра составляет в среднем 6 минут. Определить загруженность механика и процесс обслуживания станков.

Математическая модель такой системы следующая: механик интерпретируется как механизм обслуживания, станки с неисправностями составляют поток заявок. Интенсивность поступления заявок =1; Система одноканальная (s=1) со стационарным входным потоком. Интенсивность обслуживания =10. Число заявок в СМО ограниченное (в очереди не может быть больше пяти заявок).

Необходимо определить:

• коэффициент простоя механика ₁;

• коэффициент простоя станков в очереди ₂;

• коэффициент пребывания станков в СМО ₃;

• среднее время ожидания обслуживания t_ож.

Исходные данные следующие

Вероятности нахождения СМО в определенном состоянии

Р₁=(6-1+1)*0,1*0,4840=0,2900

Р₂=0,1450;

Р₃=0,0580;

Р₄=0,0170;

Р₅=0,0037;

Р₆=0,0003;

Поскольку система обязательно находится в одном из состояний, то . Можно проверить правильность счета.

Средняя длина очереди:

Среднее число требований в системе:

.

Среднее время ожидания механика для устранения неисправности:

.

Коэффициент простоя станка в очереди

.

Коэффициент простоя станка с учетом времени устранения неисправности:

.

Коэффициент простоя механика:

.

Потери рабочего времени механика весьма значительны и составляют почти половину времени (48%). Значит, механик может обслуживать значительно больше станков, чем шесть. Однако, это может привести к значительному увеличению коэффициентов ₂ и ₃. Зная потери, связанные с потерями станков и ожиданием механика, можно провести расчет и определить наиболее выгодный вариант по числу закрепляемых за механиком станков.

Пример 2. Комбинат бытового обслуживания принимает заказы на ремонт и перелицовку верхней одежды. В среднем в течении месяца поступает 10 заявок от заказчиков. Заказы выполняют 5 мастеров, каждый из которых затрачивает в среднем на выполнение одного заказа 12 дней. Определить загруженность мастеров и процесс выполнения заказов.

Математическая модель такой системы следующая. Система многоканальная (s=5), интенсивность поступления заявок =10, интенсивность одного канала обслуживания . Поскольку все мастера работают с одинаковой интенсивностью, то общая интенсивность всей бригады мастеров =2,5. Длина очереди не ограничена – заявок может быть сколько угодно.

Требуется определить:

• вероятность того, что все мастера свободны Р₀;

• вероятность того, что все мастера заняты и имеется очередь Р;

• среднее время ожидания заявки в очереди и в обслуживании ;

• среднюю длину очереди на обслуживание ;

• среднее число заявок в системе обслуживания ;

• среднее время пребывания заявки в системе ;

Коэффициент загрузки системы

.

Вероятность того, что все мастера заняты:

.

Среднее время нахождения заявки в очереди на обслуживание:

дней.

Средняя длина очереди

заказчиков.

Для определения среднего числа заявок необходимо определить вероятность того, что в системе находится ровно 5 заявок

.

Среднее число заявок в системе обслуживания

заказчиков.

Комбинат работает не плохо. Хотя средняя длина очереди не маленькая – 11 заказчиков, однако, выполненный заказ можно получить довольно быстро – через 19 дней после подачи заказа. Это время можно несколько уменьшит, если будут работать 6 мастеров.

Вопросы для самопроверки.

1. Что значит описать физическую и математическую СМО?

2. Чем характеризуется входной поток СМО?

3. Чем характеризуется дисциплина очереди СМО?

4. Что значит задать математически механизм обслуживания?

5. Для чего используется такая характеристика как состояние СМО?

6. Какие показатели характеризуются СМО?

7. Что предопределяют вероятности нахождения СМО в определенном состоянии?

8. Как определить среднее время обслуживание механизма обслуживания, имеющего различную структуру?

9. Почему различные расчетные формулы для многоканальной и одноканальной СМО?

10. Почему различные расчетные формулы для СМО с конечным числом состояний и неопределенным числом состояний?